A wire loop enclosing as semicircle of radius R is located on the boudary of uniform magnetic field B. At the moment t=0, the loop is set into rotation with a costant angular acceleration α about an axis O coinciding with a line of vector B on the boundary. Find the emf induced in the loop as a function of time. Draw the approximate plot of this function.The arrow in the figure shows the emf direction taken to be positive.
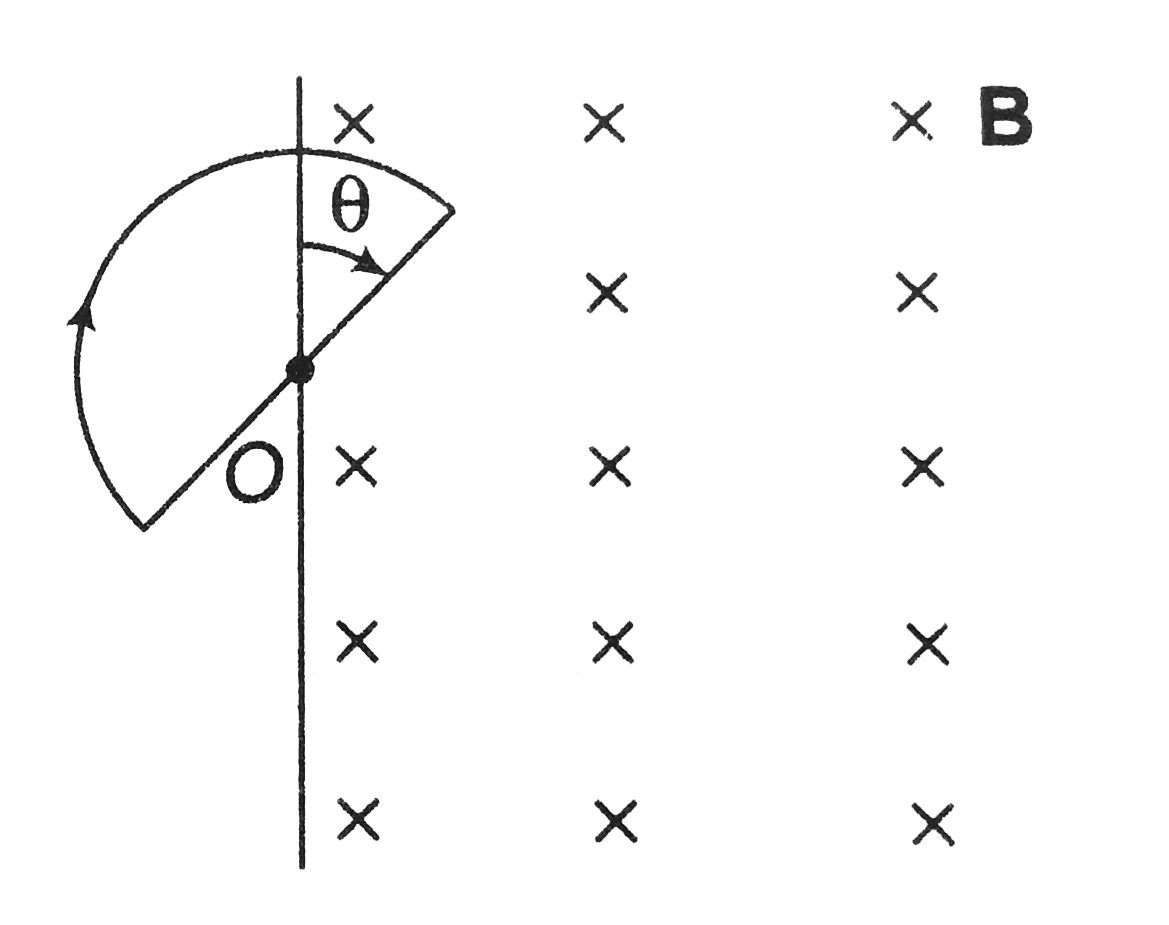
θ=12at2
∴t=√2θα= time taken to rotate angleθ
where θ=0, to π,2π to 3π,4π to 5π etc.
⊗ magnetic field passing through the loop is increasing. Hence, current in the loop is anti clockwise or induced emf is negative. And for θ=π to 2π,3π→3π,5π→6π etc.
⊗ magnetic field passing through the loop is decresing.Hence, current in the loop is clockwise or emf is positive.
So,
t1= time taken to rotate an angle π=√2πα
t2= time taken to rotate an angle 2π=√4πα
... ... ... ... ...
tn=time taken to rotate an angle nπ=√2nπα
Now, from 0 to t1 emf is negative
t1 to t2 is positive
t2 to t3 emf is again negative
and so on.
Now, at time t, angle rotated us θ=12αt2
Area inside the filed is S=(πR)2(θ2π)=12R2θ
or S=14R2αt2
So, flux passing through the loop, ϕ=BS=14BR2αt2
e=∣∣∣dϕdt∣∣∣=12BR2αt
e∝t
i.e. e−t graph is a staright line passing through origin. e−t equation wih sign can be written as
e=(−1)n(12BR2αt)
Here, n=1,2,3.. is the number of half revolutions that the loop performs at the given moment t.
The e−t graph is as shown in figure.

Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.1
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.2
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 6
3 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A wire loop enclosing a semicircle of radius R islocated on the boundary of a uniform magnetic field B. At the moment t=0, the loop is set into rotation with constant angular acceleration α about an axis O. The clockwise emf direction is taken to be positive.

The variation of emf as a function of time is
View SolutionA wire loop enclosing a semicircle of radius R islocated on the boundary of a uniform magnetic field B. At the moment t=0, the loop is set into rotation with constant angular acceleration α about an axis O. The clockwise emf direction is taken to be positive.
The variation of emf as function of time is
View SolutionA wire loop enclosing a semi-circle of radius a=2cm is located on the boundary of a uniform magnetic field of induction B=1T (figure).At the moment t=0 the loop is set into rotation with a constant angular acceleration β=2rad/sec2 about an axis O coinciding with a line of vector B on the boundary.The emf induced in the loop as a function of time t is [x×10−4(−1)n×t]V, where n=1,2,... is the number of the half-revolution taht the loop performs at the given moment t.Find the value of x.(The arrow in the figure shows the emf direction taken to be positive, at t=0 loop was completely outside)

View SolutionA semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
View SolutionA metallic loop is placed in a nonuniform magnetic field. Will an emf be induced in the loop?
View SolutionA wire loop confined in a plane is rotated in its open plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA current I flows along a round circular loop of radius R. Find the line integration of magnetic field along the axis of the loop from center to ∞
View SolutionA circular wire loop of radius r is placed in a region of uniform magnetic field B such that the plane of the loop makes an angle θ with the direction of B. In which of the following conditions, will no emf be induced in the loop?
View SolutionA wire bent as a parabola y=kx2 is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0, the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -
View Solution
