A cricket fielder can throw the cricket ball with a speed v0. If he throws the ball while running with speed (u) at angle θ to the horizontal, find
(b) what will be time of flight ?
(c ) what is the distance (horizontal range) form the point of projection at which the ball will land ?
(d) find θ at which he should throw the ball that would maxmise the horizontal range range as found in (c ).
(e) how does θ for maximum range change if u gt v_0, u=v_0, ult v_0 ?
(f) how does θ in (e) compare with that for u=0 (i.e., 45^@) ?
Consider the adjacent diagram.
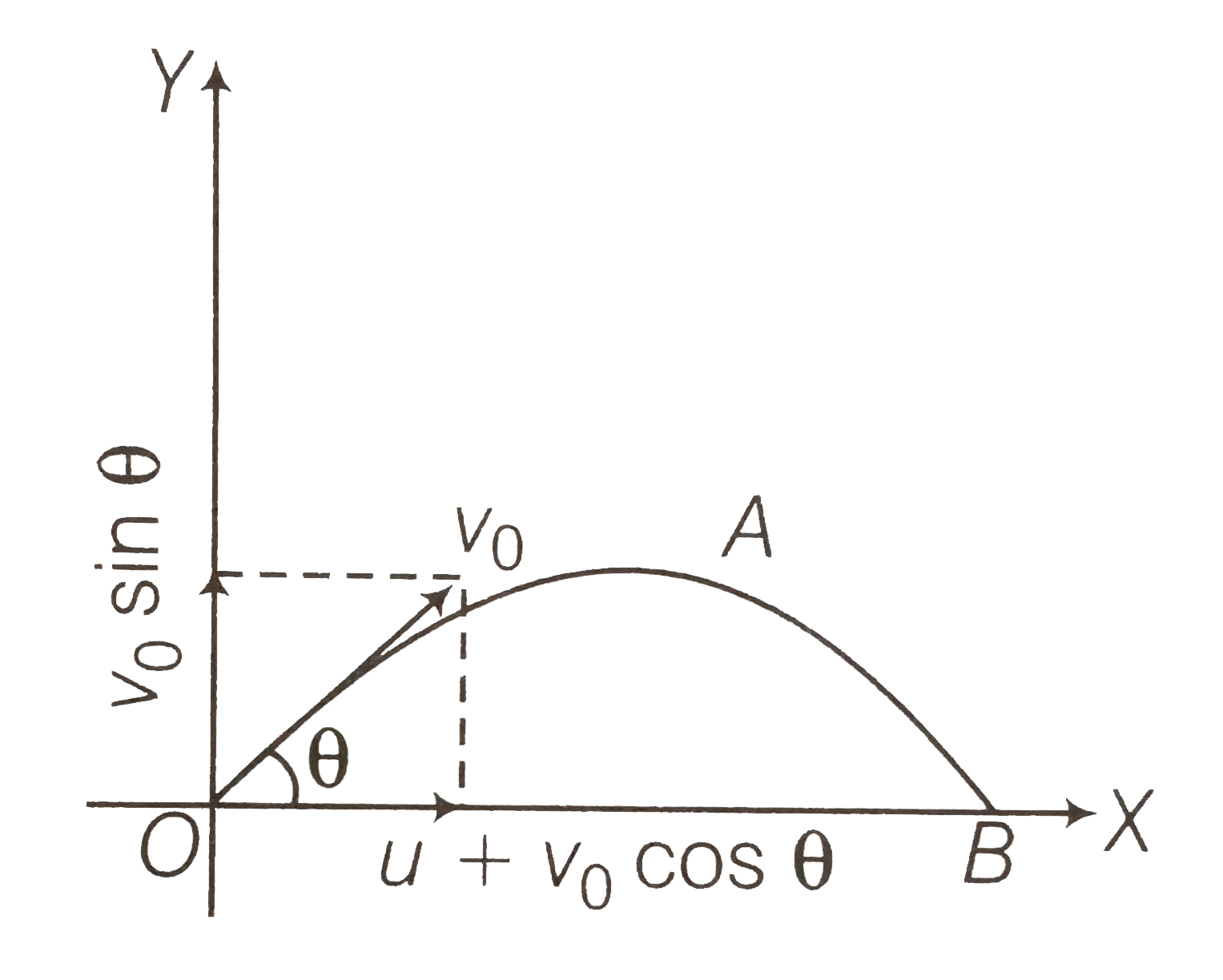
(a) Initial velocity in
x-direction , ux=u+v0cosθ
uy=Initial velocity in Y - direction
=v0sinθ
where angle of projection is θ.
Now, we can write
tanθ=uyux=u0sinθu+u0cosθ
⇒ θ=tan−1(v0sinθu+v0cosθ)
(b) Let T be the time of flight.
As net displacement is zero over time period T.
y=0,uy=v0sinθ,ay=−g,t=T
We know that y=uyt+12ayt2
⇒ 0=v0sinθT+12(−g)T2
⇒ T[v0sinθ−g2T]=0⇒T=0,2v0sinθg
T=01, corresponds to point O.
Hence, T=2u0sinθg
(c) Horizontal range ,R=(u+v0cosθ)T=(u+v0cosθ)2v0sinθg
=v0g[2usinθ+v0sin2θ]
(d) For horizontal range to be maximum, dRdθ=0
⇒ v0g[2ucosθ+v0cos2θ×2]=0
⇒ 2ucosθ+2v0[2cos2θ−1]=0
⇒ 4v0cos2θ+2ucosθ−2v0=0
⇒ 2v0cos2θ+ucosθ−v0=0
⇒ cosθ=−u±√u2+8v204v0
⇒ θmax=cos−1⎡⎢
⎢⎣−u±√u2+8v204v0⎤⎥
⎥⎦
=cos−1⎡⎢
⎢⎣−u±√u2+8v204v0⎤⎥
⎥⎦
(e) If u=v0,
cosθ=−v0±√v20+8v204v0=−1+34=12
⇒ θ=60∘
Ifu<<v0,then 8v20+u2≈8v20
θmax=cos−1[−u±2√2v04v0]=cos−1[1√2−u4v0]
If u<<v0,then θmax=cos−1(1√2)=π4
Ifu>u0 and u>>v0
θmax=cos−1[−u±u4v0]=0⇒θmax=π2
(f) Ifu=0,θmax=cos−1[0±√8v204v0]=cos−1(1√2)=45∘
Topper's Solved these Questions
Similar Questions
A cricket fielder can throw the cricket ball with a speed v0. If the throws the ball while running with speed u at an angle θ to the horizontal,
View SolutionA cricket fielder can throw the cricket ball with a speed v0.If the throws the ball while running with speed u at an angle θ to the horizontal.
The effective angle to the horizontal at which the ball is projected in air as seen by a spectator is
View Solution
Knowledge Check
A cricket fielder can throw the cricket ball with a speed v0.If the throws the ball while running with speed u at an angle θ to the horizontal.
The effective angle to the horizontal at which the ball is projected in air as seen by a spector isAθ=tan−1(v0sinθu+v0cosθ)Bθ=tan−1(v0cosθu+v0sinθ)Cθ=cot−1(v0cosθu+v0sinθ)Dθ=cot−1(v0cosθu+v0sinθ)A ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
A2v2gB√2[2v2g]Cv2gD√2v2gThe angle in which a cricket ball should be hit to travel maximum horizontal distance is
A60∘ with horizontalB45∘ with horizontalC30∘ horizontalD15∘ with horizontal
A ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA ball is projected with initial speed u at an angle θ above the horizontal . Calculate the time after which ball will be moving at right angle to its initial velocity.
View SolutionA ball is projected with velocity (u) at an anle α with horizontal plane. What is its speed when it makes an angle θ whith the horizontal plane ?
View SolutionA bowler throws a cricket ball at a speed of 120 km/h. How long does this ball take to travel a distance of 20 metres to reach the batsman?
View SolutionA ball is projected at an angle 60∘ with the horizontal with speed 30 m/s. What will be the speed of the ball when it makes an angle 45∘ with the horizontal ?
View Solution
