A cube of side b has a charge q at each of its vertices. Determine the electric field due to this charge array at the center of the cube.
q/b2
q/2b2
32q/b2
zero
The correct Answer is:D
To determine the electric field at the center of a cube with a charge q at each of its vertices, we can follow these steps:
1. Understand the Geometry of the Cube:
- A cube has 8 vertices, and we have a charge q located at each vertex.
- The side length of the cube is given as b.
2. Identify the Center of the Cube:
- The center of the cube can be found at the coordinates (b2,b2,b2).
3. Calculate the Distance from the Center to a Vertex:
- The distance r from the center of the cube to any vertex can be calculated using the Pythagorean theorem:
r=√(b2)2+(b2)2+(b2)2=√3b24=b√32
4. Determine the Electric Field due to a Single Charge:
- The electric field E due to a single charge q at a distance r is given by:
E=k⋅qr2
- Substituting for r:
E=k⋅q(b√32)2=k⋅q3b24=4kq3b2
5. Direction of the Electric Field:
- The electric field due to each charge points away from the charge if it is positive.
- For each pair of opposite charges, the electric fields will have components that cancel each other out due to symmetry.
6. Analyze the Contribution of All Charges:
- Since there are 8 charges symmetrically placed at the vertices, the contributions to the electric field from opposite pairs will cancel out.
- For every charge at a vertex, there is an equal and opposite charge at the diagonally opposite vertex, leading to cancellation of the electric fields.
7. Conclusion:
- The net electric field at the center of the cube due to all the charges at the vertices is:
Enet=0
Final Answer:
The electric field at the center of the cube is zero.
- A cube has 8 vertices, and we have a charge q located at each vertex.
- The side length of the cube is given as b.
- The center of the cube can be found at the coordinates (b2,b2,b2).
- The distance r from the center of the cube to any vertex can be calculated using the Pythagorean theorem:
r=√(b2)2+(b2)2+(b2)2=√3b24=b√32
- The electric field E due to a single charge q at a distance r is given by:
E=k⋅qr2
- Substituting for r:
E=k⋅q(b√32)2=k⋅q3b24=4kq3b2
- The electric field due to each charge points away from the charge if it is positive.
- For each pair of opposite charges, the electric fields will have components that cancel each other out due to symmetry.
- Since there are 8 charges symmetrically placed at the vertices, the contributions to the electric field from opposite pairs will cancel out.
- For every charge at a vertex, there is an equal and opposite charge at the diagonally opposite vertex, leading to cancellation of the electric fields.
- The net electric field at the center of the cube due to all the charges at the vertices is:
Enet=0
The electric field at the center of the cube is zero.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.2
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View Solution
Knowledge Check
A cube of side x has a charge q at each of its vertices. Determine the potential due to this charge array at the center of the cube.
A4q3πε0xB4q√3πε0xC3q4πε0xD2q√3πε0xA hexagon of side 8 cm has a charge 4μC at each of its vertices. The potential at the centre of the hexagon is
A2.7×106VB7.2×1011VC2.5×1012VD3.4×104V
Given a cube with point charges q on each of its vertices. Calculate the force exerted on any of the charges due to rest of the 7 charges.
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
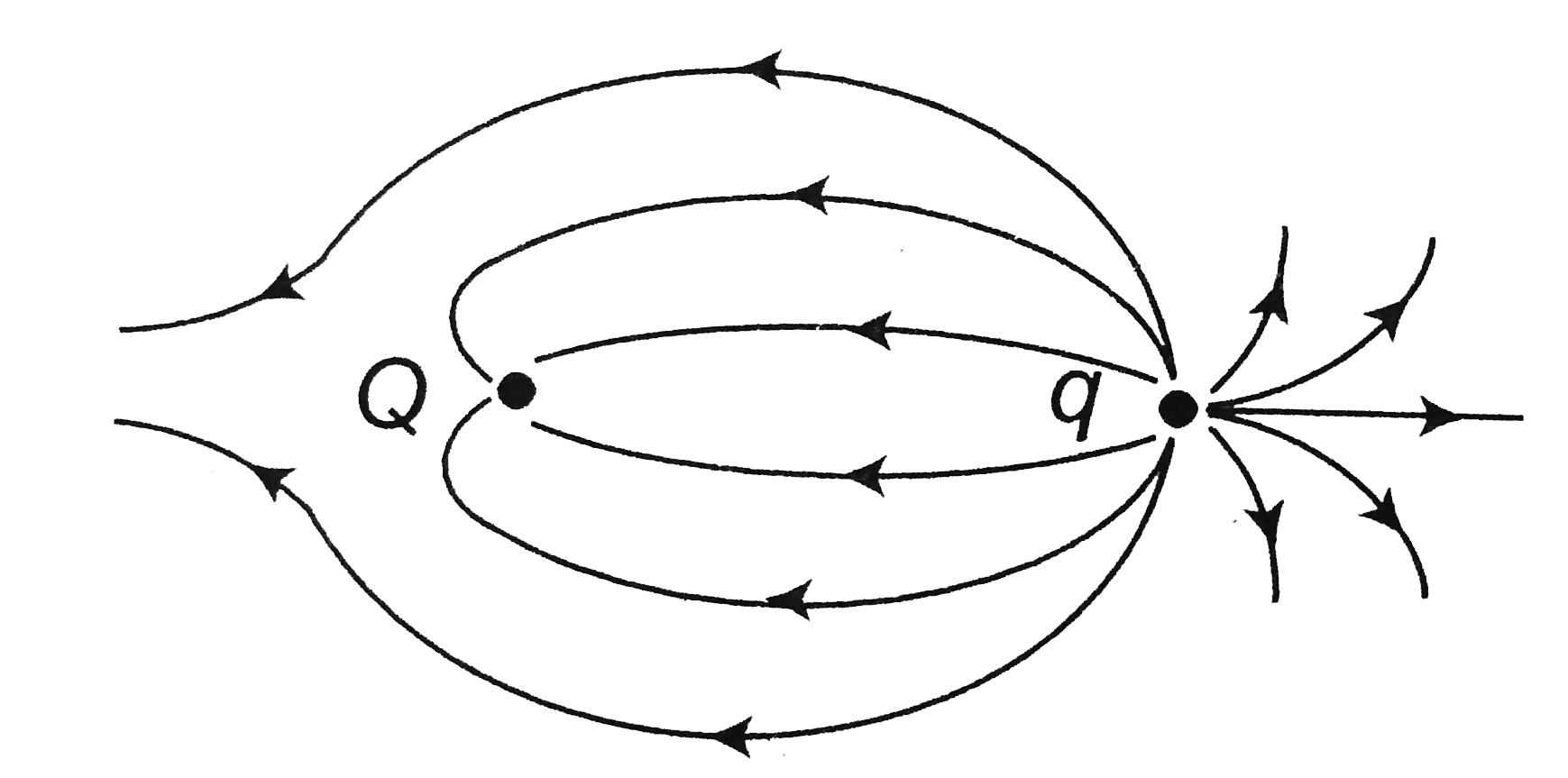
View SolutionThe lines of force of the electric field due to two charges q and Q are sketched in the figure. State if
View SolutionA charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
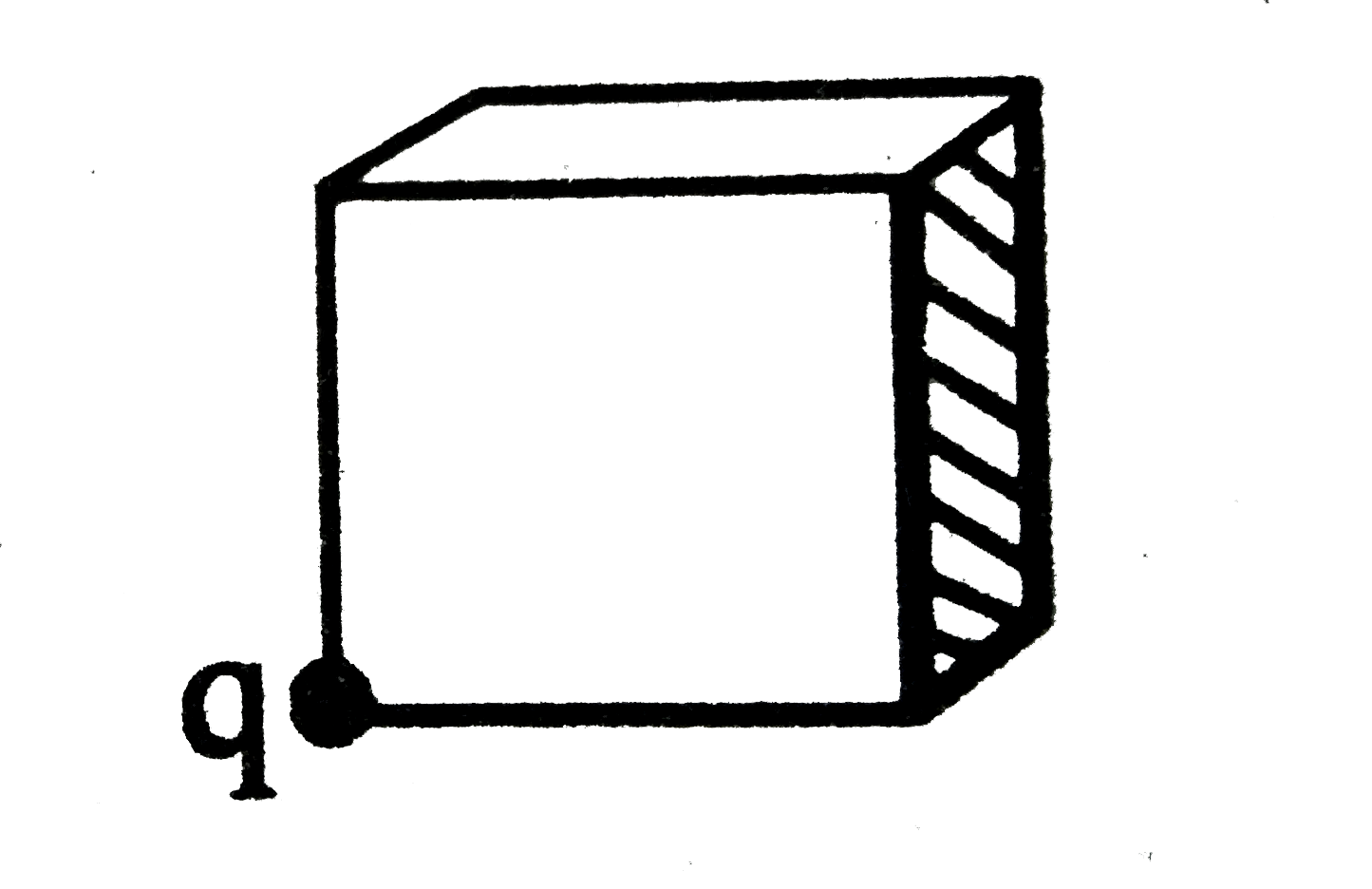
View SolutionThe length of each side of a cubical closed surface is l If charge q is situated on one of the vertices of the cube , then find the electric flux passing through shaded face of the cube.
 .
.
View SolutionWhen identical point charges are placed at the vertices of a cube of edge length 'a' each of them experiences a net force of magnitude F.
Now these charges are placed on the vertices of another cube of edge length 'b'. What will be magnitude of the net force on any of the charges? These cubes are simply geometrical constructs and not made by any matter.
View Solution
