A cubical vessel (open from top) of side L is filled with a liquid of density ρ.
What is the torque of hydrostatic force on a side wall about an axis passing through one of the bottom edges?
ρgL44
ρgL46
2ρgL43
ρgL43
The correct Answer is:B
To find the torque of the hydrostatic force on a side wall of a cubical vessel about an axis passing through one of the bottom edges, we can follow these steps:
1. Define the Problem:
We have a cubical vessel of side length L filled with a liquid of density ρ. We need to calculate the torque about an axis at one of the bottom edges of the side wall.
2. Consider an Element of the Wall:
At a depth x from the top of the liquid, consider a thin horizontal strip of thickness dx on the side wall. The area of this strip is:
dA=L⋅dx
3. Calculate the Pressure at Depth x:
The pressure at this depth due to the liquid is given by:
P=ρgx
where g is the acceleration due to gravity.
4. Determine the Hydrostatic Force on the Strip:
The hydrostatic force dF acting on the strip is given by:
dF=P⋅dA=ρgx⋅(L⋅dx)=ρgLxdx
5. Calculate the Distance from the Axis of Rotation:
The distance from the axis (bottom edge) to the strip at depth x is:
r=L−x
6. Find the Torque Contribution from the Strip:
The torque dτ due to the force dF about the axis is:
dτ=dF⋅r=(ρgLxdx)⋅(L−x)=ρgLx(L−x)dx
7. Integrate to Find Total Torque:
To find the total torque τ, integrate dτ from x=0 to x=L:
τ=∫L0ρgLx(L−x)dx
8. Simplify the Integral:
Expanding the integrand:
τ=ρgL∫L0(Lx−x2)dx
Now, calculate the integral:
∫L0Lxdx=L⋅x22∣∣∣L0=L⋅L22=L32
∫L0x2dx=x33∣∣∣L0=L33
Thus,
τ=ρgL(L32−L33)
9. Combine the Results:
Finding a common denominator (6):
τ=ρgL(3L36−2L36)=ρgL⋅L36=ρgL46
Final Result:
The torque of the hydrostatic force on a side wall about an axis passing through one of the bottom edges is:
τ=ρgL46Newton meter
We have a cubical vessel of side length L filled with a liquid of density ρ. We need to calculate the torque about an axis at one of the bottom edges of the side wall.
At a depth x from the top of the liquid, consider a thin horizontal strip of thickness dx on the side wall. The area of this strip is:
dA=L⋅dx
The pressure at this depth due to the liquid is given by:
P=ρgx
where g is the acceleration due to gravity.
The hydrostatic force dF acting on the strip is given by:
dF=P⋅dA=ρgx⋅(L⋅dx)=ρgLxdx
The distance from the axis (bottom edge) to the strip at depth x is:
r=L−x
The torque dτ due to the force dF about the axis is:
dτ=dF⋅r=(ρgLxdx)⋅(L−x)=ρgLx(L−x)dx
To find the total torque τ, integrate dτ from x=0 to x=L:
τ=∫L0ρgLx(L−x)dx
Expanding the integrand:
τ=ρgL∫L0(Lx−x2)dx
Now, calculate the integral:
∫L0Lxdx=L⋅x22∣∣∣L0=L⋅L22=L32
∫L0x2dx=x33∣∣∣L0=L33
Thus,
τ=ρgL(L32−L33)
Finding a common denominator (6):
τ=ρgL(3L36−2L36)=ρgL⋅L36=ρgL46
The torque of the hydrostatic force on a side wall about an axis passing through one of the bottom edges is:
τ=ρgL46Newton meter
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Matrix Matching12videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct21videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.14videos
RAY OPTICS
Similar Questions
A cubical vessel (open from top) of side L is filled with a liquid of density ρ.
What is the ratio of magnitude of torque on one side wall to the torque on base about the same axisView SolutionA small solid ball of density ρ is held inside at point A of a cubical container of side L, filled with an ideal liquid of density 4ρ as shown in the figure. Now, if the container starts moving with constant acceleration a horizontally and the ball is released from point A simultaneously, then choose from following the correct option(s)
 View Solution
View SolutionThe moment of inertia of a hollow cubical box of mass M and side a about an axis passing through the centres of two opposite faces is equal to.
View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The graph of the pressure gradient (dPdx) with the distance x meaured from the axis of rotation is :View SolutionFour point masses, each of mass m, are fixed at the corners of a square of side l. The square is rotating with angular frequency ω, about an axis passing through one of the corners of the square and parallel to its diagonal , as shown. Angular momentum about this axis is :
 View Solution
View SolutionPassage-I :
A hollow cube of side L has two parallel sides conducting and remaining four sides are non conducting. It is filled with a liquid of dielectric constant K. A small hole of area A at bottom of cube is open at t = 0 and liquid starts leaking throught it. The two conducting sides are connected by a battery of emf E (L=9mA=18√20m2k=10E=81v,g=10m/sec)

Current through the connecting wire of a time is given byView SolutionPassage-I :
A hollow cube of side L has two parallel sides conducting and remaining four sides are non conducting. It is filled with a liquid of dielectric constant K. A small hole of area A at bottom of cube is open at t = 0 and liquid starts leaking throught it. The two conducting sides are connected by a battery of emf E (L=9mA=18√20m2k=10E=81v,g=10m/sec)

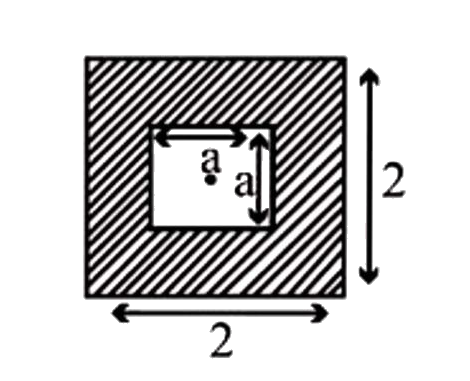
Capacitance of capacitor as a function of timeView SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
 View Solution
View Solution

