Four point masses, each of mass m, are fixed at the corners of a square of side l. The square is rotating with angular frequency ω, about an axis passing through one of the corners of the square and parallel to its diagonal , as shown. Angular momentum about this axis is :

ml2ω
ml2ω
3ml2ω
2ml2ω
Step by step video & image solution for Four point masses, each of mass m, are fixed at the corners of a square of side l. The square is rotating with angular frequency omega, about an axis passing through one of the corners of the square and parallel to its diagonal , as shown. Angular momentum about this axis is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
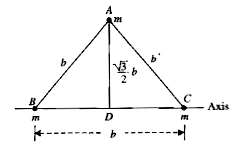 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
Four point masses each of mass 'm' are placed on the corner of square of side 'a' Calculate magnitude of gravitational force experienced each particle
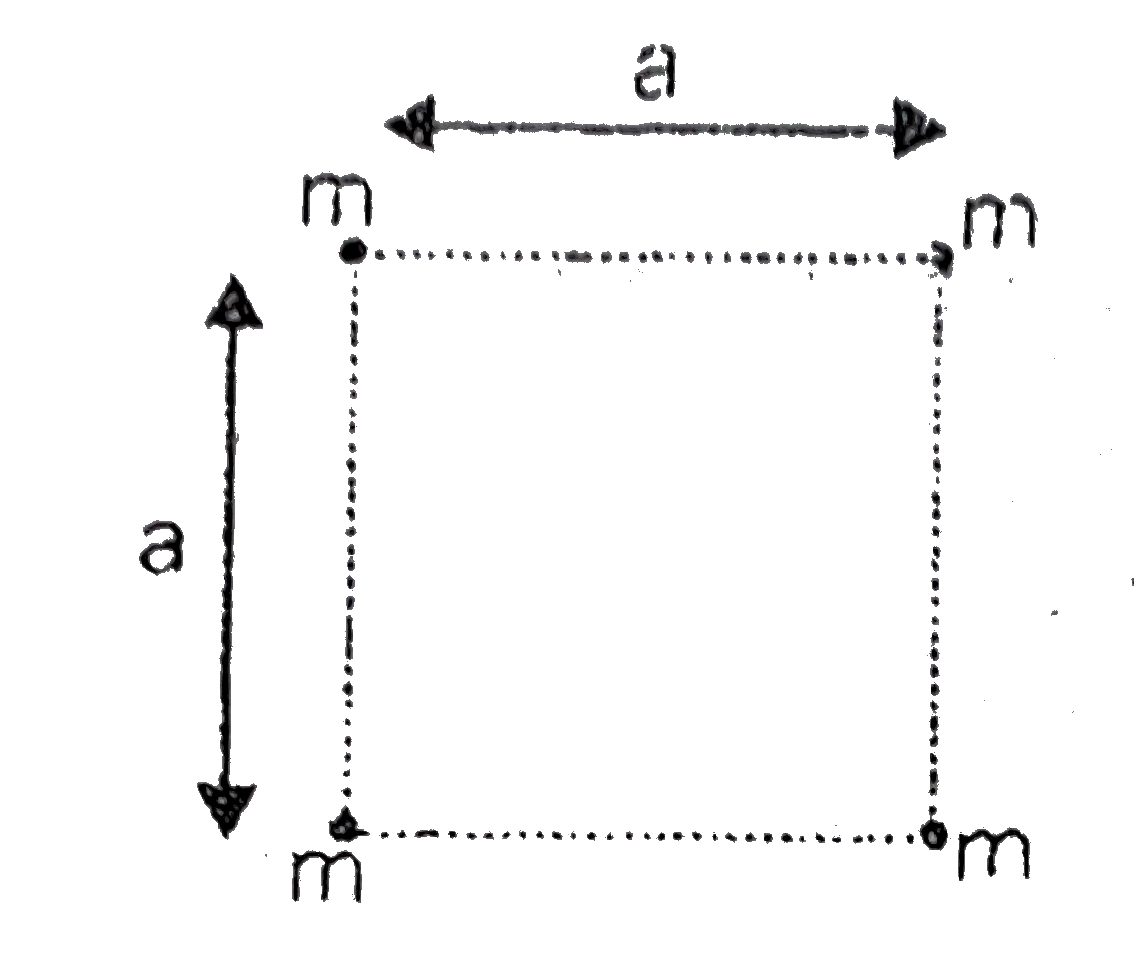 .
.
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.

View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionFour spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then moment of inertia of the system about an axis about one of the sides of the square is :-
View SolutionThree masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View Solution

