A current i1=i0sinωt passes through a resistor of resistance R. How much thermal energy is produced in one time period? A current i2=−i0sinωt passes through the resistor. How much thermal energy is produced in one time period? If i1andi2 both pass through the resistor simultaneously, how much thermal energy is produced? Is the principle of superposition obeyed in this case?
To solve the problem step by step, we will analyze the thermal energy produced by the currents i1 and i2 passing through a resistor R over one time period T.
Step 1: Calculate Thermal Energy for i1
1. The current i1 is given by i1=i0sin(ωt).
2. The root mean square (RMS) value of the current i1 is calculated as:
Irms=i0√2
3. The formula for thermal energy H produced in one time period T is:
H=I2rms⋅R⋅T
where T=2πω (the time period).
4. Substituting Irms and T:
H=(i0√2)2⋅R⋅2πω
5. Simplifying this gives:
H=i202⋅R⋅2πω=πi20Rω
Step 2: Calculate Thermal Energy for i2
1. The current i2 is given by i2=−i0sin(ωt).
2. The RMS value of the current i2 is the same as i1:
Irms=i0√2
3. The thermal energy produced by i2 over one time period is calculated similarly:
H=I2rms⋅R⋅T
4. Substituting the values gives:
H=πi20Rω
Step 3: Calculate Total Thermal Energy for i1 and i2 Simultaneously
1. When both currents i1 and i2 pass through the resistor simultaneously, the total current i is:
i=i1+i2=i0sin(ωt)−i0sin(ωt)=0
2. Since the total current is zero, no thermal energy is produced:
Htotal=0
Step 4: Check the Principle of Superposition
1. The principle of superposition states that the total response (thermal energy in this case) in a linear system is the sum of the responses from each individual input.
2. In this case, while Hi1 and Hi2 are equal, their effects cancel each other out when combined, resulting in zero thermal energy.
3. Thus, the principle of superposition is obeyed, as the total energy produced (0) is indeed the sum of the individual energies (both equal but opposite).
Final Answers
1. Thermal energy produced by i1: H=πi20Rω
2. Thermal energy produced by i2: H=πi20Rω
3. Total thermal energy when both currents are present: Htotal=0
4. The principle of superposition is obeyed in this case.
2. The root mean square (RMS) value of the current i1 is calculated as:
Irms=i0√2
3. The formula for thermal energy H produced in one time period T is:
H=I2rms⋅R⋅T
where T=2πω (the time period).
4. Substituting Irms and T:
H=(i0√2)2⋅R⋅2πω
5. Simplifying this gives:
H=i202⋅R⋅2πω=πi20Rω
2. The RMS value of the current i2 is the same as i1:
Irms=i0√2
3. The thermal energy produced by i2 over one time period is calculated similarly:
H=I2rms⋅R⋅T
4. Substituting the values gives:
H=πi20Rω
i=i1+i2=i0sin(ωt)−i0sin(ωt)=0
2. Since the total current is zero, no thermal energy is produced:
Htotal=0
2. In this case, while Hi1 and Hi2 are equal, their effects cancel each other out when combined, resulting in zero thermal energy.
3. Thus, the principle of superposition is obeyed, as the total energy produced (0) is indeed the sum of the individual energies (both equal but opposite).
2. Thermal energy produced by i2: H=πi20Rω
3. Total thermal energy when both currents are present: Htotal=0
4. The principle of superposition is obeyed in this case.
Topper's Solved these Questions
Similar Questions
A current of 2 A is passed through a coil of resistance 75 ohm for 2 minutes
How much heat energy is produced ?
View SolutionAn electric current of 2.0 A passes through a wire of resistance 25Ω. How much heat will be developed in 1 minute?
View SolutionAn electric current of 2.0 A passes through a wire of resistance 25Ω. How much heat will be developed in 1 minute?
View SolutionA current of 2 A is passed through a coil of resistance 75 ohm for 2 minutes
How much charge is passed through the resistance ?
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionA sinusoidal ac current flows through a resistor of resistance R . If the peak current is Ip , then the power dissipated is
View SolutionA 10 V storage battery of negligible internal resistance is connected across a 50Ω resistor. How much heat energy is produced in the resistor in 1 hour
View SolutionThe current I1 ( in A ) flowing through 1 Ω resistor in the following circuit is :
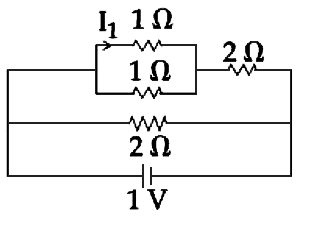
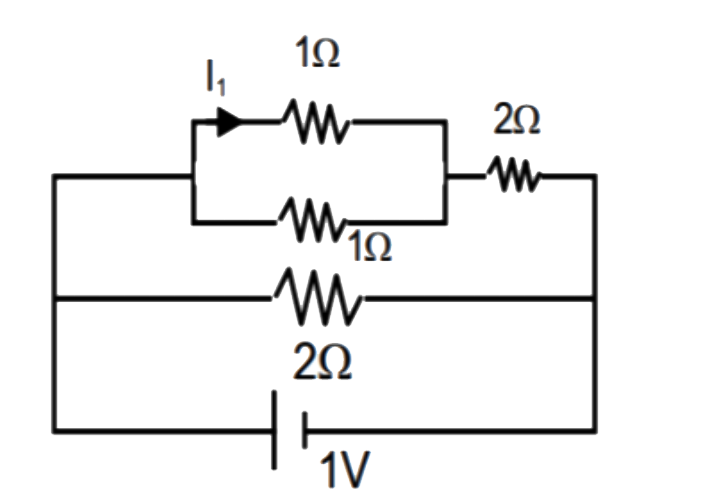
View SolutionThe current I1 (in A) flowing through the 1Ω resistor in the given circuit is
View SolutionHow much chlorine will be liberated on passing one ampere current for 30 minutes through NaCl solution ?
View Solution
