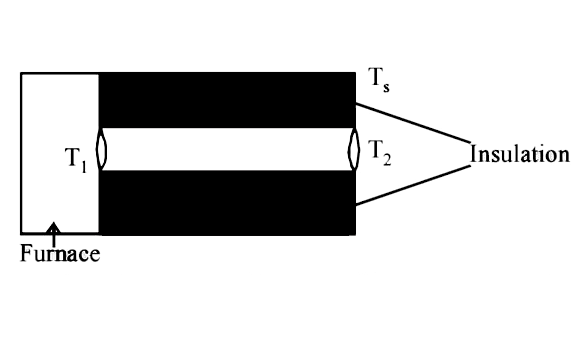
A cylinder rod of length 1, thermal conductivity K and area of cross section A has one end in the furnace at temperature T1 and the other end in surrounding at temperature T2. Surface of the rod exposed to the surrounding has emissivity e. Also T2=Ts+ΔTandTs>>ΔT. If T1−Ts∝ΔT,find the proportionality constant.
The correct Answer is:A, C, D
From the figure is clear that emission takes place form the
surface at temperature T2(circular cross section). Heat
conduction and radiation through lateral surface is zero.
Heat conducted through rod is
Q=KA(T1−T2)Δtl
Energy emitted by surface of rod in same time Δt, is
E=eσA(T42−T4s)Δt
Since rod is at thermal equilibrium therefore E=Q
hence, KA(T1−T2)Δtl=eσA(T42−T4s)Δt
⇒T1−T2=eσA(T42−T4s)lK
Here T2−Ts=ΔTandTs>>ΔT
T1−(ΔT+Ts)=eσlK[(ΔT+Ts)4−T4s]
T1−(ΔT+Ts)=eσlK×T4s[(1+ΔTTs)4−1]
(ΔT+Ts)=eσlK×T4s[1+4ΔTTs−1]
or T1−(Ts+ΔT)=4eσlKT3sΔT
or T1−Ts=(4eσlT3sK+1)ΔT
∴The∝ortionalityconstant=(1+4eσlT3sK)
Topper's Solved these Questions
Similar Questions
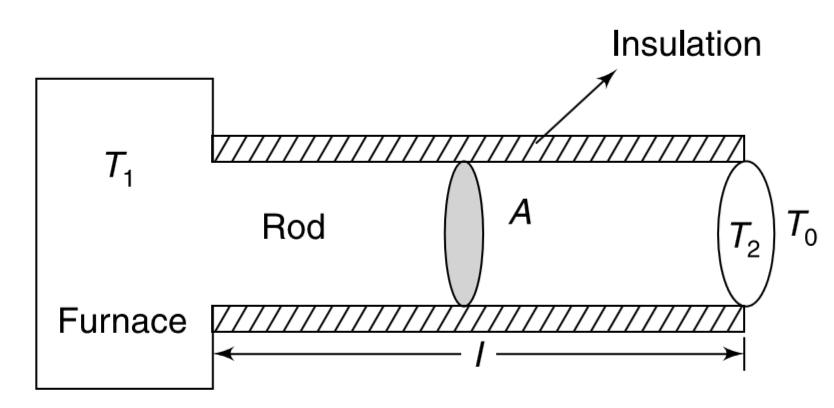
A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
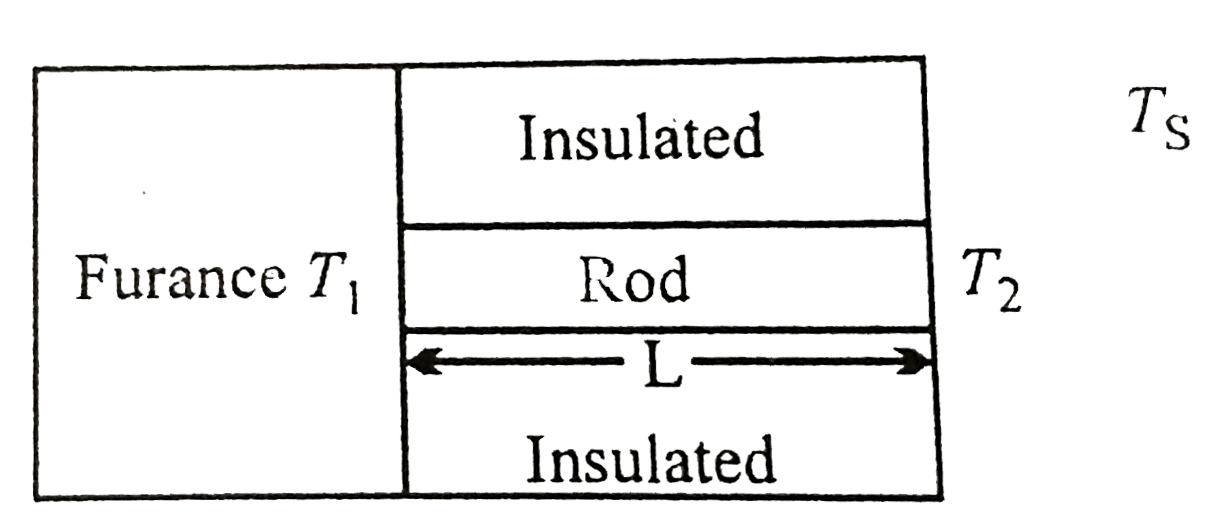
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
View Solution
Knowledge Check
Consider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
AK1A1=K2A2BK2A1=K1A2CK1A1S1=K2A2S2DK2A1S2=K1A2S1If K1 is the equilibrium constant at temperature T1andK2 is the equilibrium constant at temperature T2and If T2>T1 and reaction is endothermic then
AK2<K1BK2=K1CK2>K1DAll of theseAll the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?
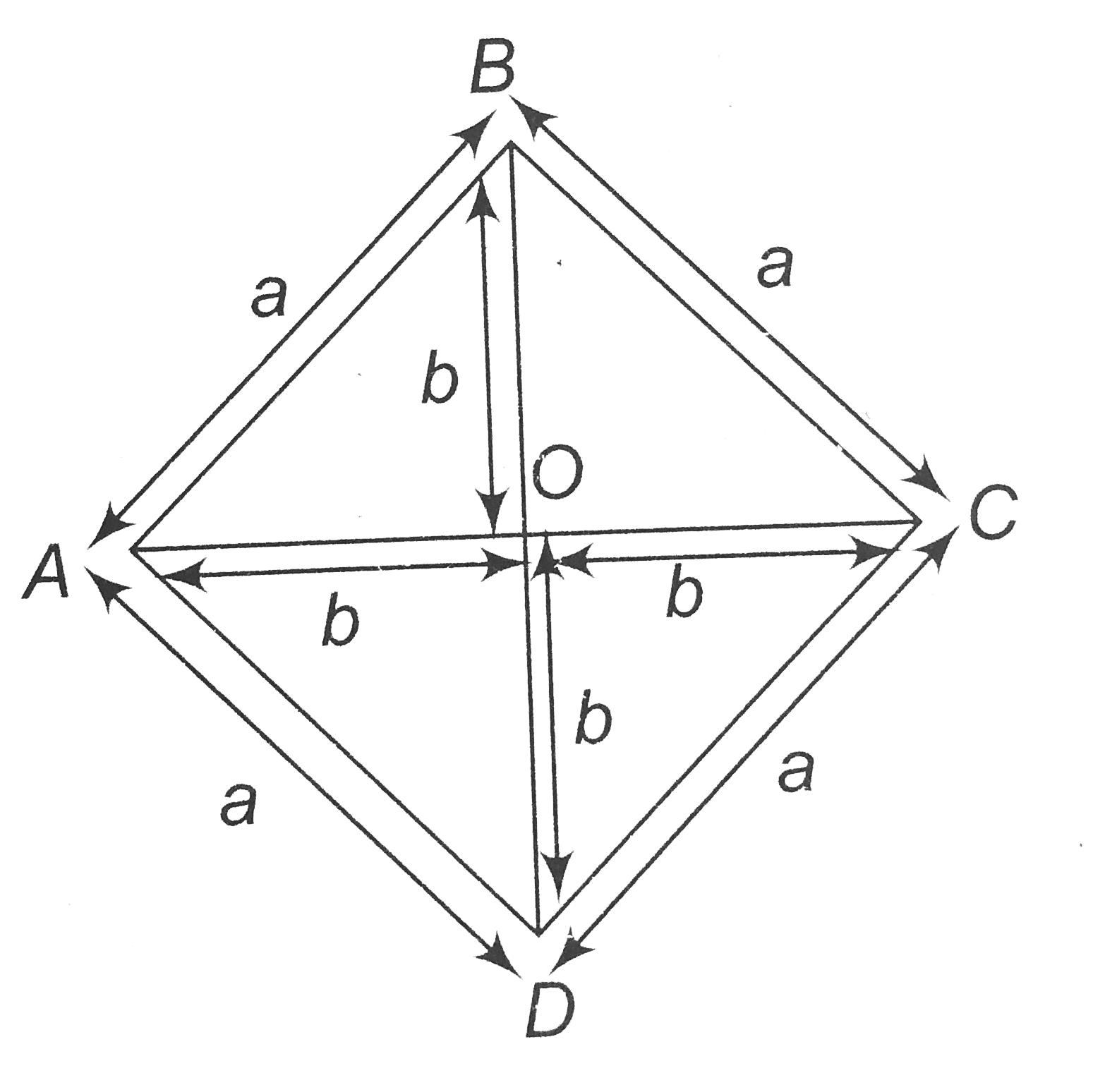 ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
A uniform rod of thermal conductivity of 65J/m−s−∘C is surrounded by an insulator on its sides. One of its ends is put in a furnace, while the other end is kept exposed. If the temperature gradient of the rod is −75∘C/m, find the emissive power of the exposed end.
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
View SolutionCondider two rods of same length and different specific heats (s1,s2), thermal conductivities (K1,K2) and areas of cross-section (A1,A2) and both having temperatures (T1,T2) at their ends. If their rate of loss of heat due to conduction are equal, then
View SolutionThe efficiency of an ideal heat engine working between the temperatureT1 and T2(T1>T2) is
View Solution
