A cylinder rotating with angular velocity ω0 is put on a rough horizontal floor so that edge touches a vertical rough wall. Rotational motion of the cylinder is retarded and after some time cylinder comes to rest. If m is mass of cylinder and R is its radius then calculate number of revolutions made by the cylinder before it comes to rest. Assume μ is coefficient of friction for floor as well as wall.
To solve the problem of a rotating cylinder coming to rest due to friction, we can follow these steps:
Step 1: Identify Forces Acting on the Cylinder
The cylinder experiences gravitational force mg downward, normal forces n1 (from the floor) and n2 (from the wall), and frictional forces f1 (from the floor) and f2 (from the wall).
Step 2: Set Up Equations for Forces
1. Vertical Forces: The sum of vertical forces must equal zero.
n1+f2−mg=0(1)
Rearranging gives:
n1+f2=mg
2. Horizontal Forces: The sum of horizontal forces must also equal zero.
f1−n2=0(2)
This implies:
f1=n2
Step 3: Express Frictional Forces in Terms of Normal Forces
Using the coefficient of friction μ:
- The frictional force from the floor:
f1=μn1
- The frictional force from the wall:
f2=μn2
Step 4: Substitute Frictional Forces into the Equations
Substituting f2 into equation (1):
n1+μn2=mg
Substituting n2 from equation (2):
n1+μf1=mg
Since f1=μn1:
n1+μ2n1=mg
Factoring out n1:
n1(1+μ2)=mg
Thus,
n1=mg1+μ2
Step 5: Calculate n2
Now substituting n1 back to find n2:
n2=μn1=μmg1+μ2
Step 6: Calculate the Work Done by Friction
The work done by the friction forces is equal to the change in kinetic energy:
Work=−f1Rθ−f2Rθ=−Rθ(f1+f2)
Substituting f1 and f2:
=−Rθ(μn1+μn2)=−Rθ(μmg1+μ2+μ2mg1+μ2)
This simplifies to:
=−Rθ⋅μmg(1+μ2)1+μ2=−μmgRθ
Step 7: Relate Work Done to Change in Kinetic Energy
The initial kinetic energy of the cylinder is:
KEi=12Iω20=12⋅12mR2ω20=mR2ω204
The final kinetic energy is zero when the cylinder comes to rest:
Work=ΔKE=KEf−KEi=0−mR2ω204
Setting the work done equal to the change in kinetic energy:
−μmgRθ=−mR2ω204
Step 8: Solve for θ
Canceling m and rearranging gives:
θ=Rω204μg
Step 9: Calculate the Number of Revolutions
Since θ is in radians, the number of revolutions n is given by:
n=θ2π=Rω204μg⋅2π=Rω208πμg
Final Answer
The number of revolutions made by the cylinder before it comes to rest is:
n=Rω208πμg
The cylinder experiences gravitational force mg downward, normal forces n1 (from the floor) and n2 (from the wall), and frictional forces f1 (from the floor) and f2 (from the wall).
1. Vertical Forces: The sum of vertical forces must equal zero.
n1+f2−mg=0(1)
Rearranging gives:
n1+f2=mg
f1−n2=0(2)
This implies:
f1=n2
Using the coefficient of friction μ:
- The frictional force from the floor:
f1=μn1
- The frictional force from the wall:
f2=μn2
Substituting f2 into equation (1):
n1+μn2=mg
Substituting n2 from equation (2):
n1+μf1=mg
Since f1=μn1:
n1+μ2n1=mg
Factoring out n1:
n1(1+μ2)=mg
Thus,
n1=mg1+μ2
Now substituting n1 back to find n2:
n2=μn1=μmg1+μ2
The work done by the friction forces is equal to the change in kinetic energy:
Work=−f1Rθ−f2Rθ=−Rθ(f1+f2)
Substituting f1 and f2:
=−Rθ(μn1+μn2)=−Rθ(μmg1+μ2+μ2mg1+μ2)
This simplifies to:
=−Rθ⋅μmg(1+μ2)1+μ2=−μmgRθ
The initial kinetic energy of the cylinder is:
KEi=12Iω20=12⋅12mR2ω20=mR2ω204
The final kinetic energy is zero when the cylinder comes to rest:
Work=ΔKE=KEf−KEi=0−mR2ω204
Setting the work done equal to the change in kinetic energy:
−μmgRθ=−mR2ω204
Canceling m and rearranging gives:
θ=Rω204μg
Since θ is in radians, the number of revolutions n is given by:
n=θ2π=Rω204μg⋅2π=Rω208πμg
The number of revolutions made by the cylinder before it comes to rest is:
n=Rω208πμg
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT TEXTBOOK EXERCISES )21videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )12videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions24videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A cylinder is rotating with angular velocity ω0 and is gently put on a rough horizontal floor. Assume mass of the cylinder is m and radius R. Calculate the velocity of cylinder when it starts pure rolling on the surface.
View SolutionThe motor of an engine is rotating about its axis with angular velocity of 120r±. It comes to rest in 10s, after being switched off. Assuming constant deceleration, calculate the number of revolutions made by it before coming to rest.
View Solution
Knowledge Check
- Question 1 - Select One
Consider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P? It is assumed that the cylinder does not slip.
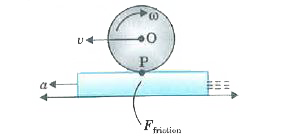 AMgBMaCMa2DMa3
AMgBMaCMa2DMa3 - Question 2 - Select One
A hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
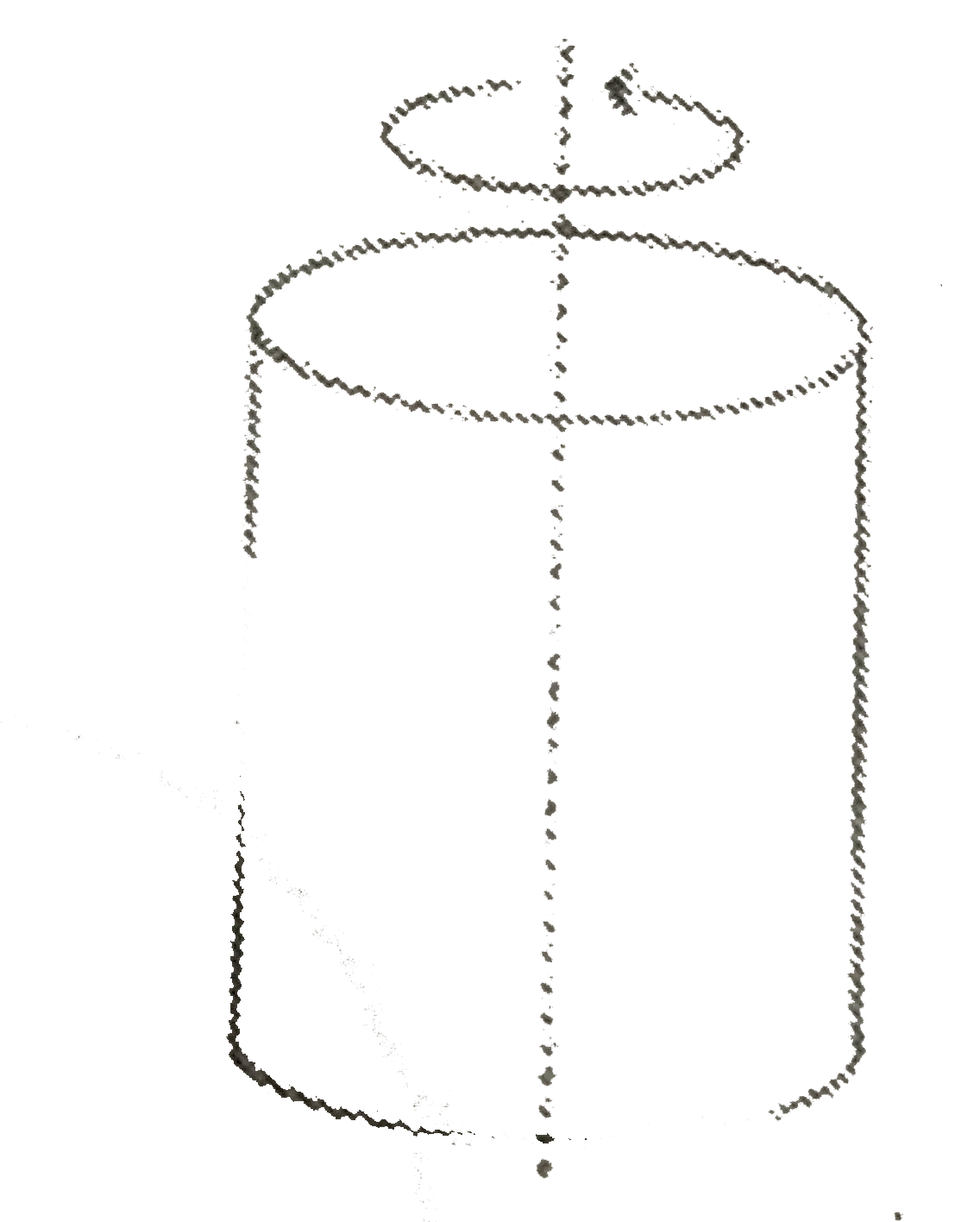 Aμ=gRω2Bμ=ω2gRCμ=ω2RgDμ=gω2R
Aμ=gRω2Bμ=ω2gRCμ=ω2RgDμ=gω2R - Question 3 - Select One

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3m
A spinning cylinder with angular velocity ω0 of mass M and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1/√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
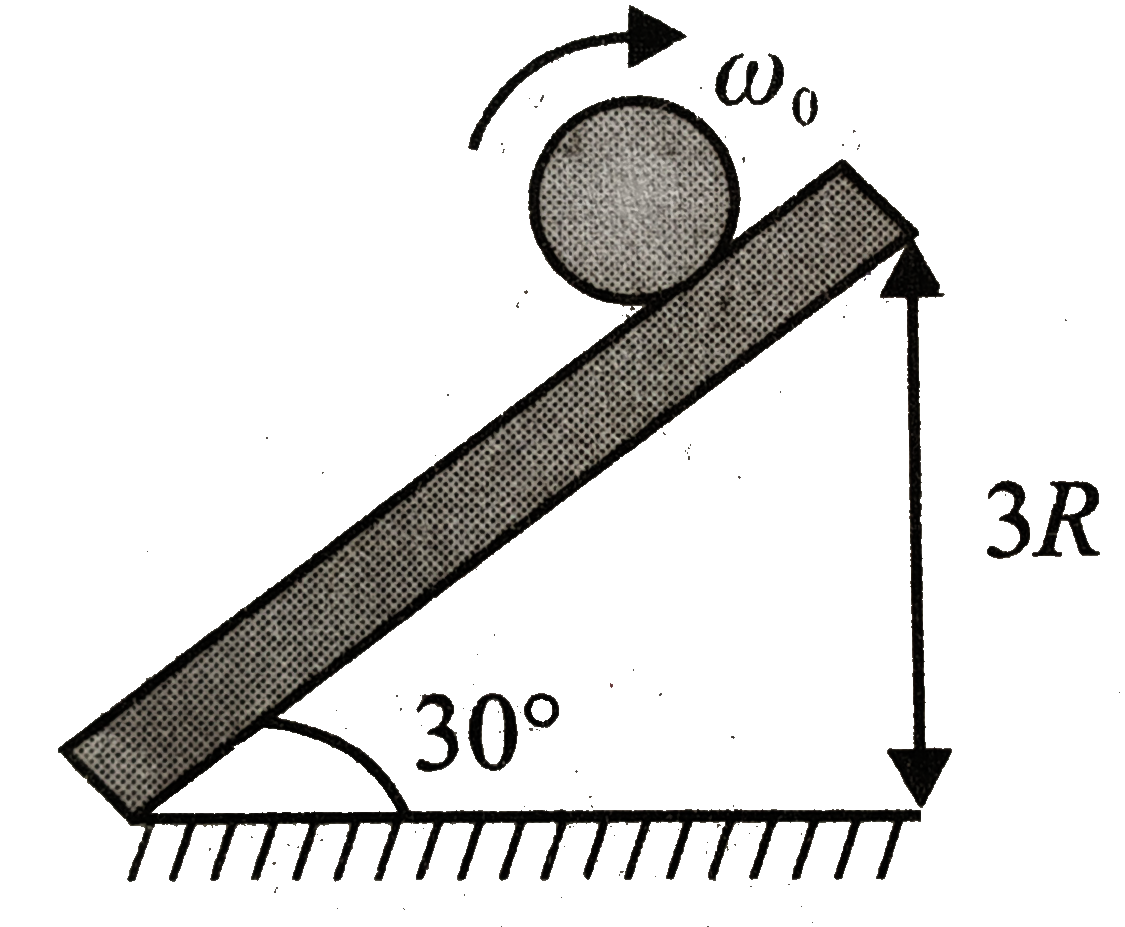 View Solution
View SolutionThe motor of an engine is rotating about its axis with an angular velocity of 100rpm. It comes to rest in 15s, after being switched off. If angular deceleration is constant, what is the number to revolutions made by it before coming to rest ?
View SolutionA uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?
 View Solution
View SolutionConsider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P ? It is assumed that the cylinder does not slip.
 View Solution
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View Solution

