A cylindrical object of outer diameter 20 cm height 20 cm and density 8000 is supported by a vertical spring and is half dipped in water as shown in figue. a. Figure the elongation of the spring in equilibrium condition. b. If the object is sllightlly depressed and relation, find the time period of resulting oscillations of the objcet. The spring constant .

The correct Answer is:A, B, C
a. Here
rarr 500xx10^3xx(x)=pir^2xxhxx1000(rho-1/2)=pixx(5)^2xx20xx1000(rho_b-1/2)rarr 50x=pixx25xx2xx(rho_b-1/2)=x=pi(8-0.5)x=pixx7.5=23.5cmF=kX+Vrho_wxxgrarr ma=kX+pir^2xx(X)xxrho_wxxg=(k+pir^2xxrho_wxxg)Xrarr omega^2xx(X)=((k+pir^2+rho_wxxg))/m xx(X)[because a=w^2XinSHM]rarr T=2i m/(k+pir^2+rho_wxxg) =2pi(pixx25xx20xx8)/(500+10^3+pix25xx1xx1000)=0.935s.
Topper's Solved these Questions
Similar Questions
A cylindrical object of outer diameter 20 cm and mass 2 kg flots in wter with its axis vertical. If it si lightly depressed and then released, find the time peiod of the resulting simple harmonic motion of the object.
View SolutionA rectangular tank having base 15cm×20cm is filled with water (density ρ=1000kg/m2) up to 20cm and force constant K=280N/m is fixed to the bottom of the tank so that the spring remains vertical.
This system is in an elevator moving downwards with acceleration a=2m/s2. A cubical block of side l=10cm and mass m=2kg is gently placed over the spring and released gradually, as shown in the figure.

a. Calculate compression of the spring in equilibrium position.
b. If the block is slightly pushed down from equilibrium position and released, calculate frequency of its vertical oscillations.
View Solution
Knowledge Check
A 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. The time period of oscillation is
Aπ5sBπ2sCπsD2πs
A wooden block of mass 0.5 kg and density 800 kgm−3 is fastened to the free end of a vetical spring of spring cosntant 50 Nm−1 fixed at the bottom. If the entire system is completely immersed in water, find a. the elongation (or compresion) of the spring in equilibrium and b. the time period of vertical oscillations of het block when it is slightly depressed and released.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

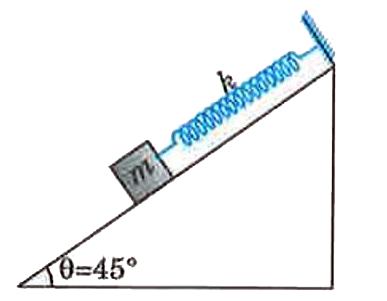
View SolutionA spring of unstretched length 40 cm and spring constant k is attached to a block of mass 1 kg to one of its end. The other end of the spring is fixed on the top of a frictionless inclined plane of inclination θ=45∘ as shown in the figure, so that the spring extends by 3 cm. When the mass is displaced slightly and released the time period of the resulting oscillation is T. Determine the value of 5T close to nearest integer.
View SolutionA copper piece of mas 10 g is suspended by a vertical spring. The sprig elongates 1 cm over its natural lenngth to keep the piece in equilibrium. A beaker containing water is now placed below the piece so as to immerse the piece completely in water. Find the elongation of the spring. Density of copper =9000 kgm^-3. Takeg=10ms−2
View Solution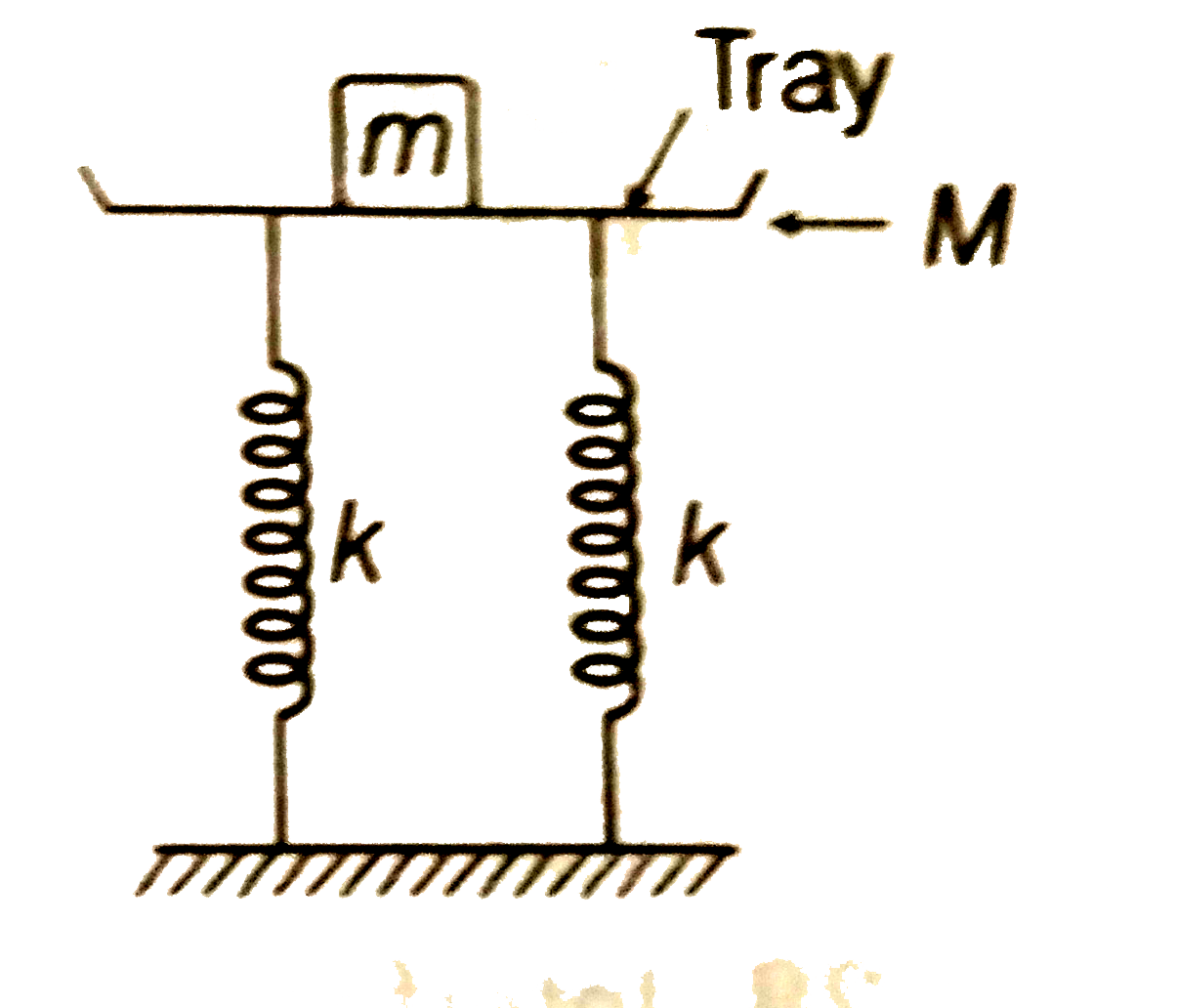
A tray of mass M=10kg is supported on two identical springs, each of spring constant k, as shown in figure, when the tray is depressed a little and released, it executes simple harmonic motion of period 1.5 s. when a blockof mass m is placed on the tray, the speed of oscillation becomes 3 s. the value of m is
View SolutionOne end of a massless spring of relaxed length 50cm and spring constant k is fixed on top of a frictionless inclined plane of inclination theta=30degree as shown in fig. When a mass m=1.5kg is attached at the other end, the spring extends by 2.5cm when the block in equilibrium .The mass is displaced slightly from equilibrium position and released. The time period (in seconds) of the resulting oscillation will be (g=9.8m/s^(2))
View SolutionA metal piece of mass 10g is suspended by a vertical spring. The spring elongates 10cm over its natural length to keep the piece in equilibrium. A beaker containing water is now placed below the piece so as to immerse the piece completely in water. Find the elongation of the spring. Density of metal =9000kg/m3. Take g=10m/s2.
View Solution
