Question

(a) Define the term 'conductivity' of a metallic wire. Write its SI unit.
(b) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in te'rms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.

Explanation

(a) The resistivity and conductivity are proportionally constant and, therefore, depend only on the material the wire is made of not the geometry of wire.
The reciprocal of resistivity of the material of a conductor is called conductivity.
S.I unit = mho - `m^(-1)`/ siemen `m^(-1)`.
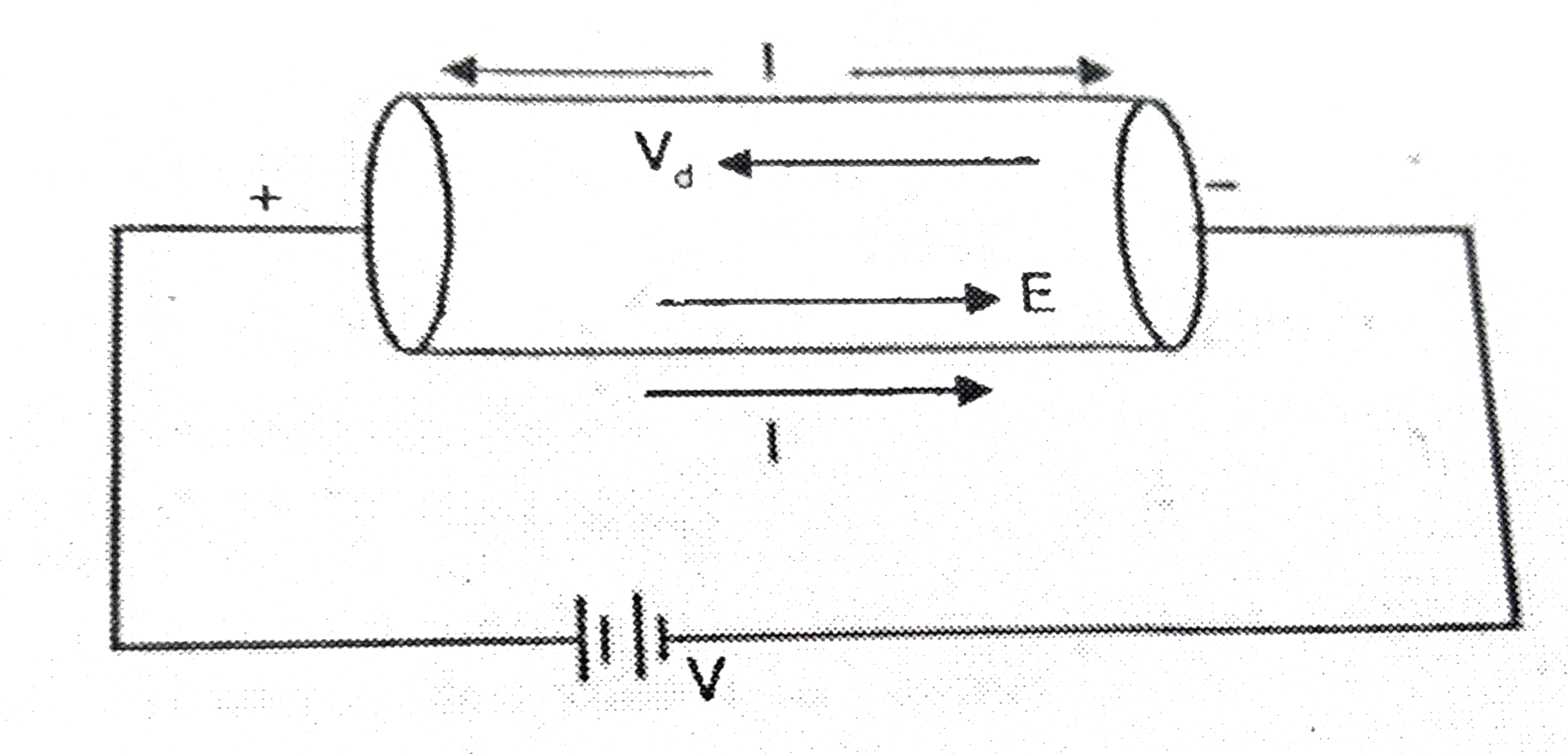
(b) Let us consider a wire of length l and cross-sectional area A. When potential V is applied at the terminals of wire then electric field F. generate inside the conductor and all the `e^(-1)` flow towards the+ ve terminal of bett'ery with drift velocity Vd.
Let the conductor no. of `e^(-1)` per units.
Volue is n then no. of `e^(-)` in it .
= Volume of wire `xx e^(-1)` density = area `xx` lenght Xn = Aln.
If charge of each electron ,is e, then total frequency charge q = nAle
If the time taken by the electrons to cover the distance l is =
`Detla = l//Vd`
Floing current `i = (q) /(Deltat)`
`i = (n Ale)/(l//Vd) = nAeVd`
We know that current density
`J = (i)/(A) = (cancel(nAe)V_(d))/(cancel(A))`
`J = "ne"Vd`
Drift volocity `V_(d) = ((eEtau)/(m))`
Where, `tau =` Relaxtion time
Then, `J = ne ((eEtau)/(m))`
`J = (ne^(2) tauF)/(m)`
`J = sigma E` where `sigma = ("ne"^(2)tau)/(m)`.