A flat circular coil of n turns, area A and resitance R is placed in a uniform magnetic field B. The pane of coil is initially perpedicular of B. when the coil is rotated through an angle of 180∘ about one of its diameter, a charge Q1 flows through the coil When the same coil after charge Q2 flows through it. then Q2/Q1 is
(a) 1
(b) 2
(c) 1/2
(d) 0
The correct Answer is:D
To solve the problem, we will use the principles of electromagnetic induction and the formula for induced electromotive force (emf). The charge flowing through the coil can be calculated using the relationship between charge, current, and time.
1. Understanding the Initial Conditions:
- The coil has n turns, area A, and resistance R.
- It is placed in a uniform magnetic field B, initially perpendicular to the plane of the coil.
2. Induced EMF Calculation:
- The magnetic flux (Φ) through the coil is given by:
\(
\Phi = B \cdot A \cdot \cos(\theta)
\)
- Initially, when the coil is perpendicular to the magnetic field, \(\theta = 0^\circ\) and \(\cos(0) = 1\):
\(
\Phi_1 = B \cdot A
\)
3. Rotation of the Coil:
- When the coil is rotated through an angle of \(180^\circ\), the new angle \(\theta = 180^\circ\) and \(\cos(180) = -1\):
\(
\Phi_2 = B \cdot A \cdot \cos(180^\circ) = -B \cdot A
\)
4. Change in Magnetic Flux:
- The change in magnetic flux (ΔΦ) is given by:
\(
\Delta \Phi = \Phi_2 - \Phi_1 = -B \cdot A - (B \cdot A) = -2B \cdot A
\)
5. Induced EMF (ε):
- According to Faraday's law of electromagnetic induction, the induced emf (ε) is given by:
\(
\varepsilon = -n \frac{\Delta \Phi}{\Delta t}
\)
- Assuming the rotation takes a time Δt, we have:
\(
\varepsilon = -n \frac{-2B \cdot A}{\Delta t} = \frac{2nBA}{\Delta t}
\)
6. Current Calculation:
- The induced current (I) in the coil can be calculated using Ohm's law:
\(
I = \frac{\varepsilon}{R} = \frac{2nBA}{R \Delta t}
\)
7. Charge Calculation:
- The charge (Q) that flows through the coil during the time Δt is given by:
\(
Q = I \cdot \Delta t = \left(\frac{2nBA}{R \Delta t}\right) \cdot \Delta t = \frac{2nBA}{R}
\)
- Thus, the charge \(Q_1\) when the coil is rotated through \(180^\circ\) is:
\(
Q_1 = \frac{2nBA}{R}
\)
8. Returning to the Original Position:
- If the coil is rotated back to its original position (0 degrees), the same change in flux occurs, and thus the charge \(Q_2\) will also be:
\(
Q_2 = \frac{2nBA}{R}
\)
9. Finding the Ratio \(Q_2/Q_1\):
- Since both \(Q_1\) and \(Q_2\) are equal:
\(
\frac{Q_2}{Q_1} = \frac{\frac{2nBA}{R}}{\frac{2nBA}{R}} = 1
\)
Final Answer:
\(
\frac{Q_2}{Q_1} = 1
\)
- The coil has n turns, area A, and resistance R.
- It is placed in a uniform magnetic field B, initially perpendicular to the plane of the coil.
- The magnetic flux (Φ) through the coil is given by:
\(
\Phi = B \cdot A \cdot \cos(\theta)
\)
- Initially, when the coil is perpendicular to the magnetic field, \(\theta = 0^\circ\) and \(\cos(0) = 1\):
\(
\Phi_1 = B \cdot A
\)
- When the coil is rotated through an angle of \(180^\circ\), the new angle \(\theta = 180^\circ\) and \(\cos(180) = -1\):
\(
\Phi_2 = B \cdot A \cdot \cos(180^\circ) = -B \cdot A
\)
- The change in magnetic flux (ΔΦ) is given by:
\(
\Delta \Phi = \Phi_2 - \Phi_1 = -B \cdot A - (B \cdot A) = -2B \cdot A
\)
- According to Faraday's law of electromagnetic induction, the induced emf (ε) is given by:
\(
\varepsilon = -n \frac{\Delta \Phi}{\Delta t}
\)
- Assuming the rotation takes a time Δt, we have:
\(
\varepsilon = -n \frac{-2B \cdot A}{\Delta t} = \frac{2nBA}{\Delta t}
\)
- The induced current (I) in the coil can be calculated using Ohm's law:
\(
I = \frac{\varepsilon}{R} = \frac{2nBA}{R \Delta t}
\)
- The charge (Q) that flows through the coil during the time Δt is given by:
\(
Q = I \cdot \Delta t = \left(\frac{2nBA}{R \Delta t}\right) \cdot \Delta t = \frac{2nBA}{R}
\)
- Thus, the charge \(Q_1\) when the coil is rotated through \(180^\circ\) is:
\(
Q_1 = \frac{2nBA}{R}
\)
- If the coil is rotated back to its original position (0 degrees), the same change in flux occurs, and thus the charge \(Q_2\) will also be:
\(
Q_2 = \frac{2nBA}{R}
\)
- Since both \(Q_1\) and \(Q_2\) are equal:
\(
\frac{Q_2}{Q_1} = \frac{\frac{2nBA}{R}}{\frac{2nBA}{R}} = 1
\)
\(
\frac{Q_2}{Q_1} = 1
\)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions3videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective21videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Assertion And Reason10videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A flat coil, C, of n turns, area A and resistance R, is placed in a uniform magnetic field of magnitude B. The plane of the coil is initially perpendicular to B. The coil,is rotated by an angle θ about a diameter and charge of amount Q flows through it. Choose the correct alternatives.
View SolutionIn the above problem. The plane of the coil is initially kept parallel to B. The coil is rotated by an angle θ about the diameter perpendicular to B and charge of amount Q flows through it. Choose the correct alternatives.
View SolutionIf number of turns of 70cm2 coil is 200 and it is placed in a magnetic field of 0.8Wb/m2 which is perpendicular to the plane of coil and it is rotated through an angle 180∘ in 0.1 sec , then induced emf in coil :
View SolutionCurrent I is flowing through a circular coil of radius r. It is placed in a magnetic field B in such a way that the plane of the circular coil is perpendicular to B. The force acting on it will be -
View SolutionA current I flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
View SolutionA flip coil consits of N turns of circular coils which lie in a uniform magnetic field. Plane of the coils is perpendicular to the magnetic field as shown in figure. The coil is connected to a current integrator which measures the total charge passing through it. The coil is turned through 180∘ about the diameter. The charge passing through the coil is
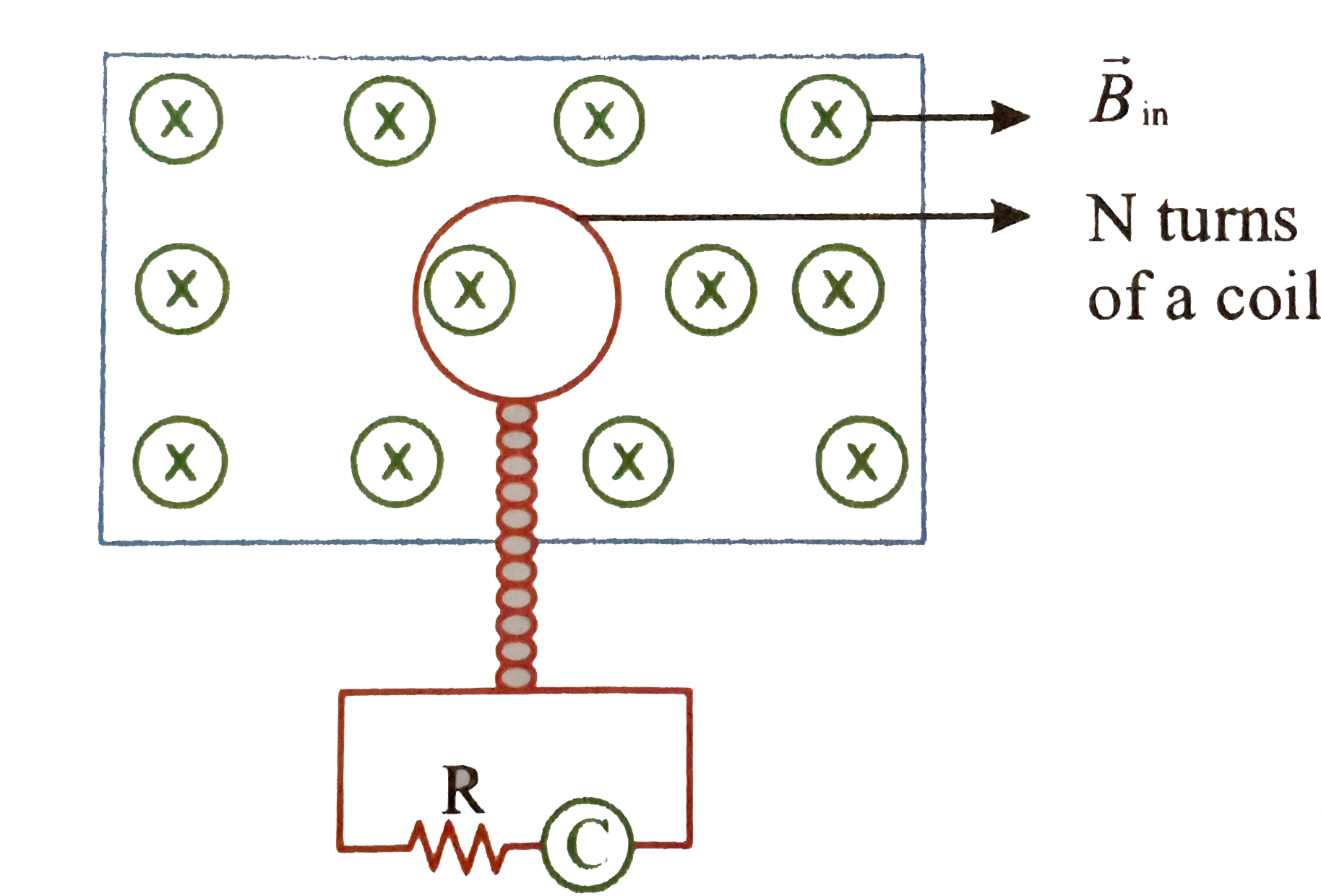 View Solution
View SolutionA wire of length l is bent in the form a circular coil of some turns. A current I flows through the coil. The coil is placed in a uniform magnetic field B. The maximum torqur on the coil can be
View SolutionA rectangular coil of area A, having number of turns N is rotated at 'f' revoluation per second in a uniform magnetic field B, the field being perpendicular to the coil. Prove that maximum emf induced in the coil is 2πfNBA.
View SolutionA coil of cross-sectional area A having n turns is placed in uniform magnetic field B. When it is rotated with an angular velocity ω, the maximum e.m.f. induced in the coil will be :
View SolutionA rectangular copper coil is placed in a uniform magnetic field of induction 40 mT with its plane perpendicular to the field. The area of the coil is shrinking at a constant rate of 0.5m2s−1. The emf induced in the coil is
View Solution

