A force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
positive in displacing the block from x = 3 to x = 1
positive in displacing the block from x = - 1 to x = - 3
negative in displacing the block from x = 3 to x = 1
negative in displacing the block from x = - 1 to x = - 3
The correct Answer is:A, D
To find the work done by the force F=−kx3 acting on a block moving along the x-axis, we can follow these steps:
Step 1: Understand the Work Done
The work done W by a force when an object moves from position xi to position xf is given by the integral of the force over the displacement:
W=∫xfxiFdx
Step 2: Substitute the Force
We substitute the expression for the force F=−kx3 into the work done formula:
W=∫xfxi−kx3dx
Step 3: Integrate the Force
Now we perform the integration:
W=−k∫xfxix3dx
The integral of x3 is:
∫x3dx=x44
Thus, we can write:
W=−k(x44)xfxi
Step 4: Evaluate the Integral
Now we evaluate the definite integral:
W=−k⎛⎝x4f4−x4i4⎞⎠
This simplifies to:
W=−k4(x4f−x4i)
Step 5: Final Expression for Work Done
Thus, the work done by the force F=−kx3 when moving from xi to xf is:
W=−k4(x4f−x4i)
The work done W by a force when an object moves from position xi to position xf is given by the integral of the force over the displacement:
W=∫xfxiFdx
We substitute the expression for the force F=−kx3 into the work done formula:
W=∫xfxi−kx3dx
Now we perform the integration:
W=−k∫xfxix3dx
The integral of x3 is:
∫x3dx=x44
Thus, we can write:
W=−k(x44)xfxi
Now we evaluate the definite integral:
W=−k⎛⎝x4f4−x4i4⎞⎠
This simplifies to:
W=−k4(x4f−x4i)
Thus, the work done by the force F=−kx3 when moving from xi to xf is:
W=−k4(x4f−x4i)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions18videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - D Matrix Matching Type Questions10videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct42videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
The force acting on a particle moving along X-axis is F=−k(x−v0t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks the particle . What kind of motion does he find for the particle?
View SolutionThe variation of force F acting on a body moving along x - axis varies with its position (x) as shown in figure
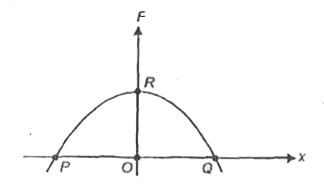
The body is in stable equilibrium stable atView SolutionThe force acting on a body moving along x -axis varies with the position of the particle as shown in the fig. The body is in stable equilibrium at.
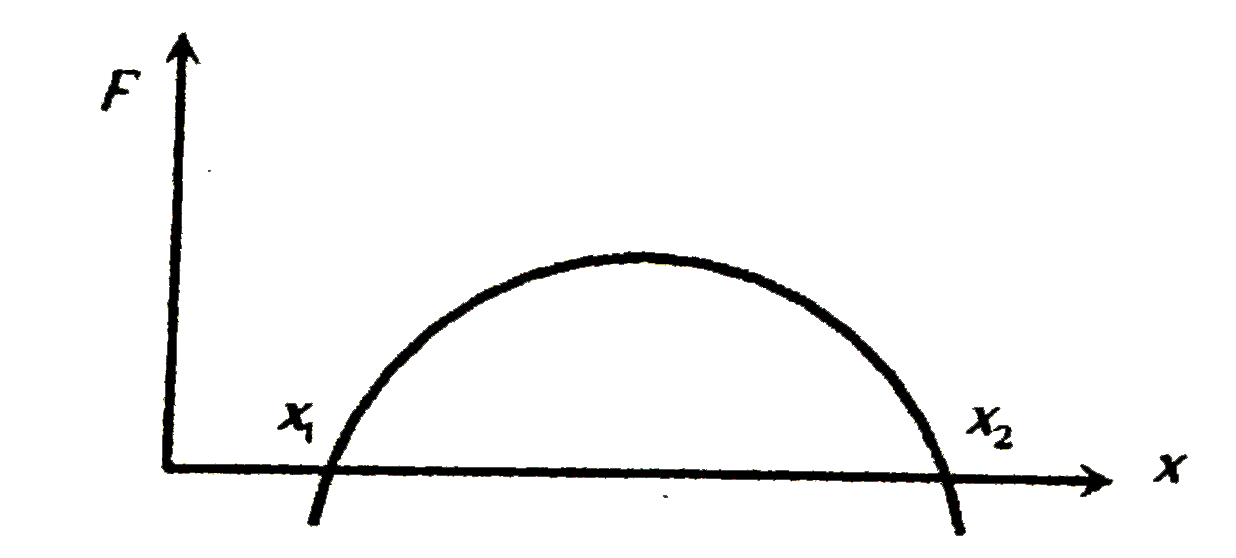View SolutionA force F=a+bx acts on a particle in the x-directioin, where a and b are constants. Find the work done by this force during a displacement form x=0→x=d.
View SolutionA force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View SolutionA particle of mass m moves with a variable velocity v, which changes with distance covered x along a straight line as v=k√x, where k is a positive constant. The work done by all the forces acting on the particle, during the first t seconds is
View SolutionA force f=10+2x acts on a particle moving in straight line on x axis the work done by this force during a displacement from x=0 and x=3m
View SolutionThe force acting on a body moving along x-axis variation of the particle particle shown in the figure. The body is in stable equilibrium at
. View SolutionA particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
View SolutionA force F acting on an object varies with distance x as shown here.
The force is in N and x in m. The work done by the force in moving the object from x = 0 to x = 6 m isView Solution