A force of 20N is applied on a body of mass 5 kg resting on a horizontal plane. The body gains a kinetic energy of 10 after is moves a distance 2m. The fricitional force is
10N
15N
20N
30N
The correct Answer is:B
To solve the problem, we need to find the frictional force acting on a body when a force is applied to it. Here’s a step-by-step solution:
Step 1: Identify the given data
- Applied force (F) = 20 N
- Mass of the body (m) = 5 kg
- Kinetic energy gained (KE) = 10 J
- Distance moved (s) = 2 m
Step 2: Use the kinetic energy formula to find the velocity
The formula for kinetic energy is given by:
KE=12mv2
Substituting the known values:
10=12×5×v2
This simplifies to:
10=52v2
Multiplying both sides by 2:
20=5v2
Now, dividing both sides by 5:
v2=4
Taking the square root:
v=2 m/s
Step 3: Calculate the acceleration using the kinematic equation
We can use the equation of motion:
v2=u2+2as
Where:
- v = final velocity = 2 m/s
- u = initial velocity = 0 m/s (since the body is at rest)
- s = distance = 2 m
Substituting the values:
4=0+2a×2
This simplifies to:
4=4a
Dividing both sides by 4:
a=1 m/s2
Step 4: Apply Newton's second law to find the frictional force
According to Newton's second law, the net force acting on the body is given by:
Fnet=m⋅a
Where:
- Fnet=F−Ff (where Ff is the frictional force)
Substituting the known values:
Fnet=5⋅1=5 N
Now, we know that:
Fnet=F−Ff
Substituting the values:
5=20−Ff
Rearranging gives:
Ff=20−5=15 N
Final Answer
The frictional force acting on the body is 15 N.
---
- Applied force (F) = 20 N
- Mass of the body (m) = 5 kg
- Kinetic energy gained (KE) = 10 J
- Distance moved (s) = 2 m
The formula for kinetic energy is given by:
We can use the equation of motion:
- v = final velocity = 2 m/s
- u = initial velocity = 0 m/s (since the body is at rest)
- s = distance = 2 m
According to Newton's second law, the net force acting on the body is given by:
- Fnet=F−Ff (where Ff is the frictional force)
The frictional force acting on the body is 15 N.
Topper's Solved these Questions
Similar Questions
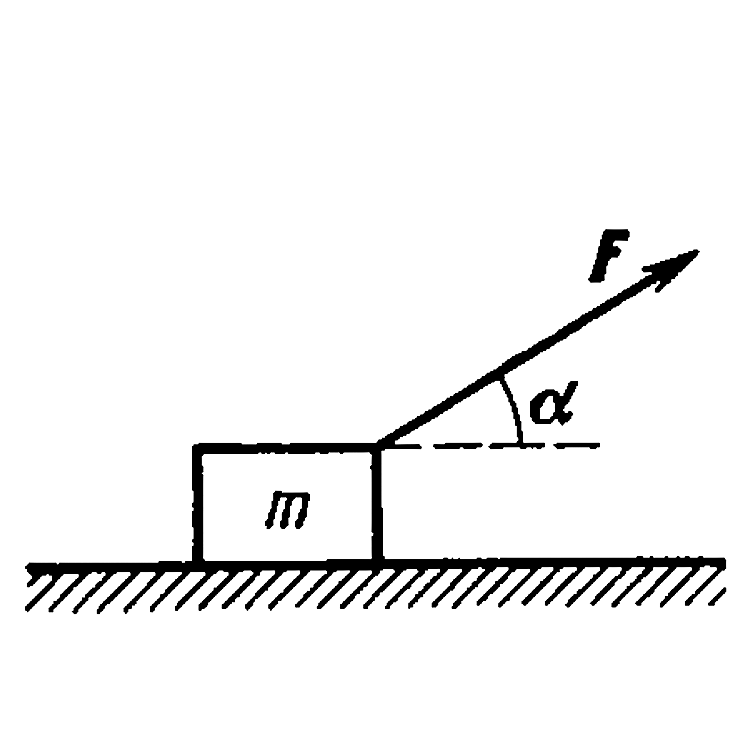
At the moment t=0 the force F=at is applied to a small body of mass m resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle α with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
View SolutionA force acts for 8 s on a body of mass 5 kg at rest,on a smooth horizontal surface.The force then stops acting and the body describes 80 m in next 5 s .The force acting on body is
View Solution
Knowledge Check
A constant force of 20N is applied to pull a body of mass 10 k, kept on a smooth horizontal surface. What is the increase in its kinetic energy if the body starts from rest and covers a distance of 5m?
A100JB150JC80JD60JA constant force of 5 N is applied on a block of mass 20 kg for a distance 2 0 m. The kinetic energy acquired by the block is
A20 JB15 JC10 JD5 JA body moving with a kinetic energy of 6J cmes to rest at a distance of 1m due to a retarding force of
A4NB6NC5ND8N
A force acts for 8 s on a body of mass 5kg at rest,on a smooth horizontal surface.The force then stops acting and the body describes 80m in next 5s .The force acting on body is ?
View SolutionA uniform force of 4 N acts on a body of mass 40 kg for a distance of 2 m. The kinetic energy acquired by the body is
View SolutionA uniform force of 4 N acts on a body of mass 40 kg for a distance of 2 m. The kinetic energy acquired by the body is
View SolutionIf a body has kinetic energy. T, moving on a rough horizontal surface stops at distance y. The frictional force exerted on the body is
View SolutionAt t=0, a force F=at2 is applied to s small body of mass m at an angle α resting on a smooth horizontal plane.
View Solution
