A gardener presses the grasscutter with a force at an angle . Assume the motion of grasscutter as pure rolling. Find the:
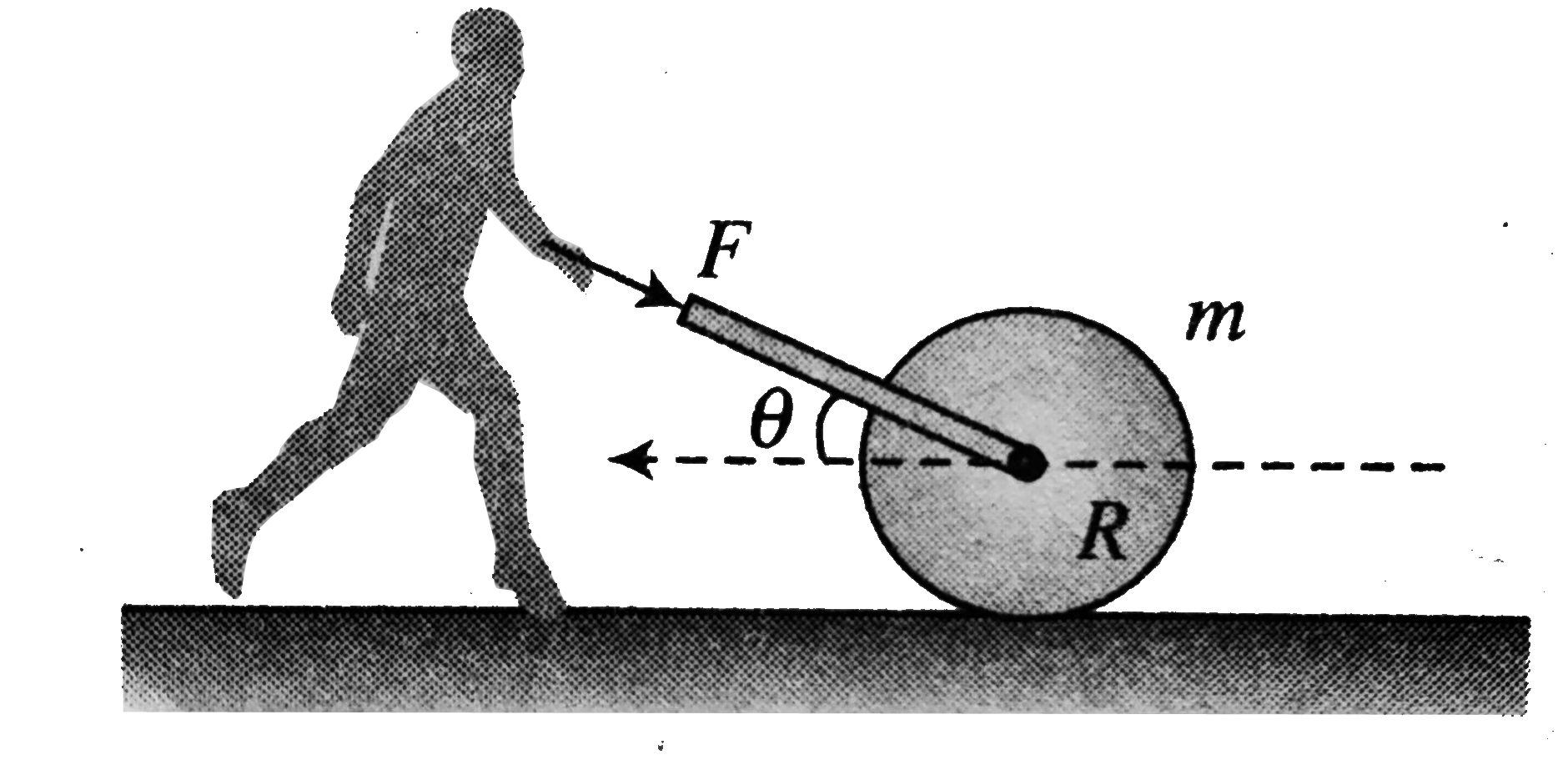
Acceleration of of the roller (disc). Assume that the mass of the disc is and neglect the mass of the connecting rod.
The correct Answer is:A
…………i
………ii
From i and ii
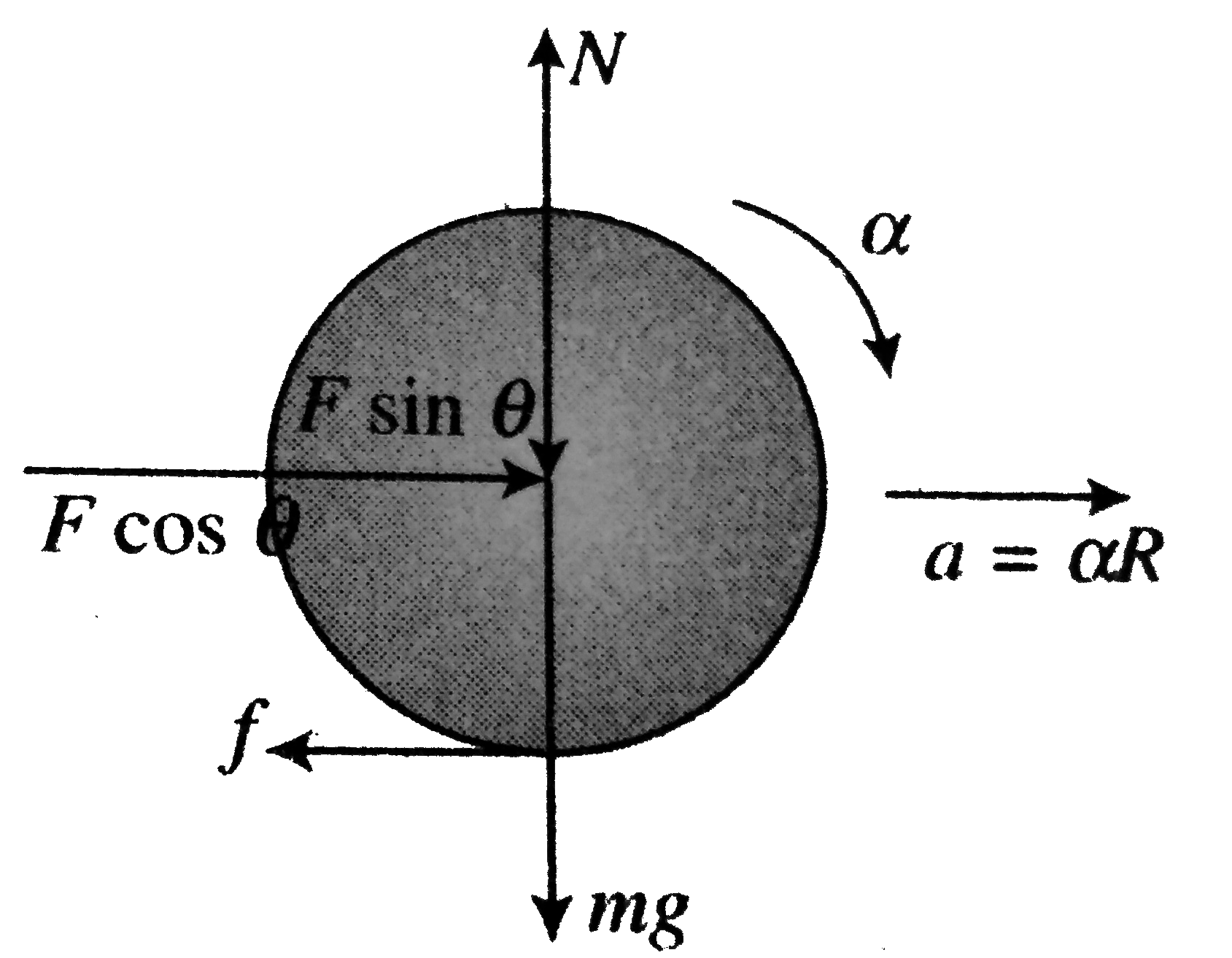
Now
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A gardener presses the grasscutter with a force F at an angle θ. Assume the motion of grasscutter as pure rolling. Find the:

friction between the grasscutter (assumed as a disc) and ground.View SolutionA gardener presses the grasscutter with a force F at an angle θ. Assume the motion of grasscutter as pure rolling. Find the:
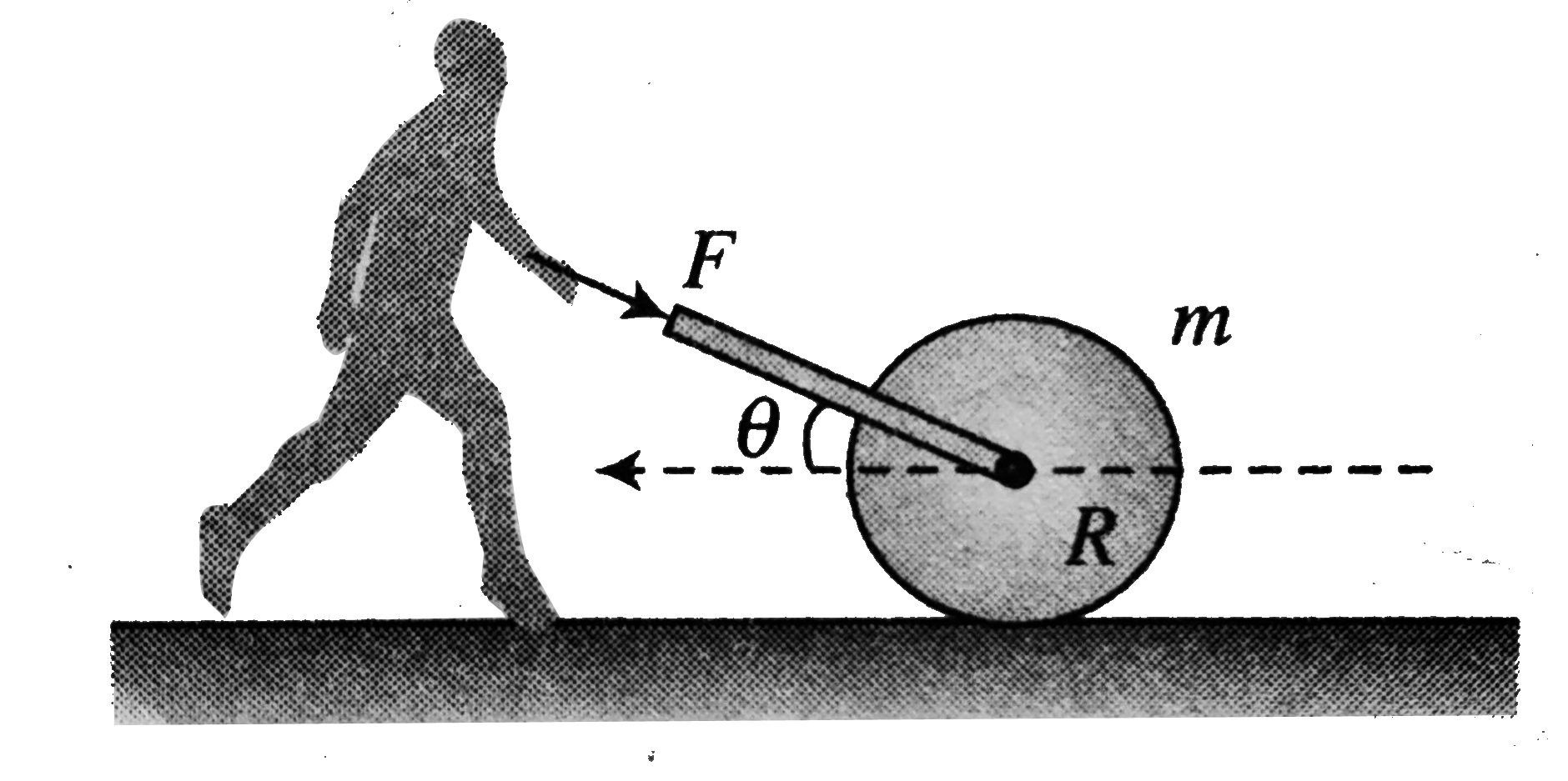
Maximum force F for no relative slidng if th coeficient of friction between the roller and ground is μView Solution
Knowledge Check
- Question 1 - Select One

A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.Aa. Acceleration of disc = 2F/3mBb. Friction force between disc and surface = 2F/3Cc. Acceleration of disc = 6F/5mDd. Friction force between disc and surface is F/3
A spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown Fig. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass m is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is M and radius is R. Find the acceleration of the falling mass m. Neglect the mass of the connecting tube and slipping of the spool.
 View Solution
View Solution
A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.View SolutionA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:
 View Solution
View SolutionA force F is applied onn a spool (mass m and radius R) in vertical direction as shown in case I and case II. The radius of gyration k of spool is R/(√2). Assuming pure rolling, find the acceleration of the CM of the body, assuming it as a uniform cylinder of mass m.
 View Solution
View SolutionThe acceleration of the centre of mass of uniform solid disc rolling down an inclined plane of angle α is xgsinα. Find x
View SolutionA uniform disc of mass m and radius R is projected horizontally with velocity v0 on a rough horizontal floor so that it starts off with a purely sliding motion at t=0. After t0 seconds, it acquires pure rolling motion as shown in the figure.
(a) Calculate the velocity of the center of mass of the disc at t0.
Assuming that the coefficent of friction to be μ, calculate t0.
 View Solution
View SolutionShown in the diagram is a system of two bodies, a block of mas m and a disc of mass M, held in equilibrium. If the string 3 is burnt, find the acceleration of the disc. Neglect the masses of the pulleys P and Q. (The coefficient of friction between the block and horizontal surface is μ)
 View Solution
View Solution

