A hemispherical bowl of radius R si set rotating abouv its axis of symmetry whichis kept vertical. A small blcok kept in the bowl rotates with the bowl without slippingn on its surface. If the surfaces of the bowl is mooth, and the abgel made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
To solve the problem of finding the angular speed at which a hemispherical bowl of radius R rotates when a small block is placed inside it at an angle θ with the vertical, we can follow these steps:
Step 1: Understand the Setup
We have a hemispherical bowl with radius R rotating about its vertical axis. A small block is placed inside the bowl and makes an angle θ with the vertical. The radius of the circular path traced by the block is r=Rsinθ.
Step 2: Identify Forces Acting on the Block
The forces acting on the block are:
- The gravitational force mg acting downwards.
- The normal reaction force N acting perpendicular to the surface of the bowl.
Step 3: Draw the Free Body Diagram (FBD)
In the FBD, the normal force N can be resolved into two components:
- Ncosθ acting vertically upward.
- Nsinθ acting horizontally towards the center of the bowl (providing the centripetal force).
Step 4: Set Up the Equations
1. Vertical Force Balance: The vertical component of the normal force balances the weight of the block:
Ncosθ=mg(1)
2. Horizontal Force (Centripetal Force): The horizontal component of the normal force provides the required centripetal force for circular motion:
Nsinθ=mω2r(2)
where r=Rsinθ.
Step 5: Substitute r in Equation (2)
Substituting r into equation (2):
Nsinθ=mω2(Rsinθ)(3)
Step 6: Divide Equation (3) by Equation (1)
Dividing equation (3) by equation (1) to eliminate N:
NsinθNcosθ=mω2(Rsinθ)mg
This simplifies to:
tanθ=ω2Rsinθg
Step 7: Rearrange to Solve for ω2
Rearranging gives:
ω2=gtanθRsinθ
Using the identity tanθ=sinθcosθ, we can rewrite it as:
ω2=gsinθRsinθcosθ
This simplifies to:
ω2=gRcosθ
Step 8: Take the Square Root
Finally, taking the square root gives us the angular speed:
ω=√gRcosθ
Final Result
The angular speed at which the bowl is rotating is:
ω=√gRcosθ(radians per second)
---
We have a hemispherical bowl with radius R rotating about its vertical axis. A small block is placed inside the bowl and makes an angle θ with the vertical. The radius of the circular path traced by the block is r=Rsinθ.
The forces acting on the block are:
- The gravitational force mg acting downwards.
- The normal reaction force N acting perpendicular to the surface of the bowl.
In the FBD, the normal force N can be resolved into two components:
- Ncosθ acting vertically upward.
- Nsinθ acting horizontally towards the center of the bowl (providing the centripetal force).
1. Vertical Force Balance: The vertical component of the normal force balances the weight of the block:
Ncosθ=mg(1)
Nsinθ=mω2r(2)
where r=Rsinθ.
Substituting r into equation (2):
Nsinθ=mω2(Rsinθ)(3)
Dividing equation (3) by equation (1) to eliminate N:
NsinθNcosθ=mω2(Rsinθ)mg
This simplifies to:
tanθ=ω2Rsinθg
Rearranging gives:
ω2=gtanθRsinθ
Using the identity tanθ=sinθcosθ, we can rewrite it as:
ω2=gsinθRsinθcosθ
This simplifies to:
ω2=gRcosθ
Finally, taking the square root gives us the angular speed:
ω=√gRcosθ
The angular speed at which the bowl is rotating is:
ω=√gRcosθ(radians per second)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -1
16 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -2
6 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
Similar Questions
A hemispherical bowl of radius R si set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View SolutionA hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical.A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.
View SolutionA hemispherical bowl of radius R is rotating about its own axis (which is vertical) with an angular velocity ω . A particle on the frictionless inner surface of the bowl is also rotating with the same ω . The particle is a height h from the bottom of the bowl.
(i) Obtain the relation between h and ω _________
(ii) Find minimum value of ω needed, in order to have a non-zero value of h _____________ .
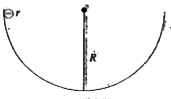
View SolutionA spherical bowl of radius R rotates about the verical diameter with angular velocity ω.The bowl contains a small object inside and in absence of friction, this object takes up a position inside the bowl such that its radius vector makes an angle θ with the vertical (see figure). Then

View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
View SolutionA hemispherical bowl of radius R carries a uniform surface charge density σ. Find the potential at the topmost point A, taking potential at infinity to be zero.
View SolutionThe radius of a large hemisphere whose" axis of symmetry is vertical is R = 50 cm. A small sphere of radius r= 5cm rolls without slipping with a speed of 2cm/s. The mass of the sphere is 100 gm. If it start's at the top from rest (i) what is the kinetic energy at the bottom? (ii) What fraction is rotational ? (iii) What fraction is translational?
View Solution
A small mass of 10 g lies in a hemispherical bowl of radius 0.5 m at a height of 0.1 m from the bottom of the bowl. The mass will be in equilibrius if the bowl rotates at an
View Solution
