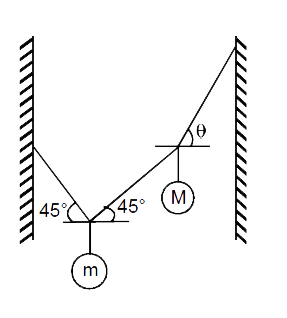
A large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and θ is the 'angle' this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?

The correct Answer is:1
The mass m is acted by two forces
(i) Weight mg a mass M (ii) Tension T in the string
Tcosθ=mg,Tsinθ=mrω2 and T = Mg
r=lsinθ,Mgsinθ=m(lsinθ)ω2
ω2=Mgml,n=12π√Mgml
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Matrix - Match
Explore 5 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Comprehension type Queston
Explore 14 Videos
Similar Questions
A large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular peth which lies in a horizantal plane. The length of the stribng from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2
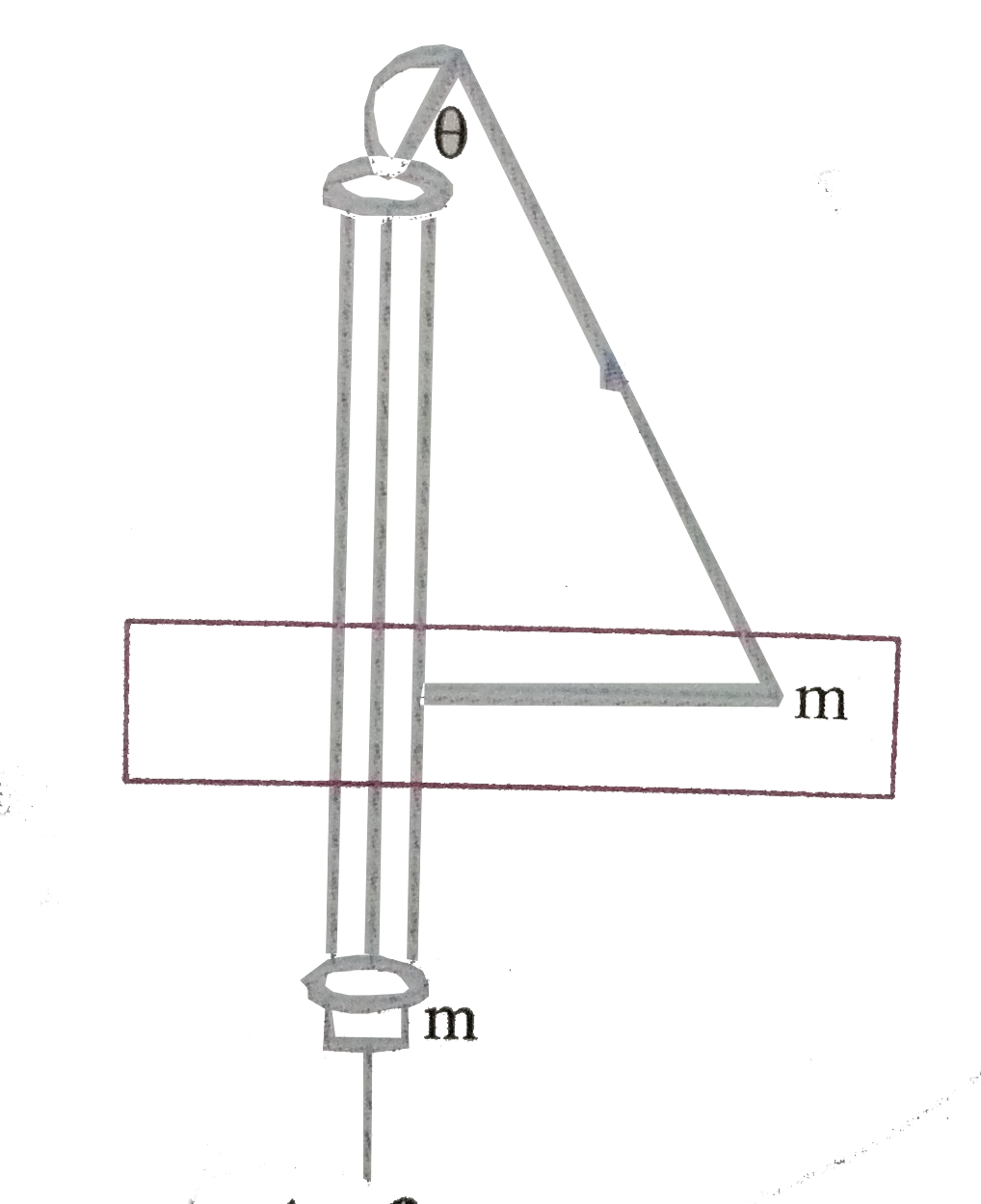
View SolutionA large mass M and a small mass m hang at the two ends of string passing through a smooth tube. The mass m moves around in a circular path in a horizontal plane. The length of the string from the mass m to the top of the tube of the tube is l and θ is the angle this length makes with the vertical. What should be the frequency of rotation of the mass m so that M remains stationary ?
View Solution
Knowledge Check
Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)gTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the aboveTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
 Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
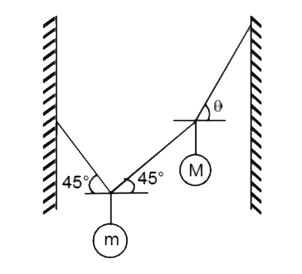
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibruim, then
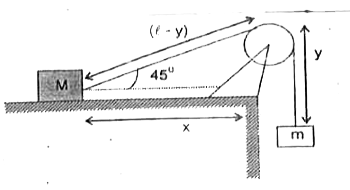
View SolutionTwo masses M and m are connected by a light inextensible string which passes over a small pulley as shown in the diagram. If the mass m is moving downward with a velocity v when the string makes an angle of 45∘ with the horizontal, find the total K.E. of the two masses. AsSigmae that the mass M moves horizontally.
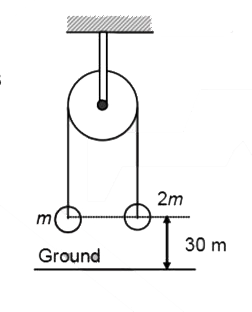
View SolutionTwo masses m and 2m are connected by a massless string, which passes over a pulley as shown in figure. The masses are held initially with equal lengths of the strings on either side of the pulley. Find the velocity of masses at the instant the lighter mass moves up a distance of 15m. ( g=10m/s2 )
View SolutionA bob of mass m is projected with a horizontal velocity v=√gl2 as shown in figure. In consequence, it moves in a circular path in a vertical plane by the inextensible string which passes over the smooth fixed peg. Find the maximum angle that the bob swings in the left hand side.
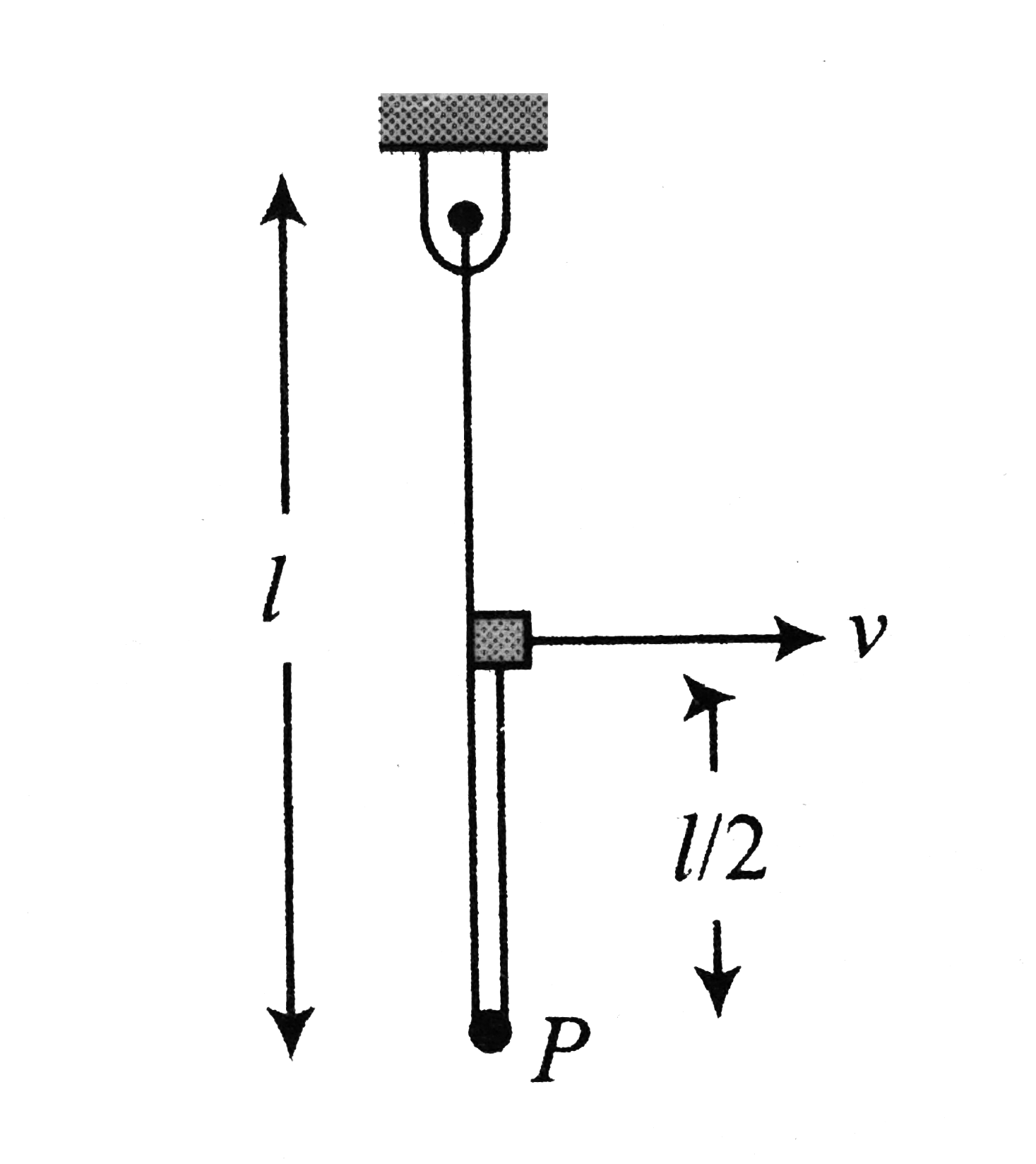
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
View Solution