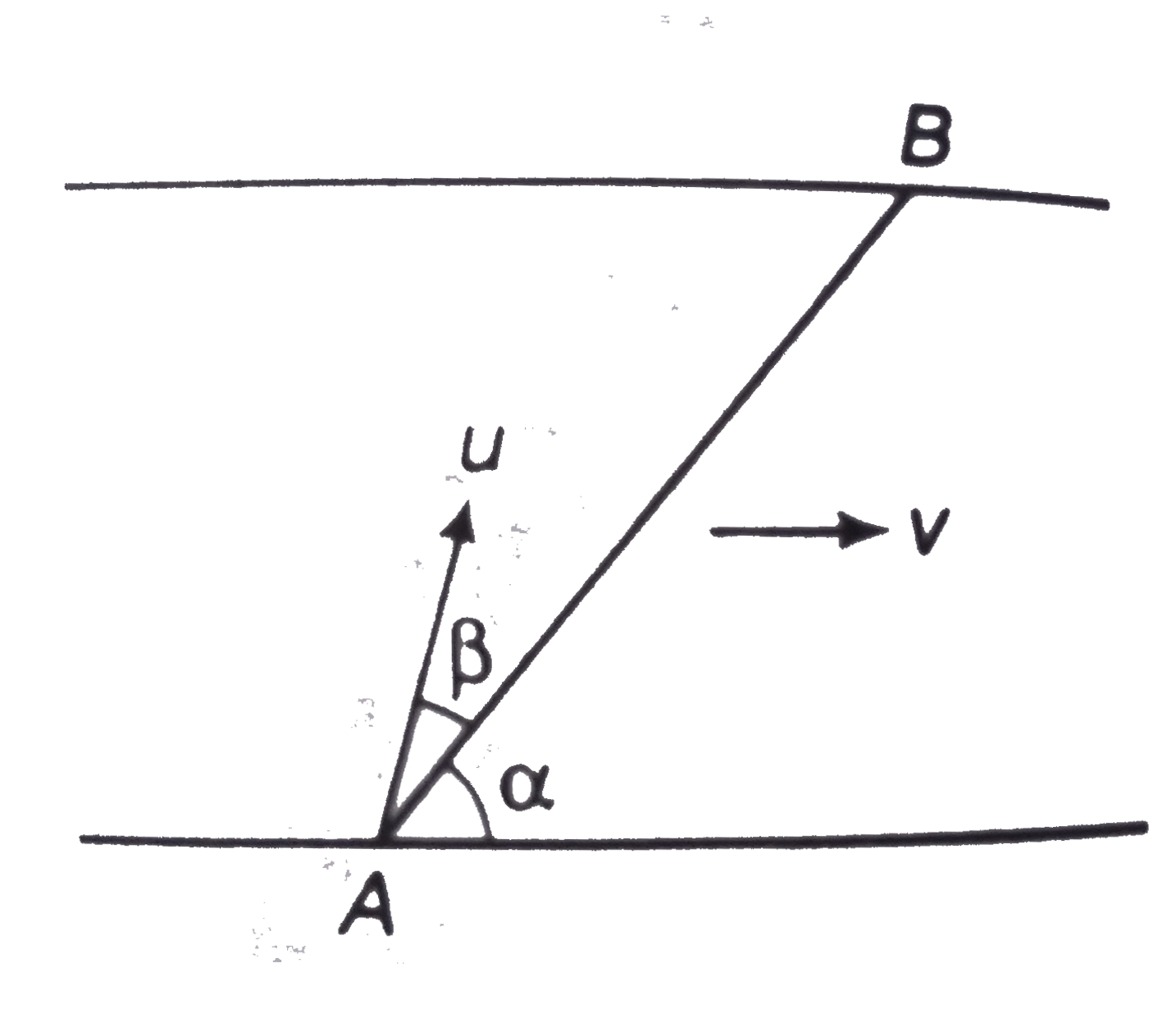
A launch plies between two points A and B on the opposite banks of a river always following the line AB. The distance S between points and B is 1200 m. The velocity of the river current v=1.9m/s is constant over the entire width of the river. The line AB makes an angle α=60∘ with the direction of the current. With what velocity u and at what angle beta to the line AB should the launch move to cover the distance AB and back in a time t=5min? The angle beta remains the same during the passage from A to B and from B to A.
The correct Answer is:A, B
In order that the moving launch is always on the
straight line AB, the components of velocity of the
current and of the launch in the direction
perpendicular to AB should be equal, i.e.
usinβ=vsinα ...(i)
S=AB=(ucosβ+vcosα)t1 ...(ii)
Further BA=(ucosβ−vcosα)t2 ...(iii)
t1+t2=t ...(iv)
Solving these equations after proper substitution,
we get
u=8m/sandβ=12∘
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE
39 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE
23 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
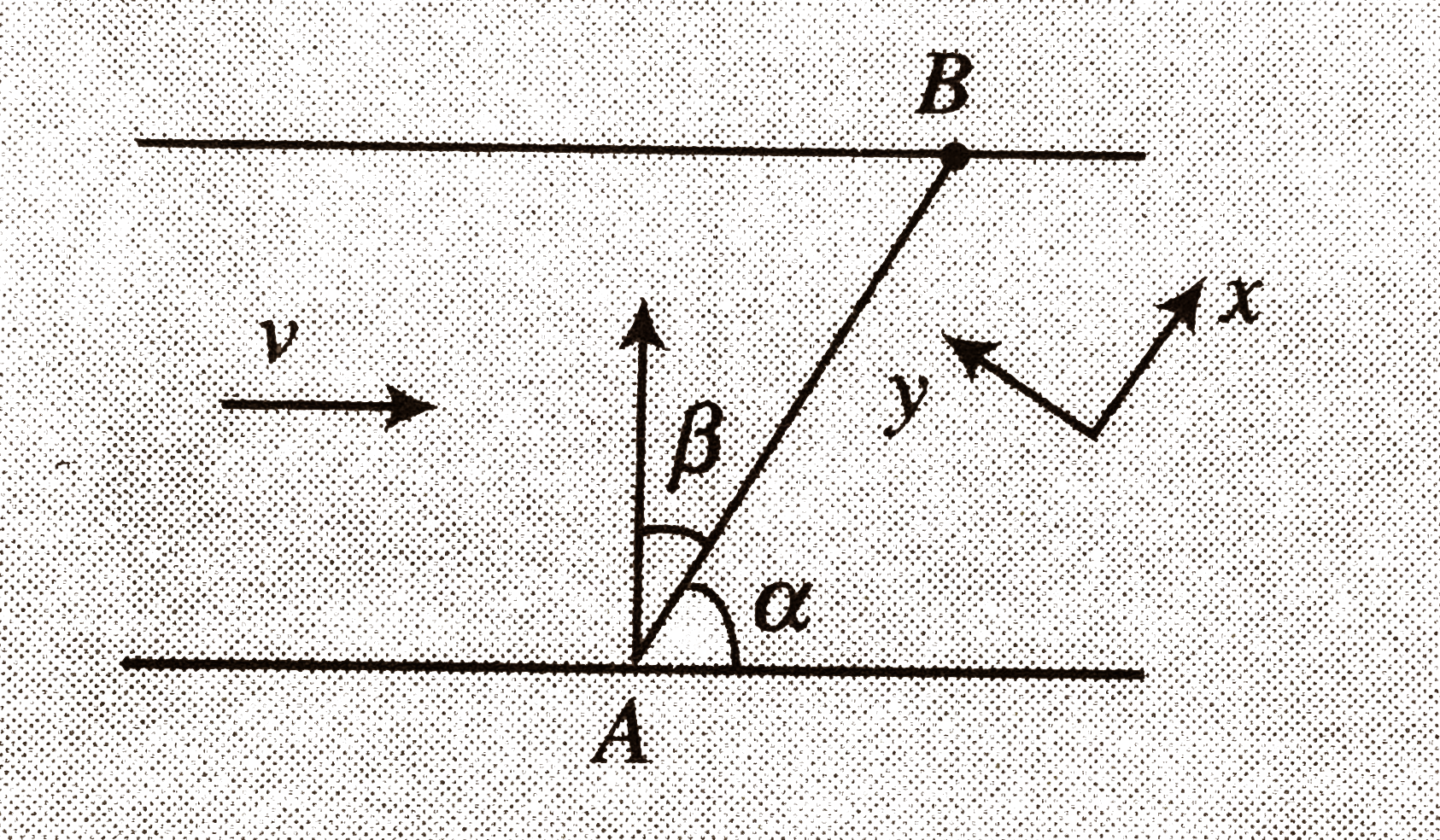 .
.
View SolutionTwo trees, A and B are on the same side of a river. From a point C in the river the distance of trees A and B are 25 m and 300 m respectively. If the angle C is 450 , find the distance between the trees (use √2=1.44)
View Solution
Knowledge Check
The distance between two points differing in phase by 60∘ on a wave, velocity 360 m./s and frequency 500 Hz is
A24 cmB12 cmC6 cmD1 cm
A swimmer wishes to reach directly opposite bank of a river, flowing with velocity 8 m/s. The swimmer can swim 10 m/s still water. The width of the river is 480 m. Time taken by him to do so:
View SolutionA person reaches on a point directly opposite on the other bank of a river.The velocity of the water in the river is 4m/sand the velocity of the person in still water is 5m/s.If the width of the river is 84.6m, time taken to cross the river in seconds is
View SolutionA person standing on the bank of a river observes that the angle subtended by a tree on the opposite of bank is 60∘. When he retires 40 m.from the bank, he finds the angle to be 30∘. What is the breadth of the river ?
View SolutionA boat moves perpendicular to the bank with a velocity of 7.2 km/h. The current carries it 150 m downstream, find the velocity of the current. (The width of the river is 0.5 km).
View SolutionVelocity of the boat with respect to river is 10 m/s. From point A it is steered in the direction shown to reach point C. Find the time of the trip and distance between B and C

View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionA river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View Solution
