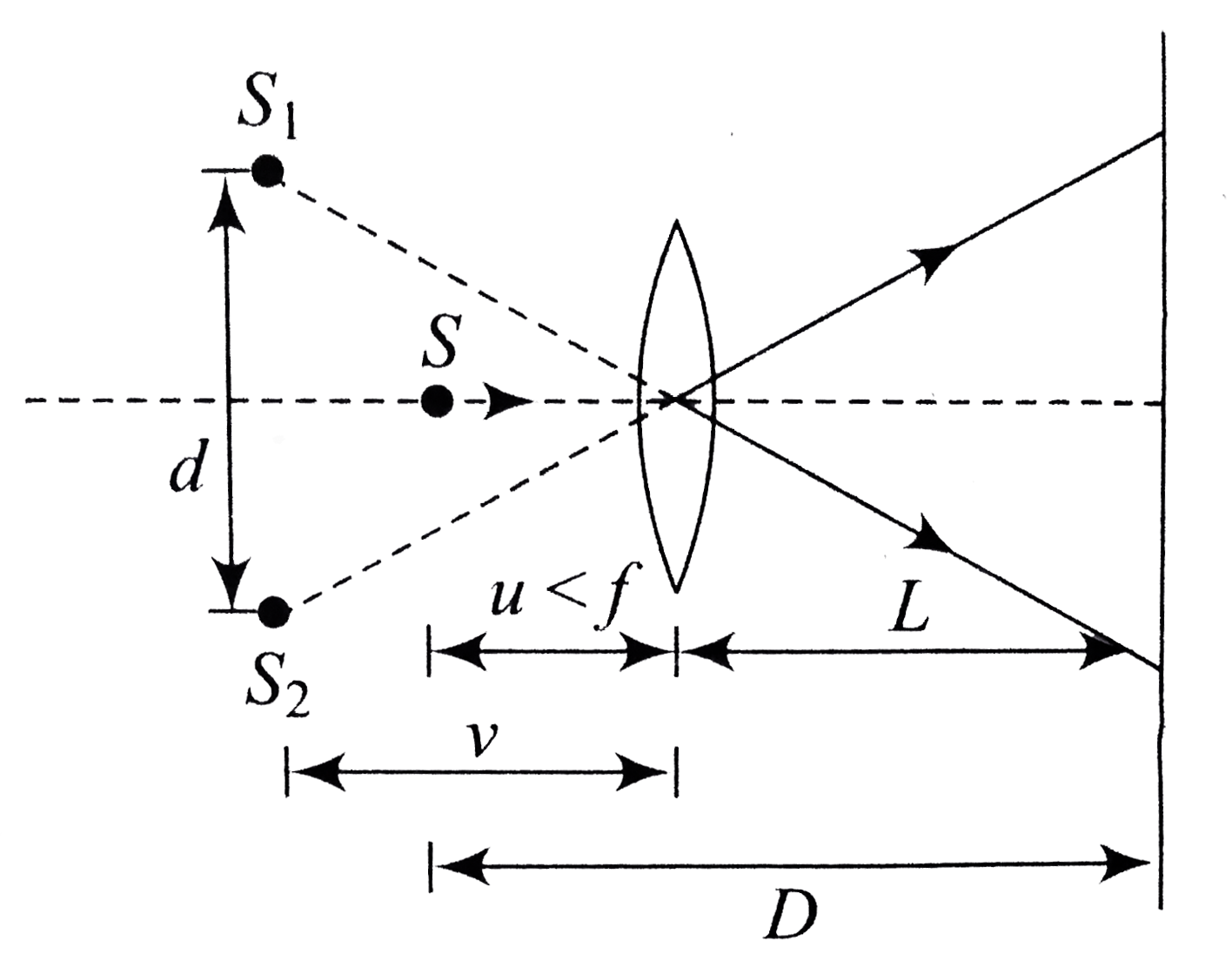
A lens of focal length f is cut along the diameter into two identical halevs. In this process, a layer of the lens t in thickness is lost, then the halves are put together to form a composite lens. In between the focal plane and the composite lens, a narrow slit is placed near the focal plane. The slit is emitting monochromatic λ. Behind the lens, a screen is located at a distance L front it.

Find the fringe width for the pattern obtained under given arrangement on the screen.
λf2t
λft
tfλ
tfλ2
The correct Answer is:b
From lens equation, we have
v=uff−u
d=2(12)[vu−1]=t[uf−u]
D=L+v=L+uff−u
Fringe width,
β=λDd=⎡⎢
⎢⎣λ[L+uff−u]t[uf−u]⎤⎥
⎥⎦
β=λt[f+L(f−u)u]
When u→f,β=λft
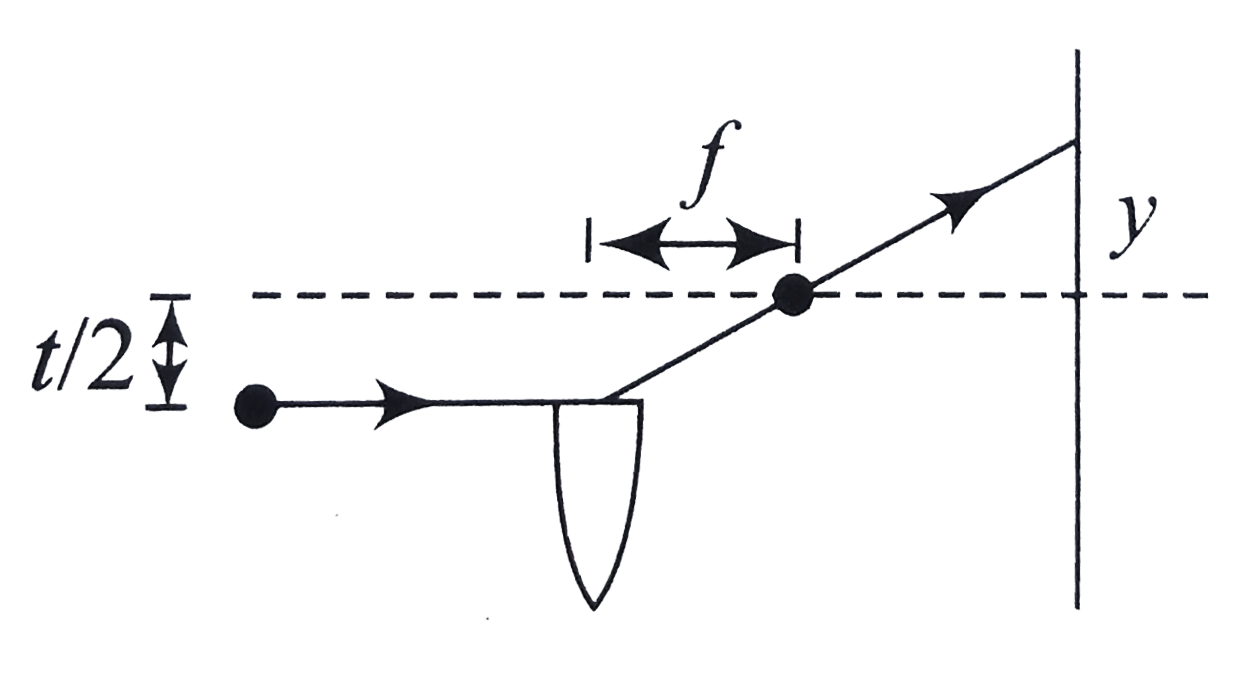
From the figure,
yL−f=t/2f⇒y=t/2f(L−f)
distance of the point up to which interference occurs,
y0=t/2f(L−f)+t2=tL2f
Number of visible maxima =tLt2f×λf=Lt22λf2
 .
.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
A lens of diameter 5.0cm and focal length f=25.0cm was cut along the diameter into two identical halves. In the process, the layer of the lens α=1.00mm in thieckness was lost. Then the halves were put together to form a composite lens. In this focal plane a narrow slit was placed, emitting monochromatic light with wavelength λ=0.60μm. Behind the lens a screen was located at a distance b=50cm from it. Find:
(a) the which of a fringe on the screen and the number of possible maxima,
(b) the maximum width of the slit ∂max at which the fringes on the screen will be still observed sufficiently sharp.
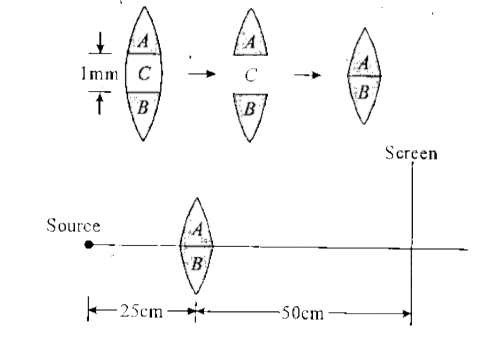
View SolutionIn Billet's Lens Arrangement, a convex lens of focal length 50 cm is cut along the diameter into two indentical halves Å and B and in the process a layer C of the lens thickness 1 mm is lost. Then the two halves A and B are put together to form a composite lens. Now, infront of this composite lens a source of light emitting wavelength λ=6000Å is placed at a distance of 25 cm as shown in the figure. Behind the lens there is a screen at a distance 50 cm from it. Find the fringe width fo the interference pattern obtained on the screen.
View Solution
Knowledge Check
A lens of focal length f is cut along the diameter into two identical halevs. In this process, a layer of the lens t in thickness is lost, then the halves are put together to form a composite lens. In between the focal plane and the composite lens, a narrow slit is placed near the focal plane. The slit is emitting monochromatic λ. Behind the lens, a screen is located at a distance L front it.
The expression for the number of visible maxima which are obtained through above said arrangement will turn out to beALt2λf2B2Lt2λf2CLt2λf2DLt22λf2
The focal length of the convex lens isA+10 cmB+20cmC−10cmD−20cmHow power of the lens in related to focal length of the lens ?
ADirectly proportional to fBDirectly proportional to 1fCDirectly propotional to √fDDirectly proportional to 1f2
Define focal length of a lens.
View SolutionThe focal length of a convex lens is
View SolutionAn equiconvex lens of focal length 15cm is cut into two equal halves in thickness. What is the focal length of each half ?
View SolutionA diverging lens of focal length F is cut into two idential parts, each forming a plano concave lens, Fig. What is the focal length of each part ?

View SolutionA convex lens of focal length f cut into parts first horizontally and then vertically. Find the focal length of part A of the lens, as shown:
View Solution
