A liquid of density ρ is filled upto a geight of 'h' in a container as shown in firgure. Base of the contaimer is a square of side L. Ignoring the atmospheric pressure find

(a) pressure force F1 on its base.
(b) torque of force F1 about an axis passing through C and perpendicular to plane of paper.
(c) Pressure force F2 on the vertical side wall DC.
(d) torque of force F2 about the same axis mentioned in part (b).
(e) point of application of force F2
(a) Base is horizontal. So, we can directy apply
F1=pA=(ρgh)(L)(L)
=ρghL2
(b) Point of application of F1 is at a perpendicular distance L2 from the axis mentioned in the question
∴τF1=F1×r⊥=(ρghL2)(L2)
=12ρghL3
(c) and (d) : side wall is vertical. Pressure is non-uniform. so, force and torque both will be obtained by integration.
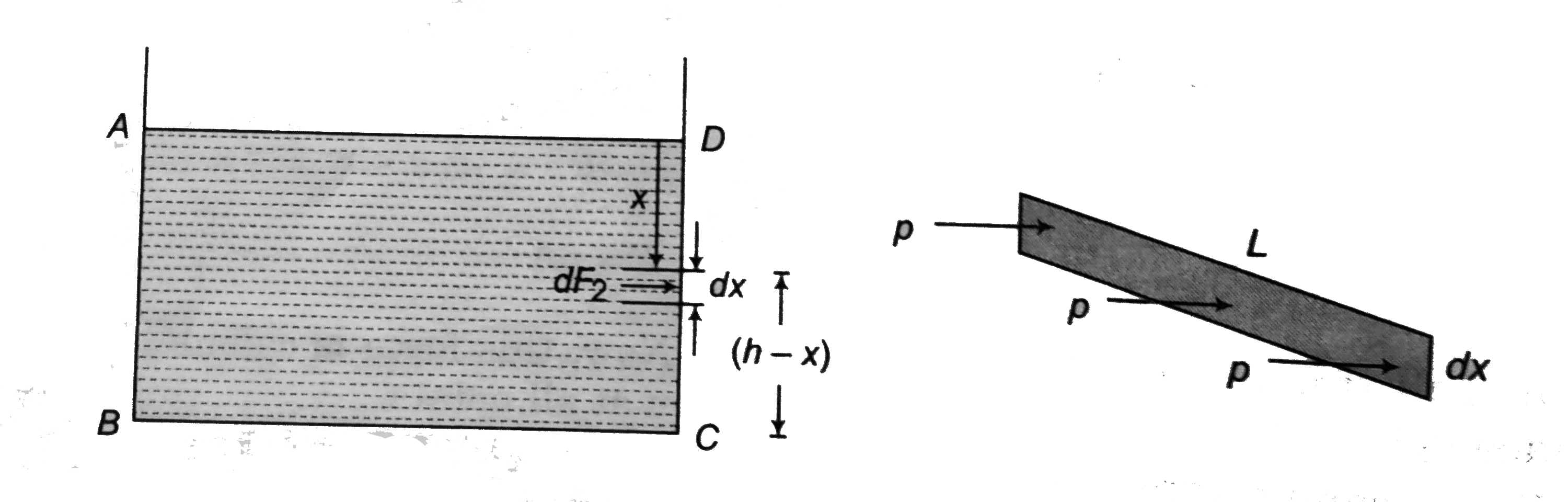
Pressure at depth x,
p=ρgx
Area of small element shown in figure is
dA=L(dx)
∴dF2=(p)(dA)=(ρgx)(Ldx)
Perpendicular distance of this small force dF2 from the axis mentioned in the question is (h−x). Therefore, small torque of force dF2 is
dτ=(dF2)(h−x)
=(ρgx)(h−x)(Ldx)
Now, F2−∫x=hx=0dF2
τF2=∫x=hx=0(dτ)
Substituting the value and then integration, we get
F2=ρgLh22
and τF2=ρgLh36
(e) For point of application of F2, we can apply
r⊥=τF2F2 (from C)
=(ρgLH3/6)(ρgH2L/2)=h3
Note that point of application of F2 is below the centre, as pressure is not uniform. It is increasing with depth.
F1 and F2 and their points of application are shown in figure below.
 .
.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples
10 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.1
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
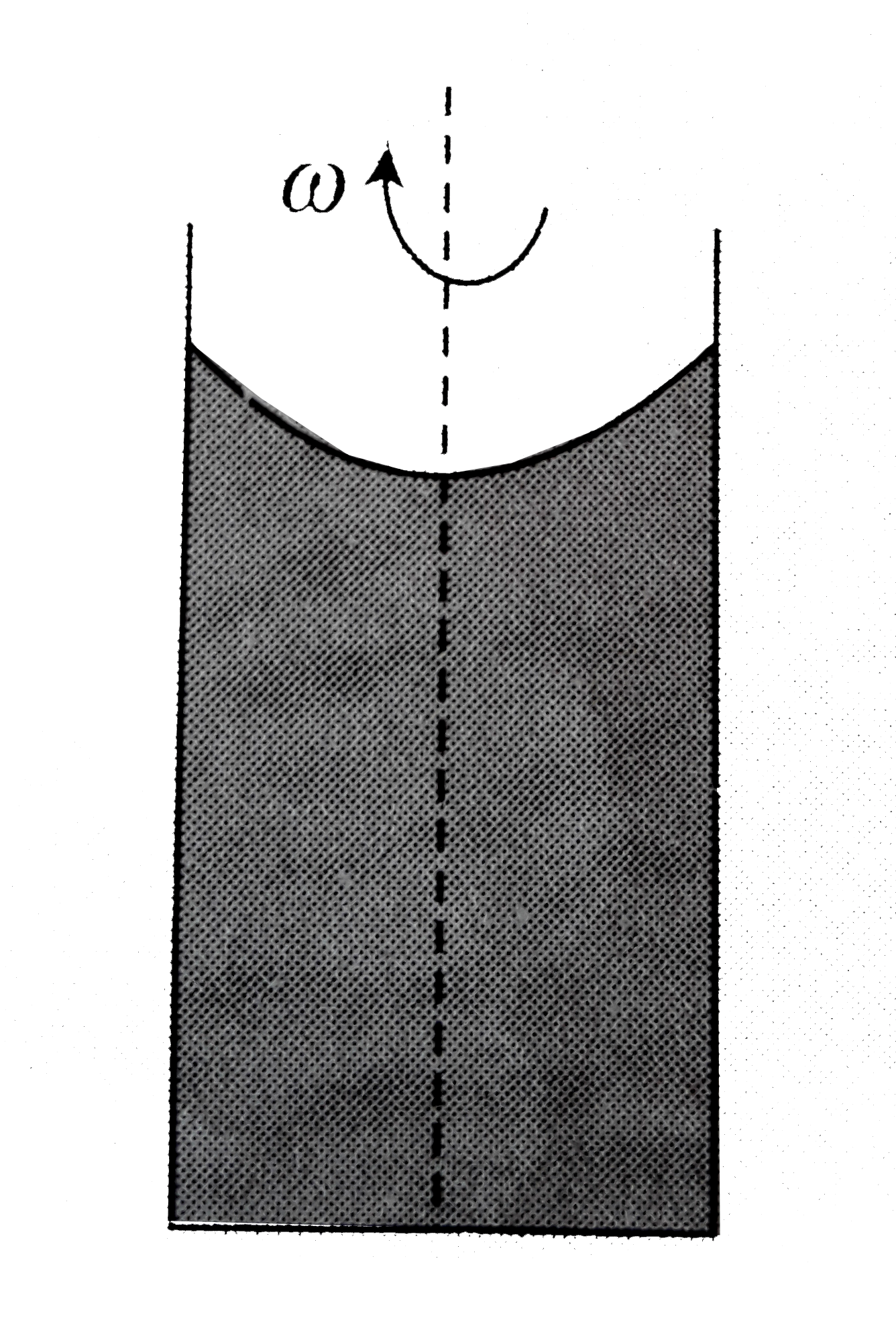
A liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
 .
.
View SolutionA liquid of density ρ is filled in a beaker of cross section A to a height H and then a cylinder of mass M and cross-section a is made to float in it as shown in

If the atmospheric pressure is P0 find the pressure (a) at the top face B of the cylinder (b) at the bottom face C of the cylinder and (c ) at the base D of the beaker. (d) Can ever these pressure be equal ?
View Solution
Knowledge Check
A container shown in figure contains a liquid to depth H, and of density ρ The gauge pressure at point P is :
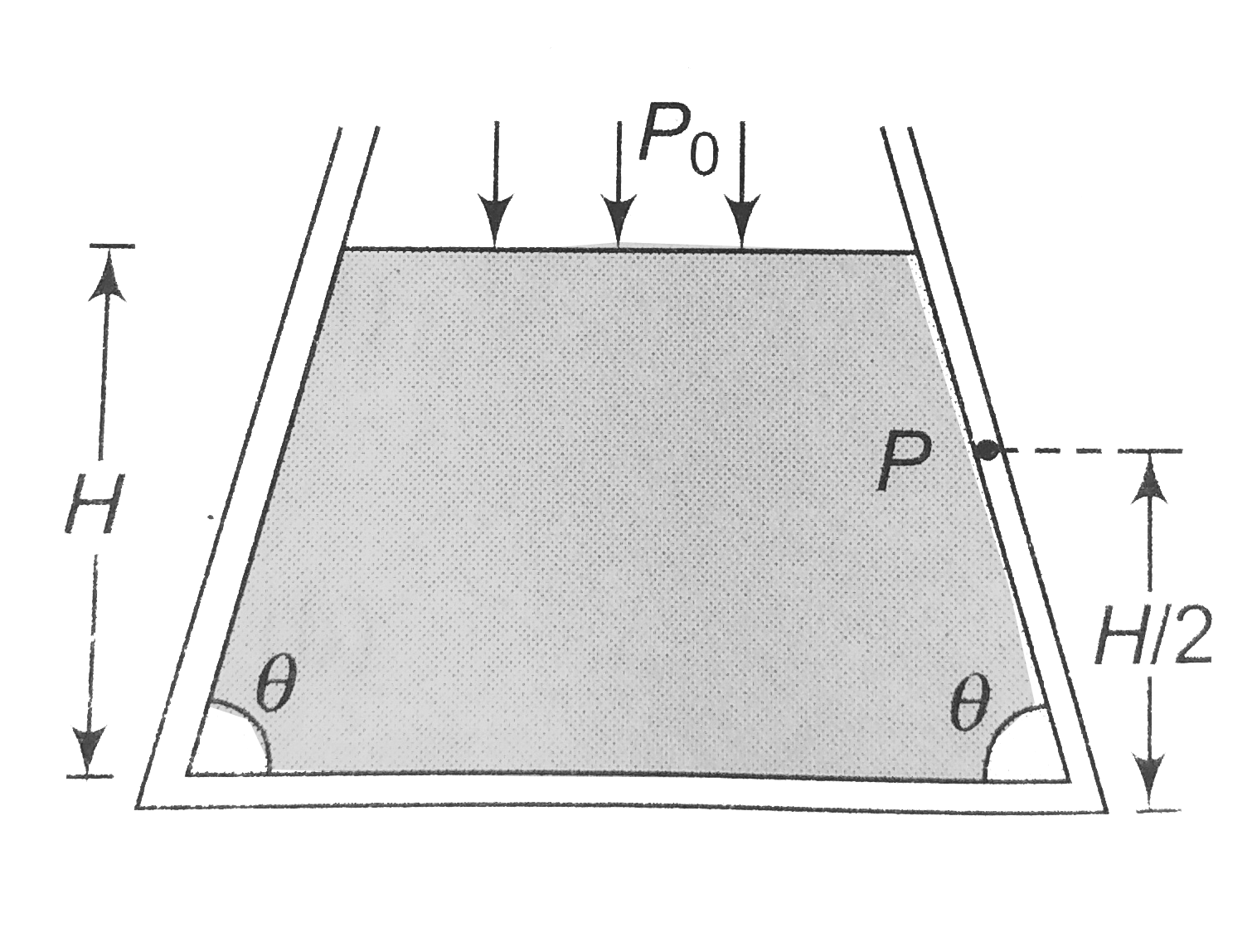 AρgH2+P0BρgH2CρgH2cosθDρgHcosθ2
AρgH2+P0BρgH2CρgH2cosθDρgHcosθ2A liquid of mass 1 kg is filled in a flask as shown in figure. The force exerted by the flask on the liquid is (g=10m/s2) [Neglect atmospheric pressure]:
 A10 NBgreater than 10NCless than 10NDzero
A10 NBgreater than 10NCless than 10NDzeroA beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
A0BhρgChρg3D2hρg
Find the position of the centre of two unequal antiparallel forces. The distance between the points of application of the forces F1 and F2 is a.
View SolutionThe pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
View SolutionPressure exerted by a liquid on the base of the container is due to its :
View SolutionForces F1andF2 act on a point mass in two mutually perpendicular directions. The resultant force on the point mass will be
View SolutionIf F is a force acting normally on a surface of area A, then the pressure P is given by
View Solution
