A long charged cylinder of linear charge density $λ$ surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders?

Text Solution

Verified by Experts

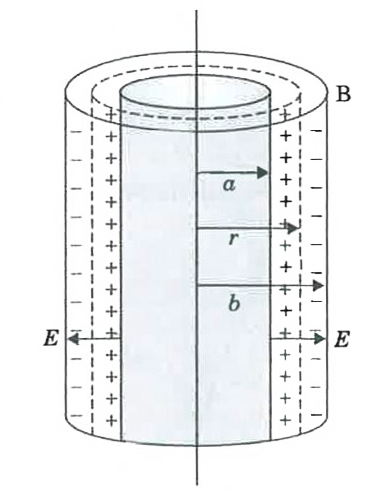
As the charged cylinder is surrounded by the coaxial conducting cylinder, it will induce charge on the conducting cylinder. The electric field in between due to the charged cylinder will be directed radially outwards and perpendicular to the axis of the cylinder
Let us take a Gaussian surface in the form of a closed cylinder of radius r and length $l$ that is coaxial to the charged cylinder and lying in between the two cylinders.
Let E be the magnitude of the electric field intensity in the space between the two cylinders. Flux associated with lower and upper circular faces of the Gaussian surface will be zero as the electric field lines are parallel to these surfaces.
Electric flux associated with the Gaussian cylinder,
$ϕ = \int_{cylinder} \to E . d \to S = E (2 π r l)$
According to Gauss.s law the total flux for a three-dimensional, closed Gaussian surface, is equal to net charge enclosed within surface divided by $ε_{0}$ .
$\Rightarrow E (2 π r l) = \frac{λ l}{ε_{0}} \Rightarrow E = \frac{λ}{2 π ε_{0} r}$

Updated on:21/07/2023

A very long uniformly charged cylinder (radius R) has a surface charge density $σ$ . A very long uniformly charged line charge( linear charge density $λ$ ) is placed along the cylinder axis. If electric field intensity vector outside the cylinder is zero then :
A $λ = R σ$
B $λ = - R σ$
C $λ = 2 π R σ$
D $λ = - 2 π R σ$
Two parallel infinite line charges with linear charge densities $+ λ C / m$ and $- λ$ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
A $\frac{λ}{2 π ε_{0} R} N / C$
Bzero
C $\frac{2 λ}{π ε_{0} R} N / C$
D $\frac{λ}{π ε_{0} R} N / C$