A long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point (a) just inside the tube (b) just outside the tube.
To solve the problem of finding the magnetic field at a point just inside and just outside a long cylindrical tube carrying a uniformly distributed current, we will use Ampere's Law. Let's break down the solution step by step.
Step 1: Understanding the Geometry
We have a long cylindrical tube with inner radius a and outer radius b. The current I is uniformly distributed over the cross-section of the tube, which means it flows through the material between the inner and outer radii.
Step 2: Calculate the Current Density
The current density J can be calculated using the formula:
J=IA
where A is the cross-sectional area of the tube. The area A of the cross-section can be calculated as:
A=π(b2−a2)
Thus, the current density becomes:
J=Iπ(b2−a2)
Step 3: Finding the Magnetic Field Just Inside the Tube
To find the magnetic field just inside the tube (at radius a), we apply Ampere's Law:
∮B⋅dl=μ0Iin
where Iin is the current enclosed by the Amperian loop. Since we are considering a point just inside the tube where there is no current flowing (the current is only in the material of the tube), we have:
Iin=0
Thus, applying Ampere's Law:
∮B⋅dl=0
This implies that the magnetic field B just inside the tube is:
Binside=0
Step 4: Finding the Magnetic Field Just Outside the Tube
Next, we find the magnetic field just outside the tube (at radius b). Again, we apply Ampere's Law:
∮B⋅dl=μ0Iin
In this case, the entire current I is enclosed by the Amperian loop, so:
Iin=I
The path length dl around the loop is 2πb, thus:
B⋅2πb=μ0I
Solving for B:
Boutside=μ0I2πb
Final Answers
- The magnetic field just inside the tube is:
Binside=0
- The magnetic field just outside the tube is:
Boutside=μ0I2πb
We have a long cylindrical tube with inner radius a and outer radius b. The current I is uniformly distributed over the cross-section of the tube, which means it flows through the material between the inner and outer radii.
The current density J can be calculated using the formula:
J=IA
where A is the cross-sectional area of the tube. The area A of the cross-section can be calculated as:
A=π(b2−a2)
Thus, the current density becomes:
J=Iπ(b2−a2)
To find the magnetic field just inside the tube (at radius a), we apply Ampere's Law:
∮B⋅dl=μ0Iin
where Iin is the current enclosed by the Amperian loop. Since we are considering a point just inside the tube where there is no current flowing (the current is only in the material of the tube), we have:
Iin=0
Thus, applying Ampere's Law:
∮B⋅dl=0
This implies that the magnetic field B just inside the tube is:
Binside=0
Next, we find the magnetic field just outside the tube (at radius b). Again, we apply Ampere's Law:
∮B⋅dl=μ0Iin
In this case, the entire current I is enclosed by the Amperian loop, so:
Iin=I
The path length dl around the loop is 2πb, thus:
B⋅2πb=μ0I
Solving for B:
Boutside=μ0I2πb
- The magnetic field just inside the tube is:
Binside=0
- The magnetic field just outside the tube is:
Boutside=μ0I2πb
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 27videos
MAGNETIC FIELD DUE TO CURRENT
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer6videos
MAGNETIC PROPERTIES OF MATTER
Similar Questions
A long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
View SolutionA long cylinder of wire of radius 'a' carries a current i distributed uniformly over its cross section. If the magnetic fields at distances r<aandR>a from the axis have equal magnitude, then
View SolutionA thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionFigure shows a cylindrical conductor of inner radius a & outer radius b which carries a current i unifromly spread over its cross section.Show that the magnetic field B for points inside the body of the conductor (i.e. a<r<b) is given by. B=μ0i2π(b2−a2)r2−a2r.Check this formula for the limiting case of a=0.
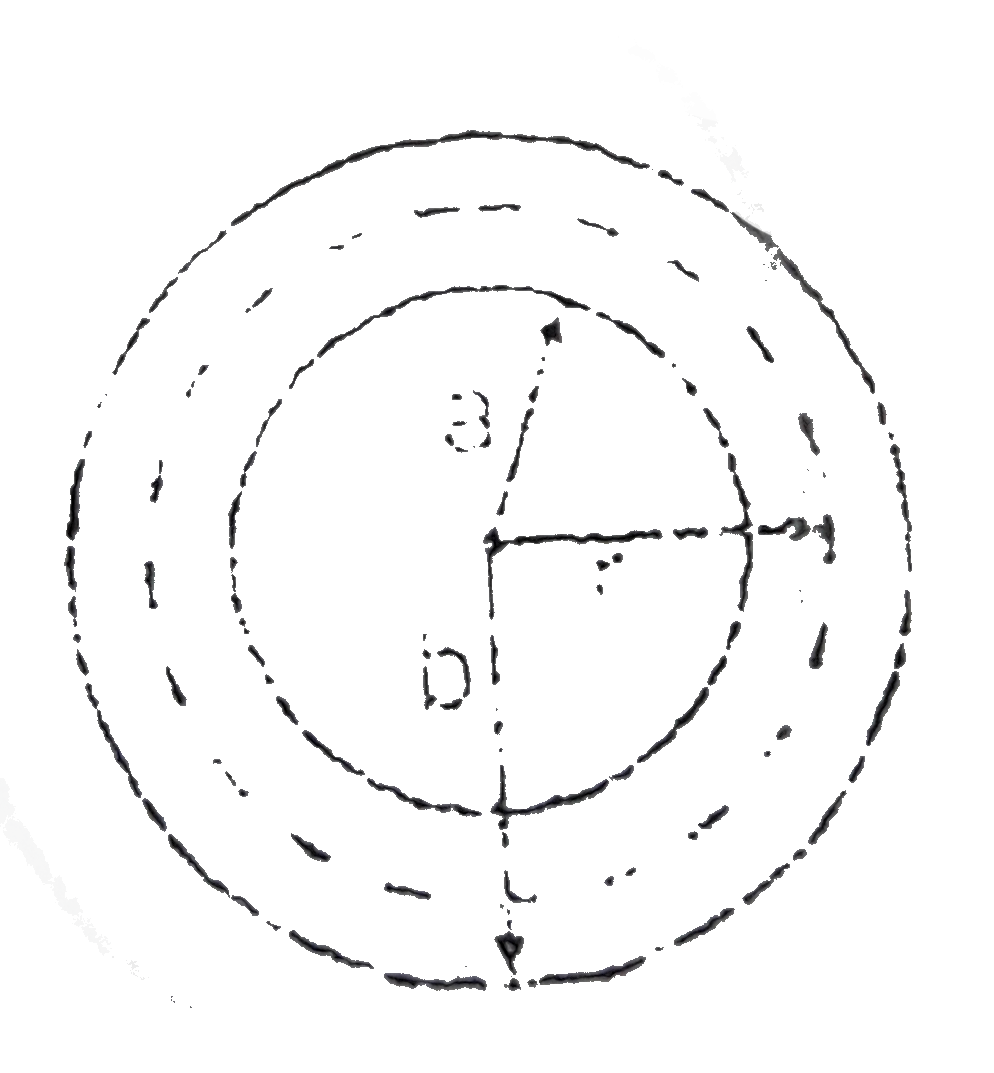 View Solution
View SolutionA solid wire of radius 10 cm carries a current of 5.0 A distributed uniformly over its cross section. Find the magnetic field B at a point at a distance (a) 2 cm (b) 10 cm and (c) 20 cm away from the axis.
View SolutionA 10 cm long rod carries a charge of +150μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both the ends of the rod.
View SolutionStatement-1 Magnetic force is always onon-central while the electric force may be central
Statement-2 magnetic field can acclerate a charged particle
Statement-3 Consider a long, straight wire of radius R, carrying a current distributed uniformly over its cross-section. The magnitude of the magnetic field is maximum at surface of the wire.View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View Solution

