A long horizontal metallic rod with length along the east-west direction is falling under gravity. The potential difference between its two ends will
be zero
be constant
increase with time
decrease with time
The correct Answer is:C
To solve the problem of finding the potential difference between the two ends of a long horizontal metallic rod falling under gravity, we can follow these steps:
Step 1: Understand the Setup
We have a long metallic rod oriented in the east-west direction and it is falling vertically under the influence of gravity. The falling motion of the rod will induce an electromotive force (EMF) due to its motion through the Earth's magnetic field.
Hint: Identify the orientation of the rod and the direction of the gravitational force acting on it.
Step 2: Identify the Relevant Formula
The induced EMF (ε) in a conductor moving through a magnetic field can be given by the formula:
EMF=B⋅L⋅v
where:
- B is the magnetic field strength,
- L is the length of the rod,
- v is the velocity of the rod.
Hint: Recall that EMF is related to the magnetic field, the length of the conductor, and its velocity.
Step 3: Determine the Velocity of the Rod
As the rod falls under gravity, its velocity v increases over time. The velocity can be expressed using the equations of motion:
v=u+gt
Since the initial velocity u=0 (the rod starts from rest), we have:
v=gt
Hint: Use the equations of motion to express the velocity of the falling rod.
Step 4: Substitute the Velocity into the EMF Formula
Substituting v=gt into the EMF formula gives us:
EMF=B⋅L⋅(gt)
This indicates that the induced EMF is directly proportional to time t.
Hint: Substitute the expression for velocity into the EMF formula to see how it changes over time.
Step 5: Conclusion about the Potential Difference
Since the EMF is proportional to time, it means that the potential difference between the two ends of the rod increases as the rod continues to fall. Therefore, the potential difference will increase with time.
Hint: Analyze the relationship between EMF and time to conclude about the behavior of the potential difference.
Final Answer
The potential difference between the two ends of the rod will increase with time.
We have a long metallic rod oriented in the east-west direction and it is falling vertically under the influence of gravity. The falling motion of the rod will induce an electromotive force (EMF) due to its motion through the Earth's magnetic field.
The induced EMF (ε) in a conductor moving through a magnetic field can be given by the formula:
EMF=B⋅L⋅v
where:
- B is the magnetic field strength,
- L is the length of the rod,
- v is the velocity of the rod.
As the rod falls under gravity, its velocity v increases over time. The velocity can be expressed using the equations of motion:
v=u+gt
Since the initial velocity u=0 (the rod starts from rest), we have:
v=gt
Substituting v=gt into the EMF formula gives us:
EMF=B⋅L⋅(gt)
This indicates that the induced EMF is directly proportional to time t.
Since the EMF is proportional to time, it means that the potential difference between the two ends of the rod increases as the rod continues to fall. Therefore, the potential difference will increase with time.
The potential difference between the two ends of the rod will increase with time.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A horizontal straight conductor when placed along south-north direction falls under gravity, there is
View SolutionState Lenz's Law.
A metallic rod held horizontally along east-west direction, is allowed to fall under gravity. Will there be an emf induced at its ends? Justify your answer.View SolutionSTATEMENT - 1 : The magnetic flux through a closed surface is zero.
STATEMENT - 2 : When a rod oriented along magnetic north and magnetic south direction falls under gravity. Potential difference developed across its ends is zero.
STATEMENT - 3 : A resistance is connected to an ac source. If an inductor is included in the circuit in series. The average power dissipated in the resistance will decrease.View SolutionA conducing rod of length l is falling with a velocity v perpendicular to a unifrorm horizontal magnetic field B . The potential difference between its two ends will be
View SolutionA conducting rod AB of lemgth 2 l moves through a uniform magnetic field B. The rod makes an angle θ with the vertical while it falls with a uniform linear velocity v. The potential difference between the two ends of the rod is Bv2l .
 View Solution
View SolutionA conducting rod of length l is hinged at point O. It is a free to rotate in a verical plane. There exists a uniform magnetic field B in horizontal direction. The rod is released from the position shown. The potential difference between the two ends of the rod is proportional to
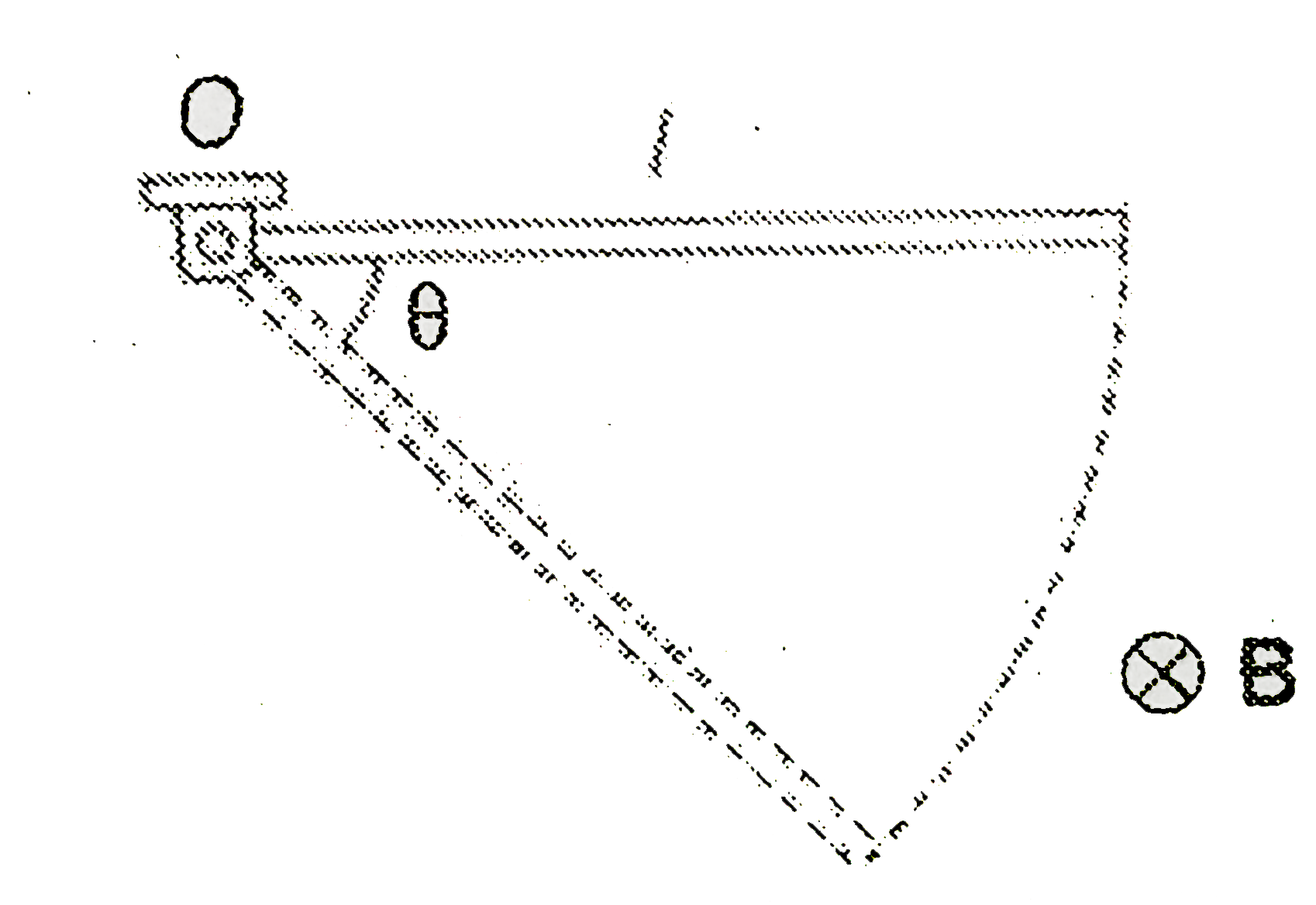 View Solution
View SolutionA metal rod of length L is placed normal to a magnetic field and rotated through one end of rod in circular path with frequency f. The potential difference between it ends will be-
View SolutionA metallic rod of length I rotates at angular velocity ω about an axis passing through one end and perpendicular to the rod. If mass of electron is m and its charge is -e then the magnitude of potential difference between its two ends is
View Solutionthe following table gives the lengths of four copper rods at the temperature ,their diameters and the potential differences between their ends.
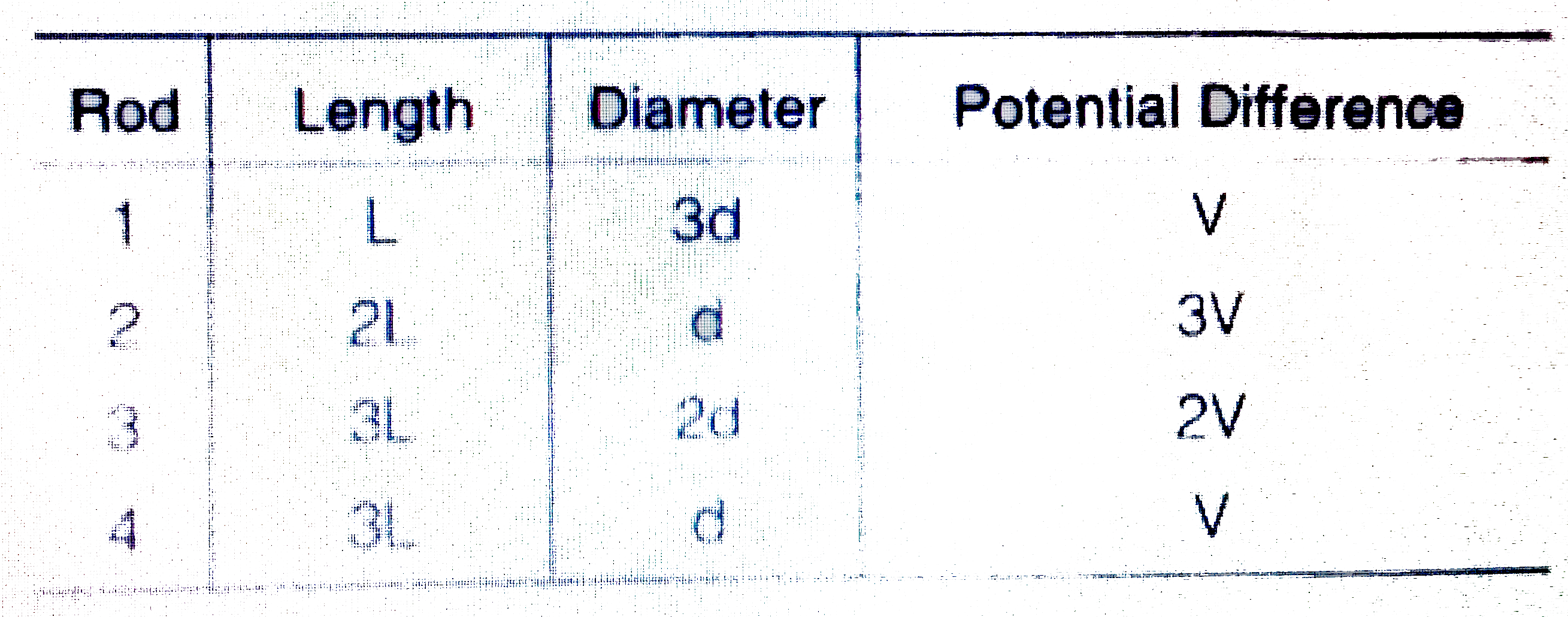
 View Solution
View SolutionA rod of length 20 cm is rotating with angular speed of 100 rps in a magnetic field of strength 0.5 T about it’s one end . What is the potential difference betweet two ends of the rod :
View Solution

