A long solenoid is fabricated by closely winding a wire of radius 0.5 mm over a cylindrical nonmagnetic frame so that the successive turns nearly touch each other. What would be the magnetic field B at the centre of the solenoid if it carries a current of 5 A?
To find the magnetic field B at the center of a long solenoid carrying a current of 5 A, we can follow these steps:
Step 1: Identify the given parameters
- Radius of the wire r=0.5mm=0.5×10−3m
- Current I=5A
Step 2: Calculate the diameter of the wire
The diameter d of the wire is given by:
d=2r=2×0.5mm=1mm=1×10−3m
Step 3: Determine the number of turns per unit length n
Since the turns of the wire nearly touch each other, the number of turns per unit length n can be calculated as the reciprocal of the diameter:
n=1d=11×10−3m=103turns/m
Step 4: Use the formula for the magnetic field in a long solenoid
The magnetic field B inside a long solenoid is given by the formula:
B=μ0nI
where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
Step 5: Substitute the values into the formula
Substituting the values of μ0, n, and I into the equation:
B=(4π×10−7T m/A)×(103turns/m)×(5A)
Step 6: Calculate the magnetic field
Calculating the expression:
B=4π×10−4T
Now, substituting π≈3.14:
B≈4×3.14×10−4=12.56×10−4T=1.256×10−3T
Step 7: Final answer
Thus, the magnetic field B at the center of the solenoid is:
B≈1.256×10−3T or 6.28×10−3T
- Radius of the wire r=0.5mm=0.5×10−3m
- Current I=5A
The diameter d of the wire is given by:
d=2r=2×0.5mm=1mm=1×10−3m
Since the turns of the wire nearly touch each other, the number of turns per unit length n can be calculated as the reciprocal of the diameter:
n=1d=11×10−3m=103turns/m
The magnetic field B inside a long solenoid is given by the formula:
B=μ0nI
where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
Substituting the values of μ0, n, and I into the equation:
B=(4π×10−7T m/A)×(103turns/m)×(5A)
Calculating the expression:
B=4π×10−4T
Now, substituting π≈3.14:
B≈4×3.14×10−4=12.56×10−4T=1.256×10−3T
Thus, the magnetic field B at the center of the solenoid is:
B≈1.256×10−3T or 6.28×10−3T
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A solenoid consists of 100 turns of wire and has a length of 10 cm. The magnetic field inside the solenoid when it carries a current of 0.5 A will be :
View SolutionMagnetic field intensity at the centre of coil of 50 turns, radius 0.5m and carrying a current of 2A is
View SolutionA solenoid 50 cm long has 4 layers of windings of 350 turns each. If the current carried is 6A. Find the magnetic field at the centre of the solenoid
View SolutionA long solenoid is made by closely winding turns of wire of diameter d (together with insulation) (Fig. 27.5). The wire carries a current i. Find the magnetic field induction in the centre O and on the end A of the solenoid. out the calculation for d =0.1 mm, i =5 A.

View SolutionA long solenoid of 50 cm length having 100 turns carries a current of 2.5A. The magnetic field at centre of solenoid is:
View SolutionThree identical long solenoids P,Q and R are connected to each other as shown in figure . If the magnetic field at the centre of P is 2.0 T, what would be the field at the centre of Q? Assume that the field due to any solenoid is confined within the volume of that solenoid only.

View SolutionThree identical long solenoid P,Q and R are connected to each other as shown in fig. If the magnetic field at the centre of P is 2.0T, what would be the field (inT) at the centre of Q? Assume that the field due to any solenoid is confined within the volume of that solenoid only.
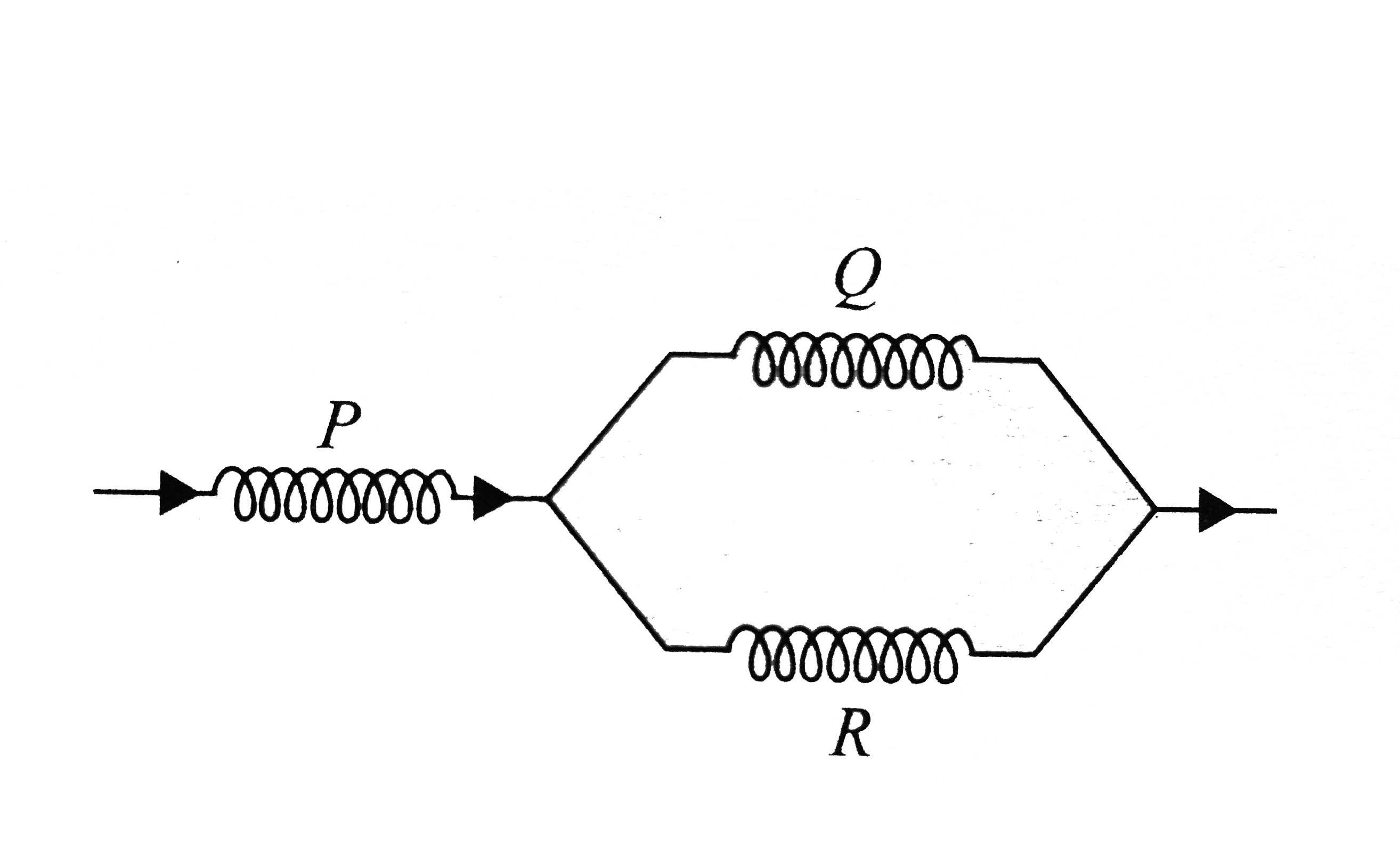
View SolutionCalculate magnetic flux density of the magnetic field at the centre of a circular coil of 50 turns, having radius of 0.5 m and carrying a current of 5A.
View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View SolutionA solenoid of 2m long & 3cm diameter has 5 layers of winding of 500 turns per metre length in each layer & carries a current of 5A. Find intensity of magnetic field at the centre of the solenoid.
View Solution
