A long, straight wire carries a current. Is Ampere's law
valid for a loop that does not enclose the wire, or that
encloses the wire but is not circular?
To solve the question regarding the validity of Ampere's law for different types of loops around a long straight wire carrying current, we can break it down into two parts:
Step 1: Understanding Ampere's Law
Ampere's law states that the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current I enclosed by the loop. Mathematically, it is expressed as:
∮B⋅dl=μ0Ienclosed
Step 2: Case 1 - Loop that does not enclose the wire
In the first scenario, we consider a loop that does not enclose the wire. Since the loop does not encircle any current, the enclosed current Ienclosed is zero. Therefore, according to Ampere's law:
∮B⋅dl=μ0⋅0=0
This implies that the integral of the magnetic field around the loop is zero. Hence, Ampere's law is not valid for this case because it does not provide any useful information about the magnetic field in the region outside the wire.
Step 3: Case 2 - Loop that encloses the wire but is not circular
In the second scenario, we consider a loop that does enclose the wire, even if it is not circular (for example, a rectangular loop). In this case, the loop encloses a current I. According to Ampere's law, we can still apply it:
∮B⋅dl=μ0Ienclosed
Here, Ienclosed is the current flowing through the wire, which is non-zero. Therefore, Ampere's law is valid for this loop, and we can calculate the magnetic field around the wire using this law.
Conclusion
1. For a loop that does not enclose the wire: Ampere's law is not valid.
2. For a loop that encloses the wire but is not circular: Ampere's law is valid.
Ampere's law states that the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current I enclosed by the loop. Mathematically, it is expressed as:
In the first scenario, we consider a loop that does not enclose the wire. Since the loop does not encircle any current, the enclosed current Ienclosed is zero. Therefore, according to Ampere's law:
In the second scenario, we consider a loop that does enclose the wire, even if it is not circular (for example, a rectangular loop). In this case, the loop encloses a current I. According to Ampere's law, we can still apply it:
1. For a loop that does not enclose the wire: Ampere's law is not valid.
2. For a loop that encloses the wire but is not circular: Ampere's law is valid.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
60 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5T
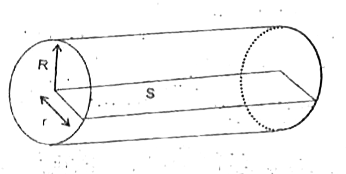
A long copper wire carries a current of 10 ampere . Calculate the magnetic flux per metre of the wire for a plane surface S inside the wire as shown in the figure.
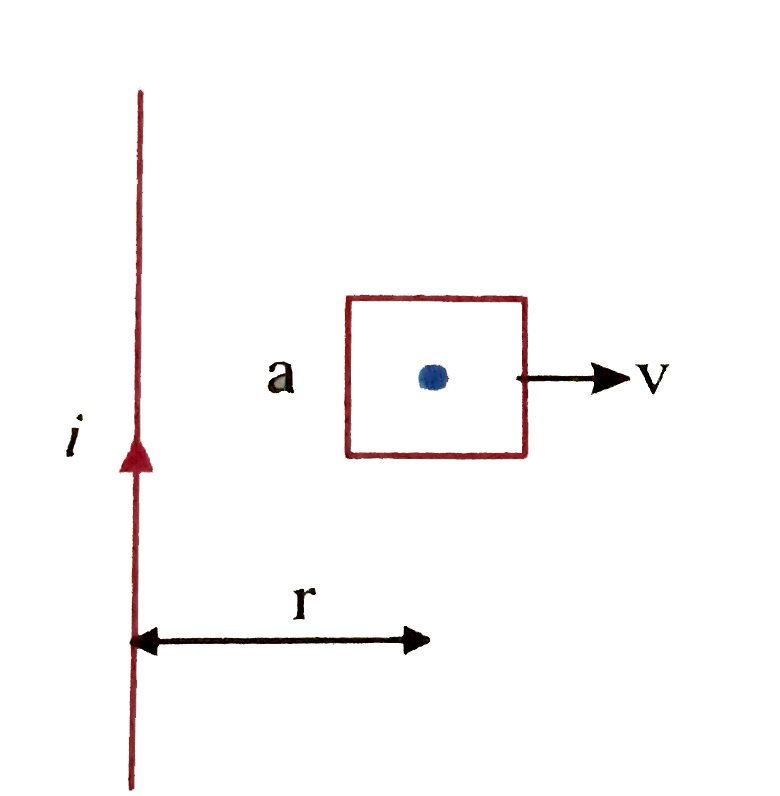
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
View SolutionA long straight wire of circular cross- section carries a current along its length. On the axis inside the wire, it follows that
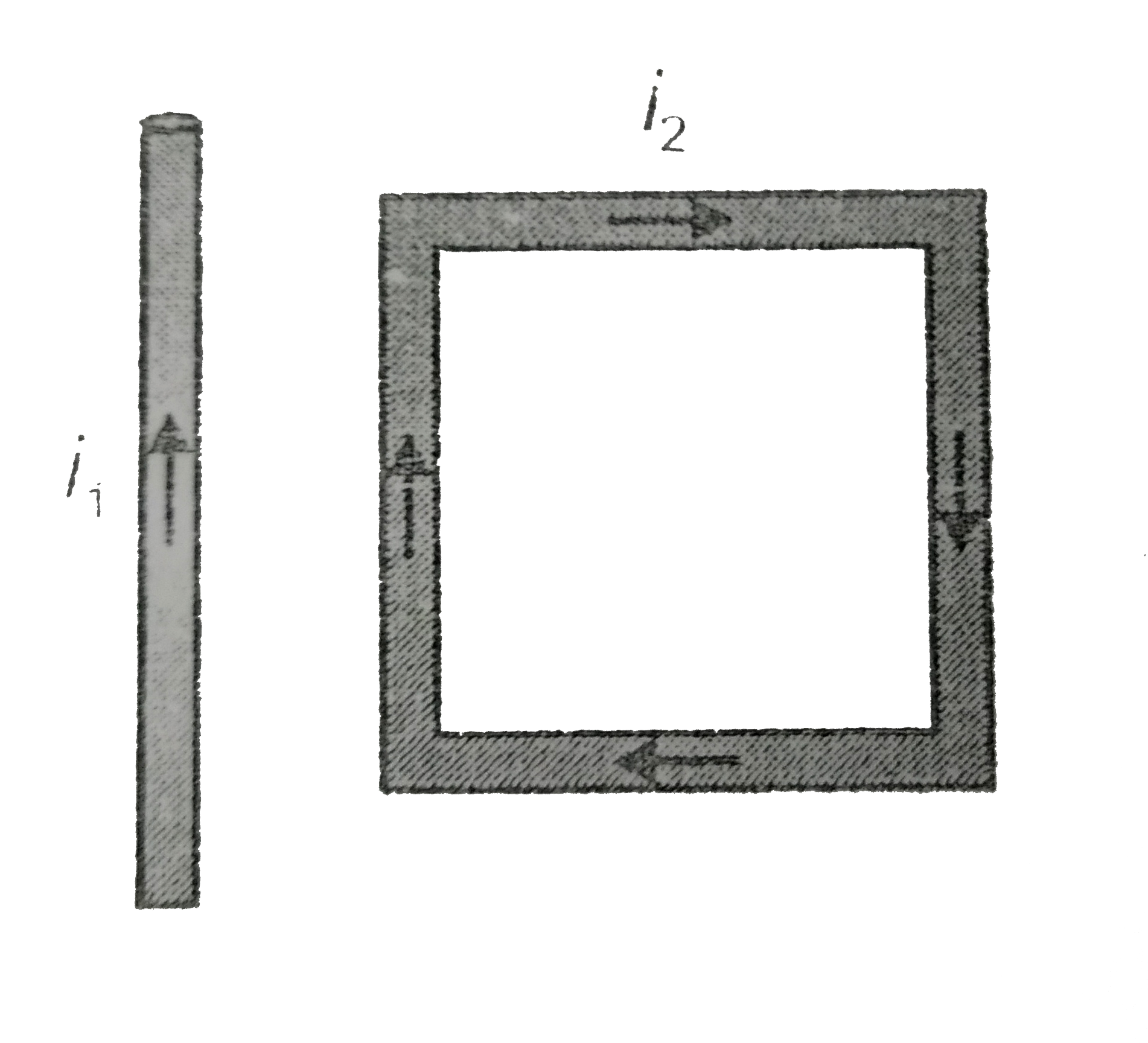
View SolutionA rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
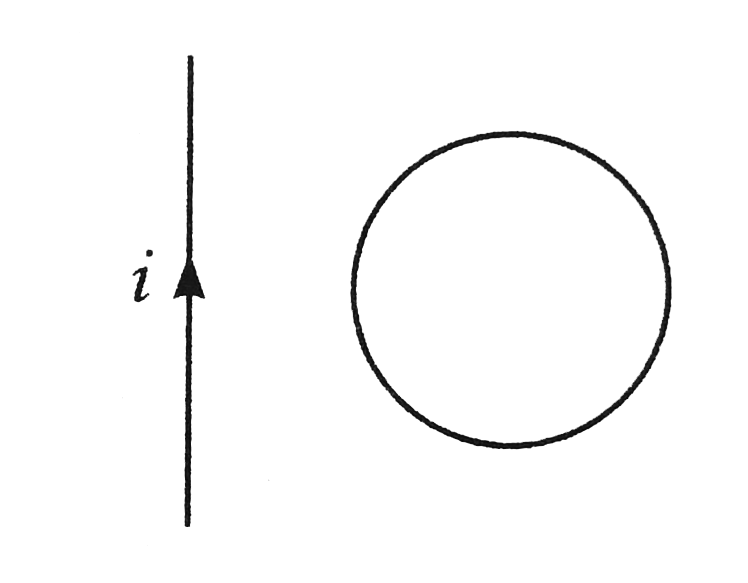
View SolutionFigure shows a conducting loop placed near a long straight wire carrying a current i as shown, if the current increases continuously, find the direction of the induced current in the loop.
View SolutionFigure shows a long straight wire carrying current I and a square conducting wire loop of side l, at a distance 'a' from current wire. Both the current wire and loop are in the plane of paper. Find the flux of magnetic filed of current wire, passing through the loop.

View SolutionShow a conduction loop placed near a long, straight wire carrying current i as shown. If the current increases continuously, find the direction of the induced current in the loop.

View Solution

