A long, straight wire of radius r carries a current i and is placed horizontally in a uniform magnetic field B pointing vertically upward. The current is uniformly distributed over its cross section. (a) At what points will the resultantant magnetic field have maximum magnitude? What will be the maximum magnitude? (b) What will be the minimum magnitude of the resultant magnetic field?
To solve the problem step by step, we will analyze the magnetic field produced by the current in the wire and how it interacts with the external magnetic field.
Step 1: Understand the Setup
We have a long straight wire of radius r carrying a current I. The wire is placed horizontally in a uniform magnetic field B that points vertically upward. The current is uniformly distributed across the wire's cross-section.
Step 2: Magnetic Field Due to the Wire
The magnetic field Bw at a distance x from the center of a long straight wire carrying current I is given by the formula:
Bw=μ0I2πx
where μ0 is the permeability of free space.
Step 3: Determine Maximum Magnetic Field
To find the maximum magnitude of the resultant magnetic field, we need to consider the points where the magnetic field due to the wire and the external magnetic field B combine.
- The magnetic field due to the wire is maximum at the surface of the wire (at a distance r from the center).
- Therefore, at the surface of the wire (where x=r):
Bw=μ0I2πr
- The direction of the magnetic field due to the wire at the surface will be perpendicular to the direction of the external magnetic field B (which is upward).
- The resultant magnetic field at the surface of the wire will be:
Bmax=B+Bw=B+μ0I2πr
Step 4: Determine Minimum Magnetic Field
To find the minimum magnitude of the resultant magnetic field, we consider the center of the wire.
- At the center of the wire, the magnetic field due to the wire is zero:
Bw=0
- Thus, the resultant magnetic field at the center of the wire will only be due to the external magnetic field:
Bmin=B+0=B
Final Answers
(a) The maximum magnitude of the resultant magnetic field occurs at the surface of the wire and is given by:
Bmax=B+μ0I2πr
(b) The minimum magnitude of the resultant magnetic field occurs at the center of the wire and is given by:
Bmin=B
We have a long straight wire of radius r carrying a current I. The wire is placed horizontally in a uniform magnetic field B that points vertically upward. The current is uniformly distributed across the wire's cross-section.
The magnetic field Bw at a distance x from the center of a long straight wire carrying current I is given by the formula:
Bw=μ0I2πx
where μ0 is the permeability of free space.
To find the maximum magnitude of the resultant magnetic field, we need to consider the points where the magnetic field due to the wire and the external magnetic field B combine.
- Therefore, at the surface of the wire (where x=r):
Bw=μ0I2πr
Bmax=B+Bw=B+μ0I2πr
To find the minimum magnitude of the resultant magnetic field, we consider the center of the wire.
Bw=0
Bmin=B+0=B
(a) The maximum magnitude of the resultant magnetic field occurs at the surface of the wire and is given by:
Bmax=B+μ0I2πr
Bmin=B
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:questions for short answer
Explore 12 Videos
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:Objective 2
Explore 7 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective2
Explore 9 Videos
- MAGNETIC PROPERTIES OF MATTERBook:HC VERMA ENGLISHChapter:MAGNETIC PROPERTIES OF MATTERExercise:Short Answer
Explore 6 Videos
Similar Questions
A long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
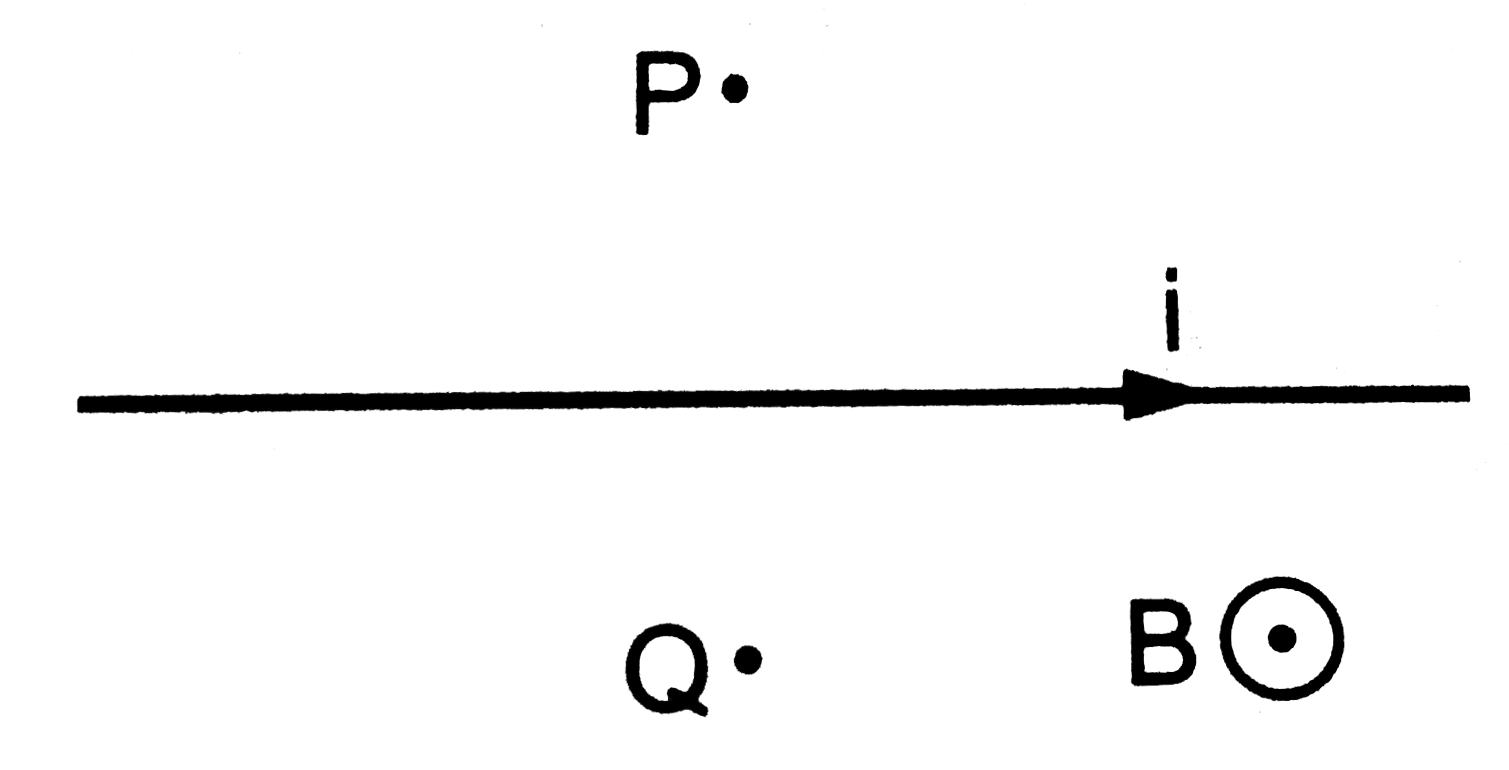
View SolutionA long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B= (1.0×10−5) T pointing vertically upward. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionWhat is the net magnetic field at point O for the current distribution shown here?
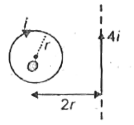
View Solutiona straight wire current element is carrying current 100 A as shown in figure. the magnitude of magnetic field at a point P.

View Solution