A loop of area 1m2 is placed in a magnetic field B=2T, such that plane of the loop is parallel to the magnetic field. If the loop is rotated by 180∘, the amount of net charge passing through any point of loop, it its resistance is 10Ω is
0.4C
0.2C
0.8C
0C
The correct Answer is:A
To solve the problem step by step, we will follow these calculations:
Step 1: Understand the initial conditions
- Area of the loop, A=1m2
- Magnetic field strength, B=2T
- Resistance of the loop, R=10Ω
- The loop is initially parallel to the magnetic field.
Step 2: Calculate the initial magnetic flux
The magnetic flux Φ is given by the formula:
Φ=B⋅A⋅cos(θ)
Where θ is the angle between the magnetic field and the normal to the surface of the loop. Initially, since the plane of the loop is parallel to the magnetic field, θ=0∘.
Thus, the initial flux Φi is:
Φi=B⋅A⋅cos(0∘)=2T⋅1m2⋅1=2Wb
Step 3: Calculate the final magnetic flux after rotation
After rotating the loop by 180∘, the angle θ becomes 180∘. Therefore, the final flux Φf is:
Φf=B⋅A⋅cos(180∘)=2T⋅1m2⋅(−1)=−2Wb
Step 4: Calculate the change in magnetic flux
The change in magnetic flux ΔΦ is given by:
ΔΦ=Φf−Φi=−2Wb−2Wb=−4Wb
However, we are interested in the magnitude of the change:
|ΔΦ|=4Wb
Step 5: Calculate the induced EMF using Faraday's Law
According to Faraday's Law of Electromagnetic Induction, the induced EMF E is equal to the rate of change of magnetic flux:
E=−ΔΦΔt
Since we are not given a specific time interval Δt, we will use the total change in flux for the calculation of charge.
Step 6: Calculate the induced current
Using Ohm's Law, the induced current I can be calculated as:
I=ER
Substituting the induced EMF:
I=|ΔΦ|R=4Wb10Ω=0.4A
Step 7: Calculate the total charge passing through the loop
The total charge Q that passes through the loop can be calculated using the formula:
Q=I⋅t
If we assume that the time t during which the flux changes is 1 second (for simplicity), then:
Q=0.4A⋅1s=0.4C
Final Answer
The amount of net charge passing through any point of the loop is 0.4C.
---
- Area of the loop, A=1m2
- Magnetic field strength, B=2T
- Resistance of the loop, R=10Ω
- The loop is initially parallel to the magnetic field.
The magnetic flux Φ is given by the formula:
Φ=B⋅A⋅cos(θ)
Where θ is the angle between the magnetic field and the normal to the surface of the loop. Initially, since the plane of the loop is parallel to the magnetic field, θ=0∘.
Φi=B⋅A⋅cos(0∘)=2T⋅1m2⋅1=2Wb
After rotating the loop by 180∘, the angle θ becomes 180∘. Therefore, the final flux Φf is:
Φf=B⋅A⋅cos(180∘)=2T⋅1m2⋅(−1)=−2Wb
The change in magnetic flux ΔΦ is given by:
ΔΦ=Φf−Φi=−2Wb−2Wb=−4Wb
However, we are interested in the magnitude of the change:
|ΔΦ|=4Wb
According to Faraday's Law of Electromagnetic Induction, the induced EMF E is equal to the rate of change of magnetic flux:
E=−ΔΦΔt
Since we are not given a specific time interval Δt, we will use the total change in flux for the calculation of charge.
Using Ohm's Law, the induced current I can be calculated as:
I=ER
Substituting the induced EMF:
I=|ΔΦ|R=4Wb10Ω=0.4A
The total charge Q that passes through the loop can be calculated using the formula:
Q=I⋅t
If we assume that the time t during which the flux changes is 1 second (for simplicity), then:
Q=0.4A⋅1s=0.4C
The amount of net charge passing through any point of the loop is 0.4C.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA current loop placed in a magnetic field behaves like a
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
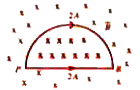
View SolutionA metallic loop is placed in a magnetic field. If a current is passed through it, then
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m

View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m

View SolutionAssertion A conducting loop is rotated in a uniform magnetic field with constant angular velocity ω as shown in figure. At time t = 0, plane of the loop is perpendicular to the magnetic field. Induced emf produced in the loop is maximum when plane of loop is parallel to magnetic field.
Reason When plane of loop is parallel to magnetic field, then magnetic flux passing through the loop is zero.
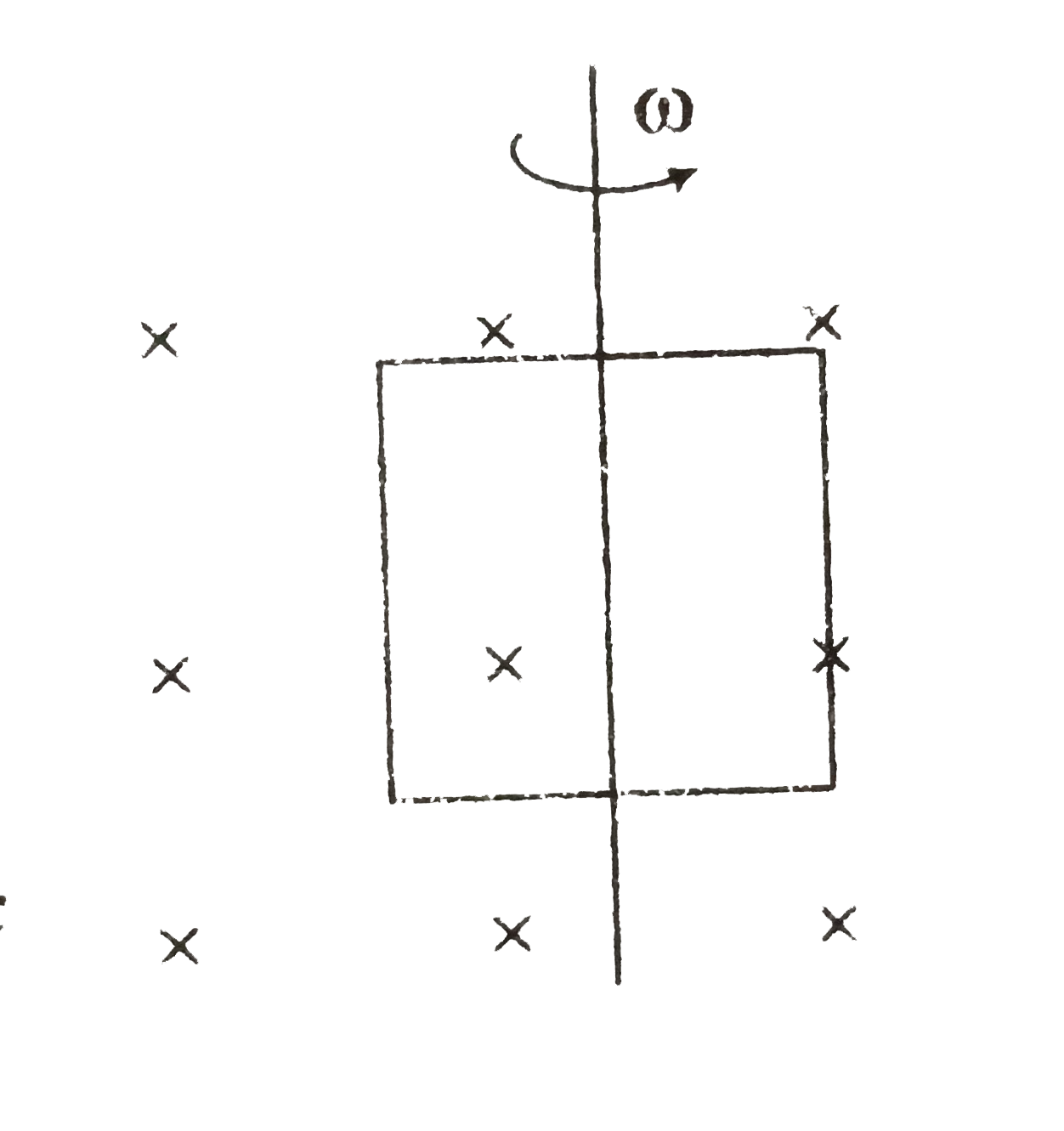
View SolutionA circular loop of area 1cm2 , carrying a current of 10 A , is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
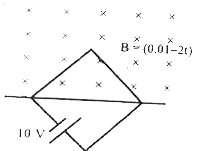
View SolutionA square loop of side 1 m is placed in a perpendicular magnetic field. Half of the area of the loop lies inside the magnetic field . A battery of emf 10 V and negligible intermal resistance is connected in the loop . The magnetic field changes with time according to the relation B= (0.01 -2t) tesla . The resultant emf of the circuit is
View Solution
