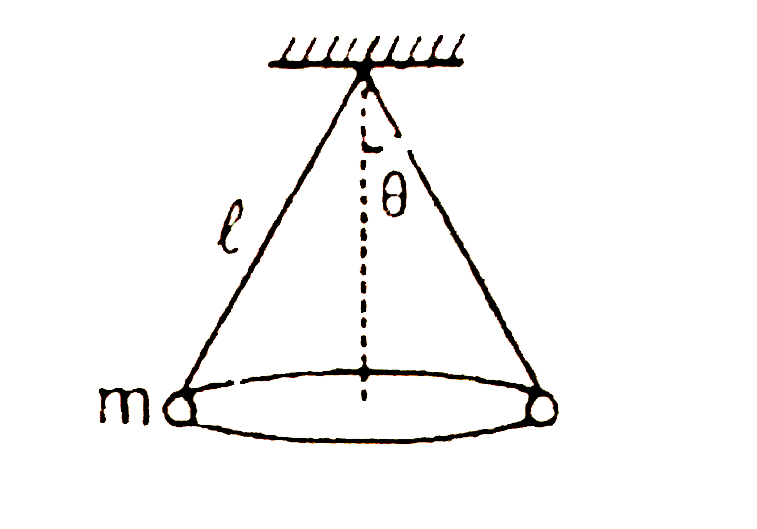
A mass is suspended from the ceiling by a string revolving in a horizontal circle of radius 5 cm. The tangential speed of the mass is 0.7 m $\cdot s^{- 1}$ . What is the angle between the string and the vertical? (Consider acceleration due to gravity as 9.8 m $\cdot s^{- 2}$ )

Text Solution

Verified by Experts

Let the angle between the string and the vertical be $θ$ .
tan $θ = \frac{\frac{m v^{2}}{r}}{m g} = \frac{v^{2}}{r g}$
Here, r = 5 cm = 0.05 m,
v = 0.7 m $\cdot s^{- 1}$ , g = 9.8 m $\cdot s^{- 2}$
So, tan $θ = \frac{{(0.7)}^{2}}{0.05 \times 9.8}$ = 1 or, $θ = 45^{\circ}$ .

Updated on:21/07/2023

A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
A $\frac{r g}{\sqrt{L^{2} - r^{2}}}$
B $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$
C $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
D $\frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
A body of mass 1 kg tied to one end of string is revolved in a horizontal circle of radius 0.1 m with a speed of $3 revolution / sec$ , assuming the effect of gravity is negligible, then linear velocity, acceleration and tension in the string will be
A $1.88 m / s, 35.5 m / s^{2}, 35.5 N$
B $2.88 m / s, 45.5 m / s^{2}, 45.5 N$
C $3.88 m / s, 55.5 m / s^{2}, 55.5 N$
DNone of these
A car is moving along a horizontal curve of radius 20 m , and coefficient of friction between the road and wheels of the car is $0.25$ . If acceleration due to gravity is $(9.8 m / s^{2})$ , then its maximum speed is
A $3 m / s$
B $5 m / s$
C $7 m / s$
D $9 m / s$