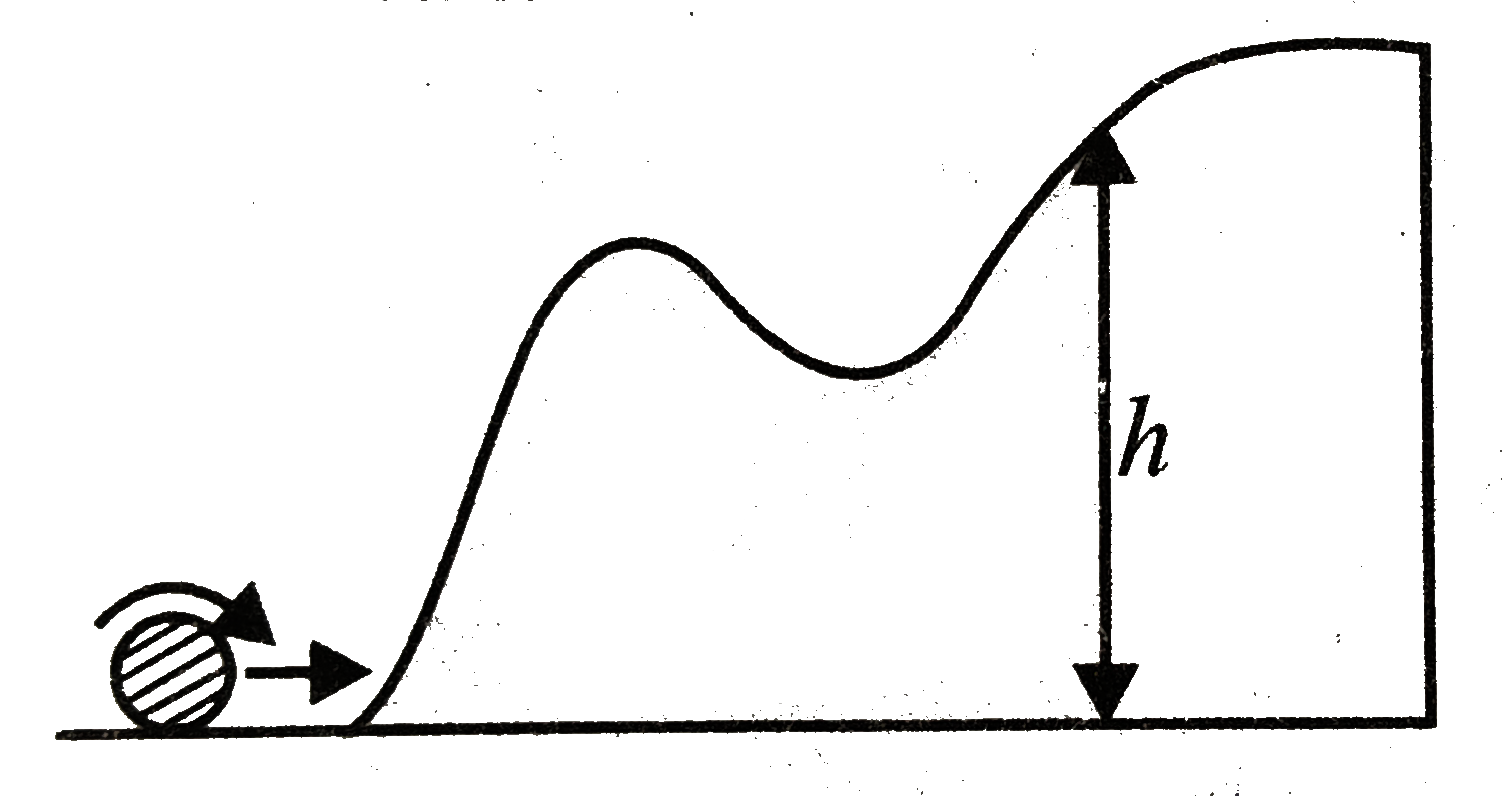
A mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
the body is identified to be a disc or a solid cylinder
the body is a solid sphere
moment of inertia of the body about instantaneous axis of rotation is 32mr2
moment of inertial of the body about instantaneous axis of rotation is 75mr2
To solve the problem of a mass m rolling without slipping and reaching a height of 34v2g, we can follow these steps:
Step 1: Understand the Energy Conservation Principle
When the mass rolls up to a height, its kinetic energy is converted into potential energy. The total mechanical energy is conserved since there is no external work done (assuming no friction losses).
Step 2: Write the Initial Kinetic Energy
The total kinetic energy KE of a rolling object consists of translational and rotational kinetic energy:
KE=KEtrans+KErot=12mv2+12Iω2
where I is the moment of inertia and ω is the angular velocity.
Step 3: Relate Angular Velocity to Linear Velocity
For rolling without slipping, the relationship between linear velocity v and angular velocity ω is given by:
ω=vr
Substituting this into the kinetic energy equation gives:
KE=12mv2+12I(vr)2
Step 4: Substitute Moment of Inertia
Assuming the object is a solid sphere, the moment of inertia I about its center of mass is:
I=25mr2
Substituting this into the kinetic energy equation:
KE=12mv2+12(25mr2)(v2r2)
This simplifies to:
KE=12mv2+15mv2=710mv2
Step 5: Write the Potential Energy at Height h
The potential energy PE at height h is given by:
PE=mgh
Substituting the given height h=34v2g:
PE=mg(34v2g)=34mv2
Step 6: Set Kinetic Energy Equal to Potential Energy
Using conservation of energy:
KE=PE
Substituting the expressions we derived:
710mv2=34mv2
Step 7: Solve for the Height
To find the height, we can rearrange the equation:
710mv2=34mv2
This shows that the initial kinetic energy is indeed converted to potential energy at the height given in the problem.
Conclusion
The mass rolls up to a height of 34v2g as stated in the problem.
---
When the mass rolls up to a height, its kinetic energy is converted into potential energy. The total mechanical energy is conserved since there is no external work done (assuming no friction losses).
The total kinetic energy KE of a rolling object consists of translational and rotational kinetic energy:
KE=KEtrans+KErot=12mv2+12Iω2
where I is the moment of inertia and ω is the angular velocity.
For rolling without slipping, the relationship between linear velocity v and angular velocity ω is given by:
ω=vr
Substituting this into the kinetic energy equation gives:
KE=12mv2+12I(vr)2
Assuming the object is a solid sphere, the moment of inertia I about its center of mass is:
I=25mr2
Substituting this into the kinetic energy equation:
KE=12mv2+12(25mr2)(v2r2)
This simplifies to:
KE=12mv2+15mv2=710mv2
The potential energy PE at height h is given by:
PE=mgh
Substituting the given height h=34v2g:
PE=mg(34v2g)=34mv2
Using conservation of energy:
KE=PE
Substituting the expressions we derived:
710mv2=34mv2
To find the height, we can rearrange the equation:
710mv2=34mv2
This shows that the initial kinetic energy is indeed converted to potential energy at the height given in the problem.
The mass rolls up to a height of 34v2g as stated in the problem.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
View SolutionA body of radius R and mass m is rolling smoothly with speed v on a horizontal surface. It then rolls up a hill to a maximum height h. If h=3v2/4g. What might the body be ?
View SolutionA body of mass M and radius r, rolling on a smooth horizontal floor with velocity v, rolls up an irregular inclined plane up to a vertical height (3v2/4g). Compute the moment of inertia of the body.
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionA uniform disc of mass m and radius R is thrown on horizontal lawn in such a way that it initially slides with speed V0 without rolling. The distance travelled by the disc till it starts pure rolling is (Coefficient friction between the contact is 0.5)
View SolutionA small sphere of mass 1 kg is rolling without slipping with linear speed
v=√2007m/s

It leaves the inclined plane at point C.
Find the linear speed at point C.
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View SolutionA disc rolls over a horizontal floor without slipping with a linear speed of 5 cm/sec. Then the linear speed of a particle on its rim, with respect to the floor, when it is in its highest position is?
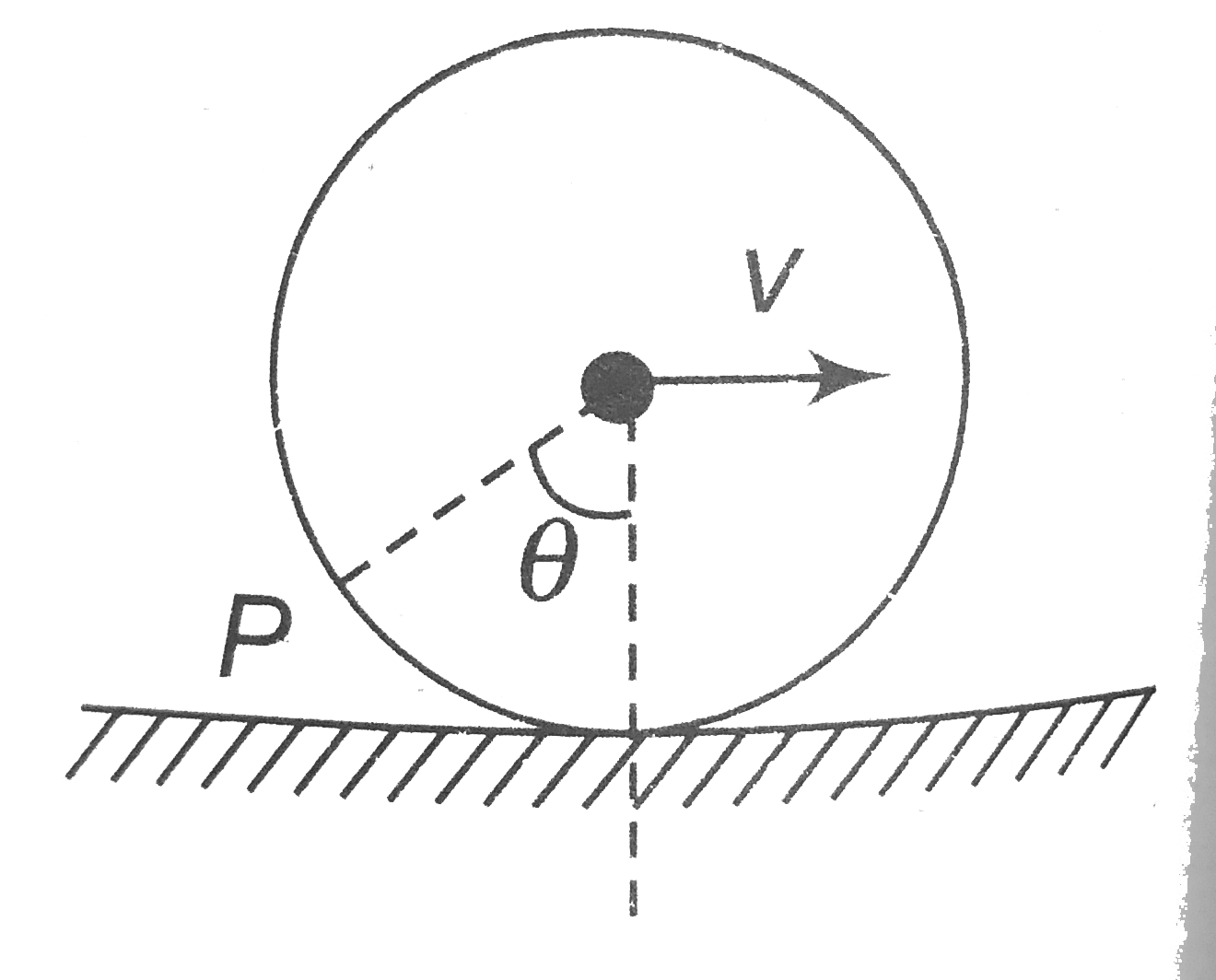
View SolutionA hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
View Solution
