A disc rolls over a horizontal floor without slipping with a linear speed of 5 cm/sec. Then the linear speed of a particle on its rim, with respect to the floor, when it is in its highest position is?
10cm/sec
5cm/sec
2.5cm/sec
0
The correct Answer is:A
To solve the problem, we need to determine the linear speed of a particle on the rim of a disc when it is at its highest position, given that the disc rolls without slipping with a linear speed of 5 cm/sec.
1. Understand the Motion of the Disc:
- The disc rolls on a horizontal surface without slipping. This means that the point of contact with the ground (let's call it point A) is momentarily at rest.
2. Identify the Linear Speed:
- The linear speed (V) of the center of the disc is given as 5 cm/sec.
3. Relate Linear Speed to Angular Speed:
- For a disc rolling without slipping, the relationship between linear speed (V) and angular speed (ω) is given by:
V=ωR
- Here, R is the radius of the disc.
4. Determine the Speed at the Highest Point:
- The highest point of the disc (let's call it point C) will have two components of velocity:
- The linear speed of the center of the disc (V) acting forward.
- The tangential speed due to rotation (ωR), which is also acting forward at the highest point.
- Since the disc rolls without slipping, at the highest point, the total speed (V_C) can be expressed as:
VC=V+ωR
- Since V=ωR, we can substitute this into the equation:
VC=V+V=2V
5. Calculate the Speed at the Highest Point:
- Now substituting the value of V:
VC=2×5 cm/sec=10 cm/sec
6. Conclusion:
- The linear speed of the particle on the rim at its highest position with respect to the floor is 10 cm/sec.
- The disc rolls on a horizontal surface without slipping. This means that the point of contact with the ground (let's call it point A) is momentarily at rest.
- The linear speed (V) of the center of the disc is given as 5 cm/sec.
- For a disc rolling without slipping, the relationship between linear speed (V) and angular speed (ω) is given by:
V=ωR
- Here, R is the radius of the disc.
- The highest point of the disc (let's call it point C) will have two components of velocity:
- The linear speed of the center of the disc (V) acting forward.
- The tangential speed due to rotation (ωR), which is also acting forward at the highest point.
- Since the disc rolls without slipping, at the highest point, the total speed (V_C) can be expressed as:
VC=V+ωR
- Since V=ωR, we can substitute this into the equation:
VC=V+V=2V
- Now substituting the value of V:
VC=2×5 cm/sec=10 cm/sec
- The linear speed of the particle on the rim at its highest position with respect to the floor is 10 cm/sec.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-14videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-25videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE56videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
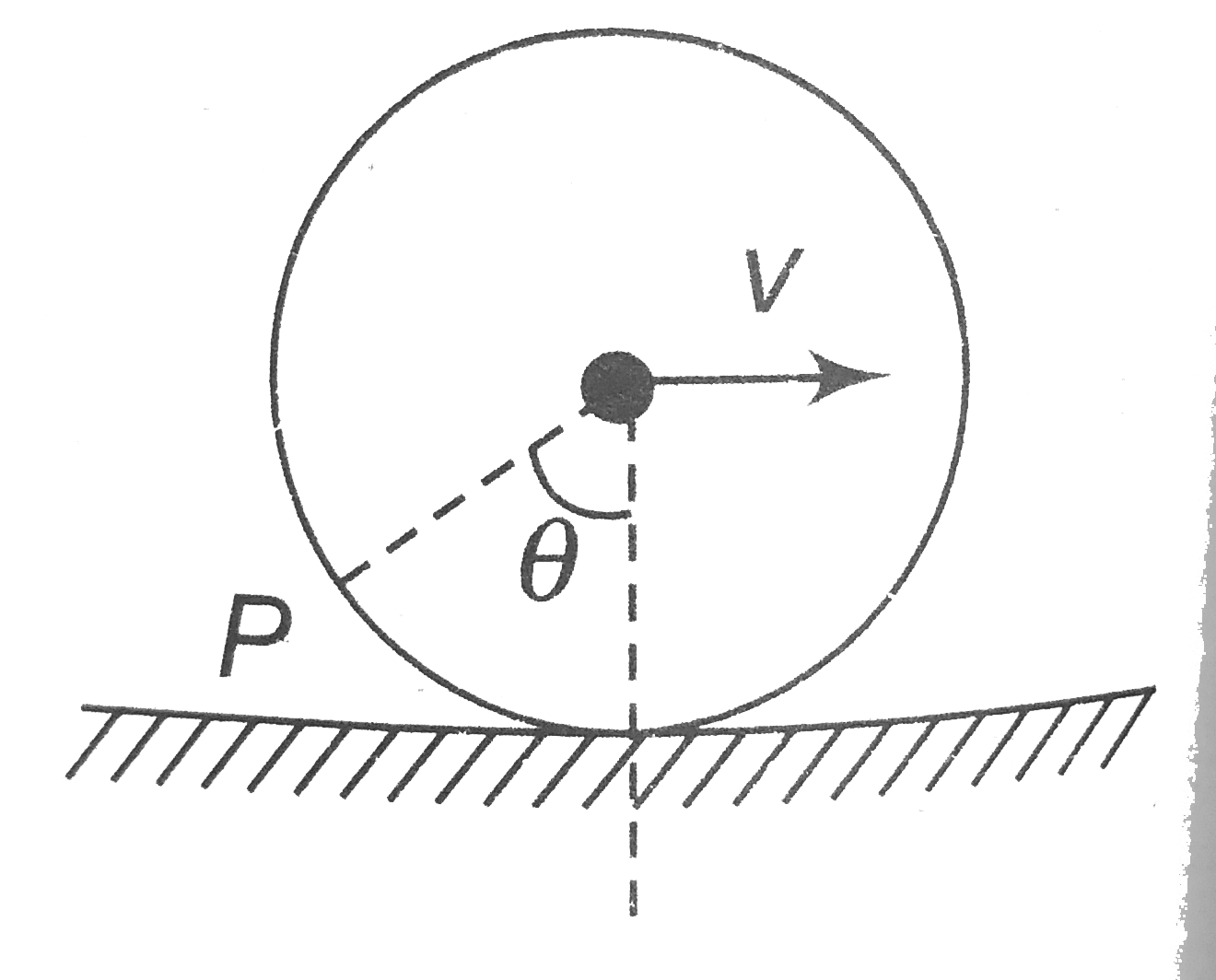
A hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
 View Solution
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionA disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of the radius.View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionIf the speed of a particle moving at a relativistic speed is doubled, its linear momentum will
View SolutionA mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
View SolutionA hollow sphere rolls without slipping down a plane inclined at an angle of 30° to the horizontal. Its linear acceleration will be
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View SolutionA small sphere of mass 1 kg is rolling without slipping with linear speed
v=√2007m/s

It leaves the inclined plane at point C.
Find the linear speed at point C.View Solution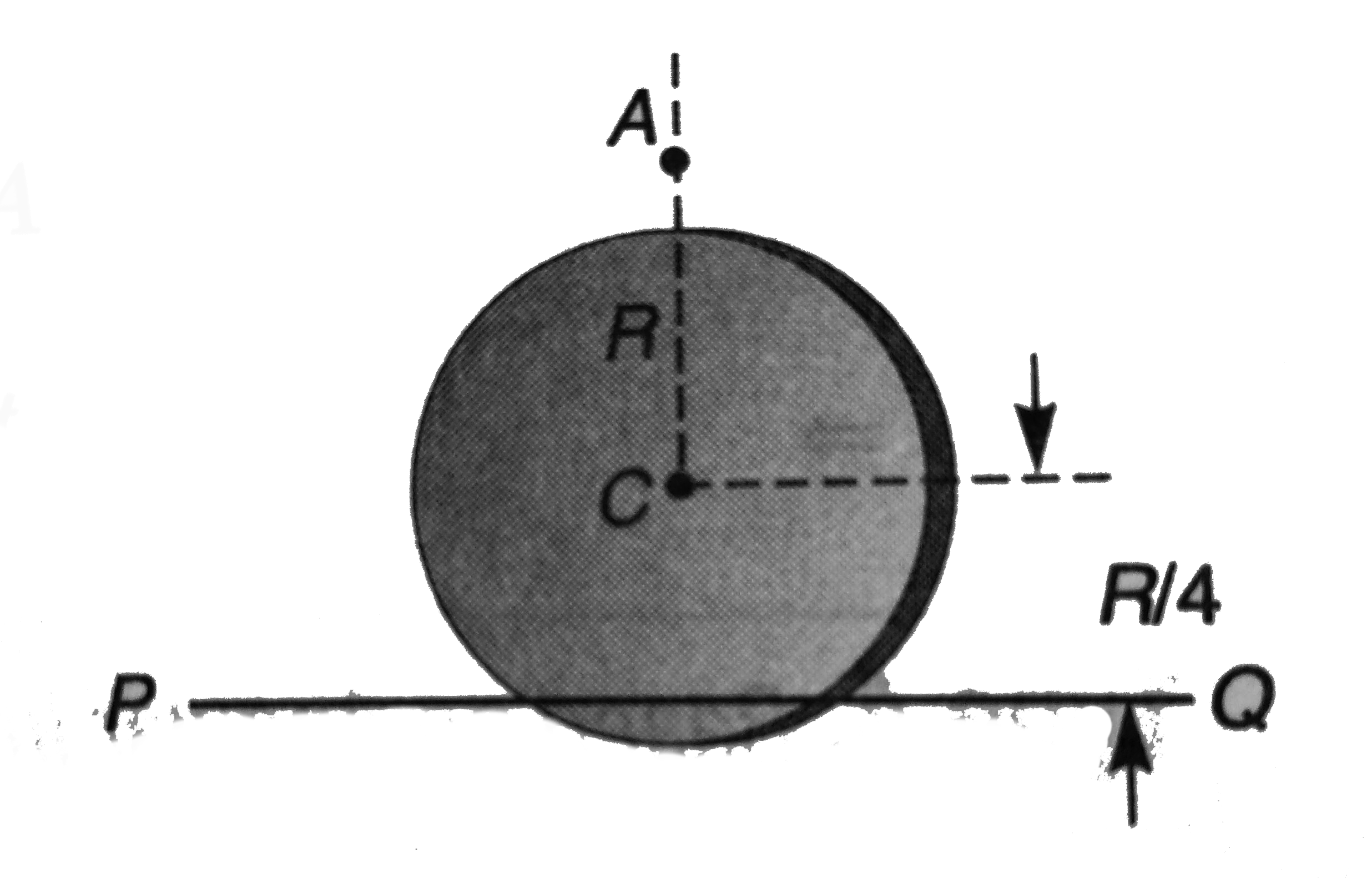
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.View Solution

