A metal disc of radius R can rotate about the vertical axis passing through its centre. The top surface of the disc is uniformly covered with dust particles. The disc is rotated with gradually increasing speed. At what value of the angular speed (ω) of the disc the 75%of the top surface will become dust free. Assume that the coefficient of friction between the dust particles and the metal disc is μ=0.5. Assume no interaction amongst the dust particles.
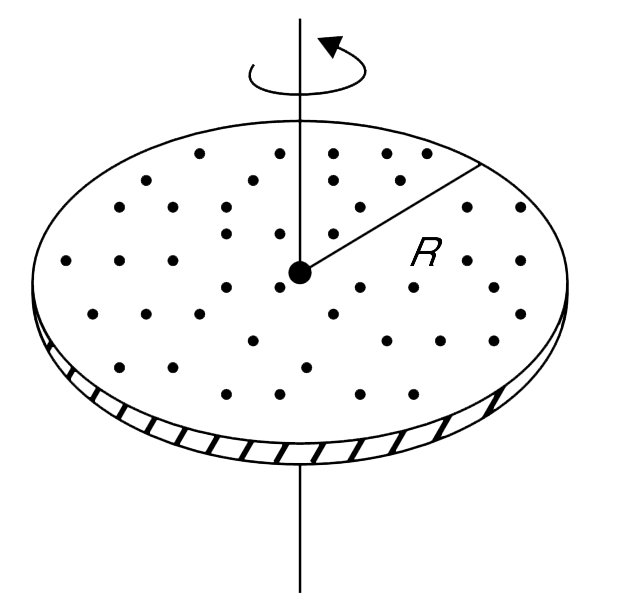
The correct Answer is:ω=√gR
Step by step video, text & image solution for A metal disc of radius R can rotate about the vertical axis passing through its centre. The top surface of the disc is uniformly covered with dust particles. The disc is rotated with gradually increasing speed. At what value of the angular speed (omega) of the disc the 75% of the top surface will become dust free. Assume that the coefficient of friction between the dust particles and the metal disc is mu = 0.5. Assume no interaction amongst the dust particles. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle is acted upon by a force for 1 second whose X component remains constant at Fx=30N but y and z components vary with time as shown in the graph. Calculate the magnitude of change in momentum of the particle in 1 s. What angle does the change in momentum (Δ→P) make with X axis ?

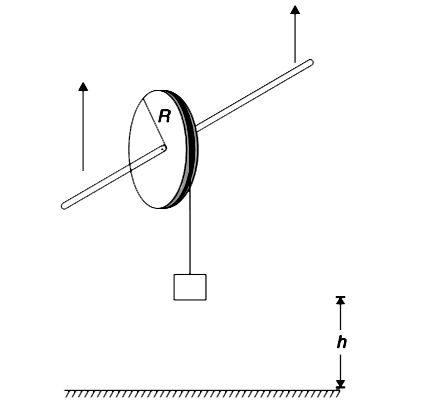
View SolutionThe pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionA uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis, passing through the centre of the disc. A piece of disc from its rim detaches itself from the disc at the instant when it is, on the same horizontal with the centre of the disc and moving upwards. lien about the fixed axis, the angular speed of the
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same angular velocity mass m and moving horizontally with velocity 2omegaR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
View SolutionA circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
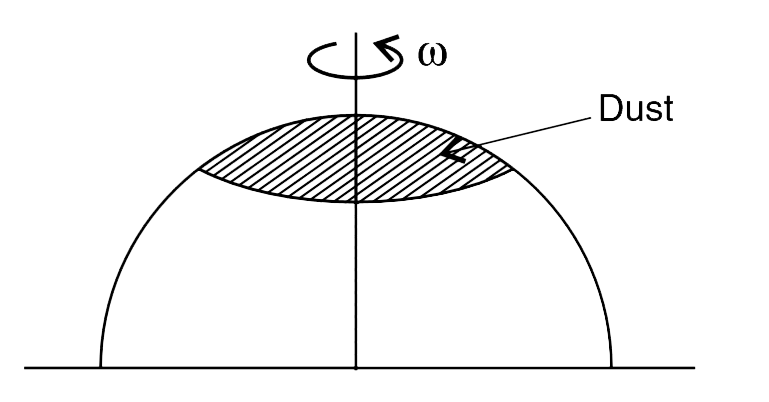
View SolutionA metallic hemisphere is having dust on its surface. The sphere is rotated about a vertical axis passing through its centre at angular speed ω=10rads–1. Now the dust is visible only on top 20% area of the curved hemispherical surface. Radius of the hemisphere is R = 0.1 m. Find the coefficient of friction between the dust particle and the hemisphere [g=10ms–2].
View SolutionA thin metallic disc is rotating with constant angular velocity about a vertical axis that is perpendicular to its plane and passes through its centre. The rotation causes the free electrons in the disc to redistribute. Assume that there is no external electric or magnetic field. Then
View SolutionA flat disc of radius R charged uniformly on its surface at a surface charge density sigma . About its central axis of rotation it rotates at an angular speed omega . Find the magnetic moment of disc due to rotation of charges.
View SolutionA uniform disc is rotating at a constantt speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upward. Then about the fixed axis, the angular speed of the
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA disc is free to rotate about a smooth horizontal axis passing through its centre of mass. A particle is fixed at the top of the disc. A slight push is given to the disc and it starts rotating. During the process.

View SolutionAn uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upwards, then about the fixed axis.
STATEMENT-1 : Angular speed of the disc about the aixs of rotation will increase.
and
STATEMENT-2 : Moment of inertia of the disc is decreased about the axis of rotation.
View SolutionAssertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v. Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R . It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution
