Question

A metal rod of length 'L' and mass 'm' is pivoted at one end. A thin disk of mass 'M' and radius 'R' (< L) is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A) - The disc is not free to rotate about its centre and (case B) - the disc is free to rotate about its centre. The rod-disc system after being released from the same displaced position. Which of the following statement(s) is(are) true?

Options

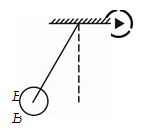
A. (a)Restoring torque in case `A` = Resorting torque in case `B`
B. (b)Restoring torque in case `A` lt Restoring torque in case `B`
C. (c)Angular frequency for case `A` gt Angular frequency for case `B`
D. (d)Angular frequency for case `A` lt Angular frequency for case `B`.

Answer

A::D

Explanation

Torque is same for both the cases.
`T=2pi sqrt((I)/((M+m)gd))`
`I_(A) =(mL^(2))/(3) +((MR^(2))/(2)+ ML^(2))`
When the disc is free to rotate about its centre, it will not rotate w.r.t. ground. It will act as a point mass, so moment of inertia is given by
`I_(B)=(mL^(2))/(3)+ ML^(2)`
`I_(A) gt I_(B) rArr T_(A) gt T_(B) rArr omega_(A) lt omega_(B)`.