A metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R'(<L). Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
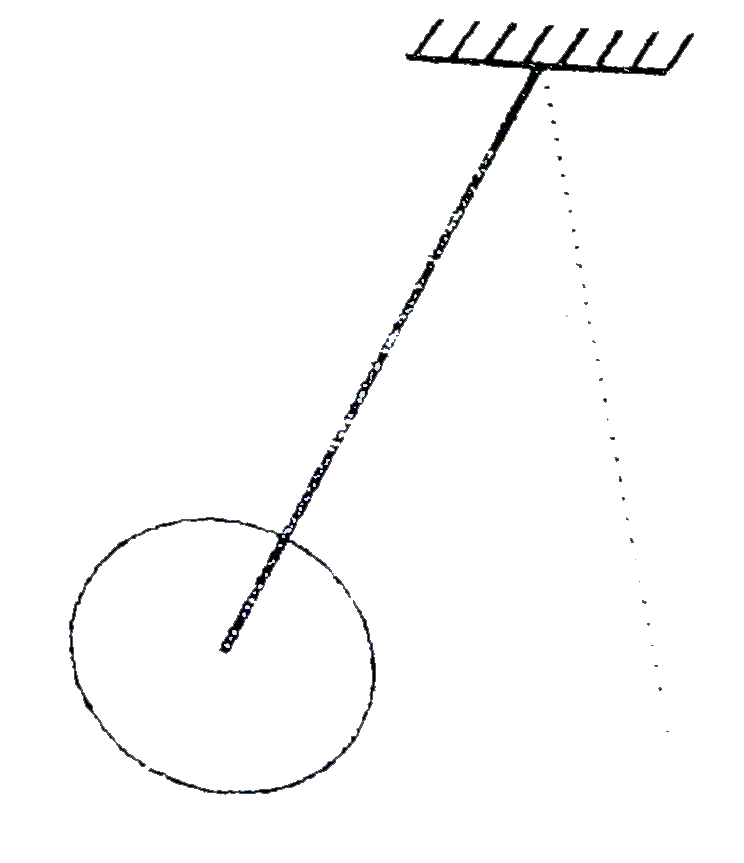
Restoring torque in case A = Restoring torque in case B
Restoring torque in case A lt Restoring torque in case B
Angular frequency for case A gt Angular frequency for case B
Angular frequency for case A lt Angular frequency for case B
The correct Answer is:AD
Torque is same both the cases.
T=2π√I(M+m)gd (Where d is the distance of C.M from pivot)
IA=mL23+(MR22+ML2)
When the disc is free to rotate about its centre, it will not rotate w.r.t. ground. It will act as a point mass, so moment of inertia is given by
IE=mL23+ML2 because IA>IB⇒TA>TB⇒ωA<ωB
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 6-previous year question
56 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
Similar Questions
A metal rod of length 'L' and mass 'm' is pivoted at one end. A thin disk of mass 'M' and radius 'R' (< L) is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A) - The disc is not free to rotate about its centre and (case B) - the disc is free to rotate about its centre. The rod-disc system after being released from the same displaced position. Which of the following statement(s) is(are) true?
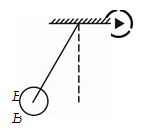
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View Solution
Knowledge Check
Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
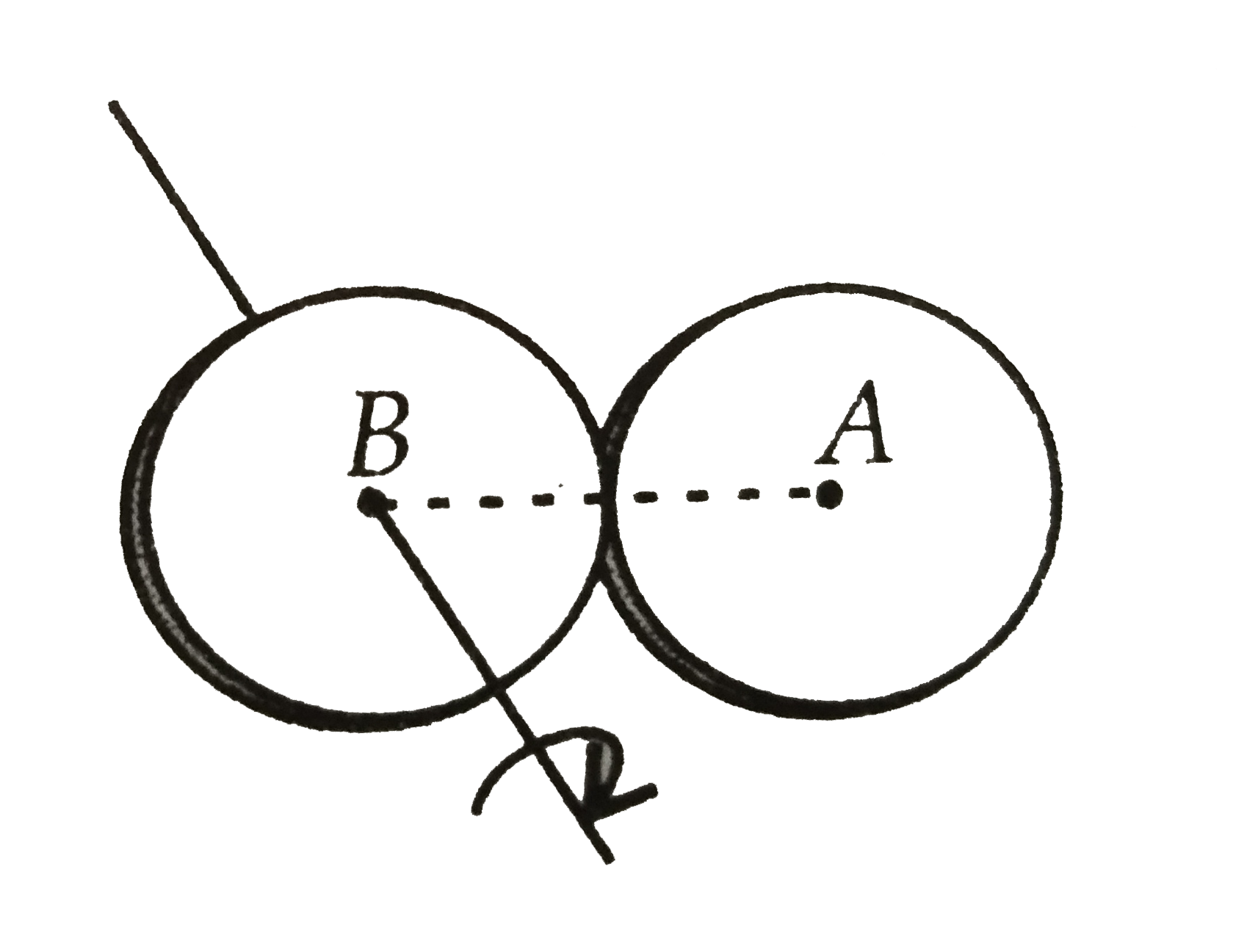 A2Mr2B3Mr2C4Mr2D5Mr2
A2Mr2B3Mr2C4Mr2D5Mr2
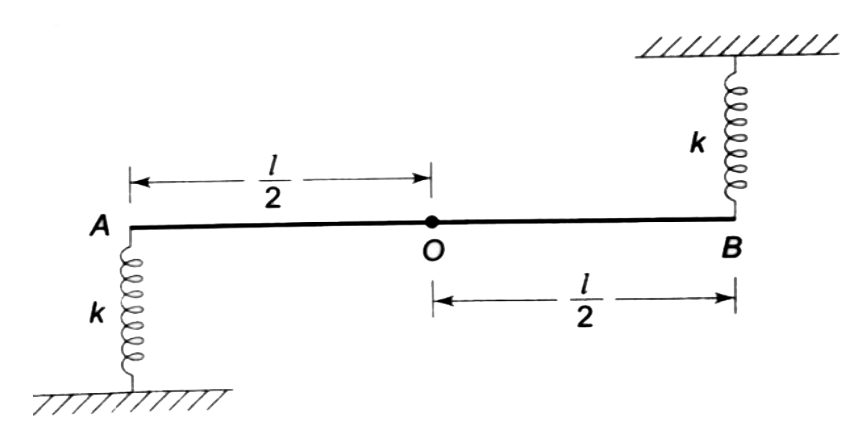
The ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
View SolutionA disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
View SolutionThe moment of inertia of a disc of mass M and radius R about an axis. Which is tangential to sircumference of disc and parallel to its diameter is.
View SolutionTwo equal and opposite forces F are allplied tangentially to a uniform disc of mass M and radius R . If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :
View SolutionFind the moment of inertia A of a spherical ball of mass m and radius r attached at the end of a straight rod of mass M and length l, if this system is free to rotate about an axis passing through the end of the rod (end of the rod opposite to sphere).

View SolutionThe thin rod shown below has mases M and length L. A force F acts at one end as shown and the rod is free to rotate about the other end in horizontal plane. Initial angular acceleration of the rod is :

View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-

View Solution
