A non-conducting ring of mass m and radius R is charged as shown. The charge density, i.e. charge per unit length is . It is then placed on a rough non-conducting horizontal plane. At time , a uniform electric field is switched on and the ring starts rolling without sliding. Determine the friction force (magnitude and direction) acting on the ring when it starts moving.
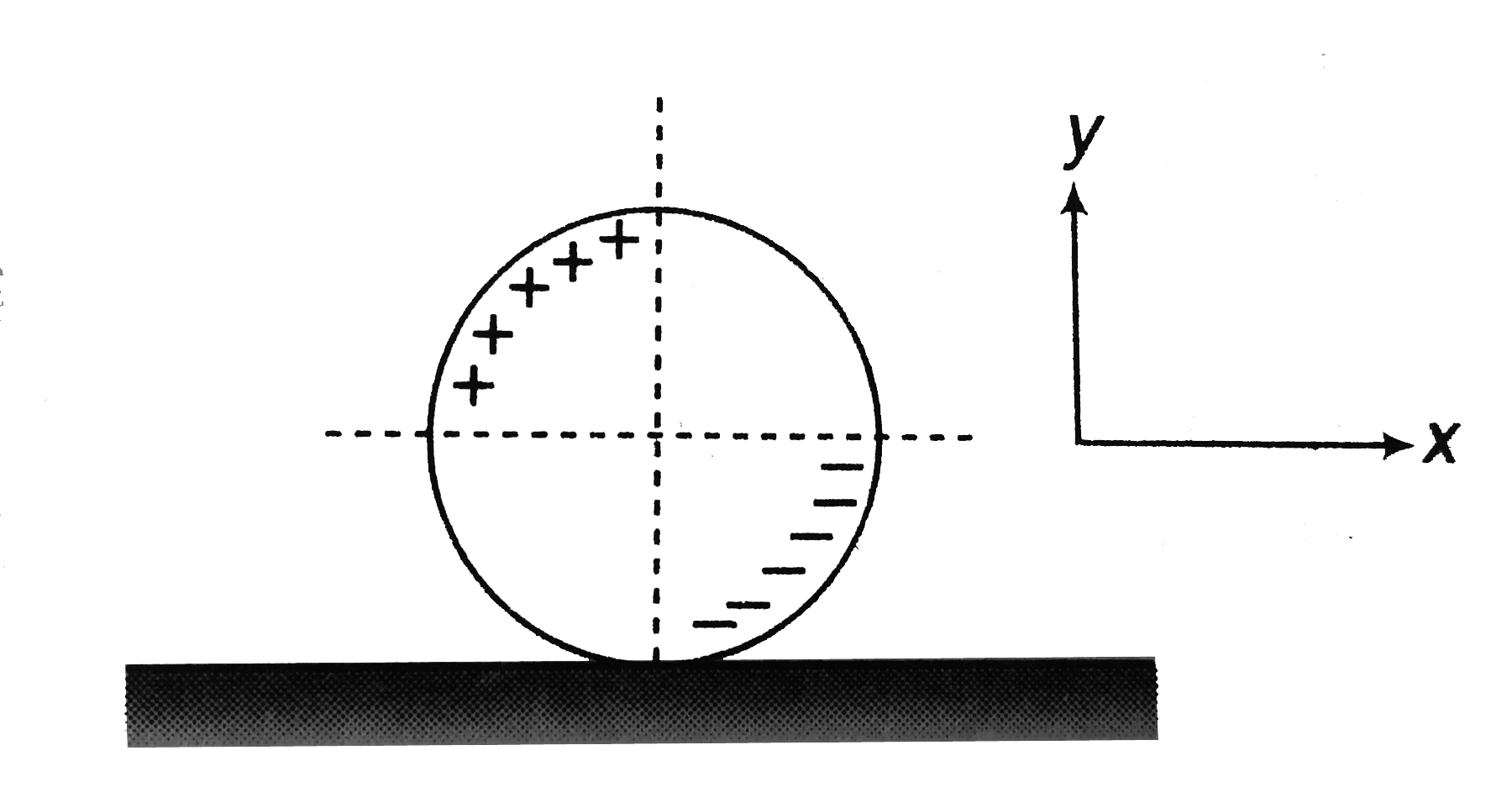
Consider a differential element subtending an angle at the center and at an angel as shown in fig.
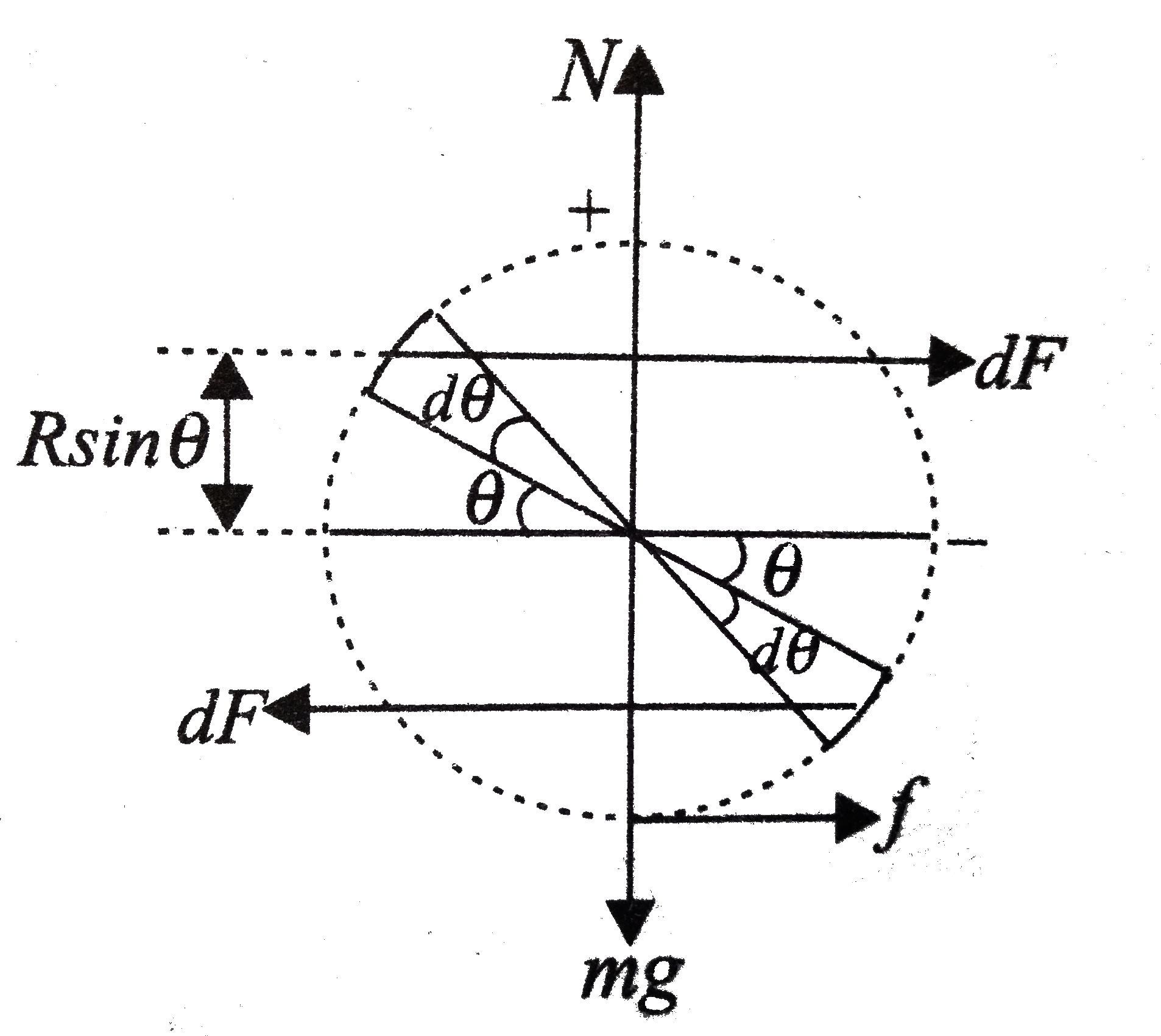
Net torque due to electric field is
Torque due to electric charges is
Torque equation is
or
...(i)
Force equation ...(ii)
For rolling ...(iii)
Solving eqs,(i),(ii), and (iii), we get
along the positive x-axis.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
A nonconducting ring of mass m and radius R, with charge per unit length λ is shown in fig. It is then placed on a rough nonconducting horizontal plane. At time t=0, a uniform electric field →E=E0ˆi is switched on and the ring starts rolling without sliding. Determine the friction force (magnitude and direction ) acting on the ring.

View SolutionA non conducting solid sphere of mass m and radius R having uniform charge density +ρ and −ρ as shown in figure. It is then placed on a rough non conducting horizontal plane. At t=0 a uniform electric field →E=E0ˆiN/C is switched on and the solid sphere starts rolling with sliding. The magnitude of frictional force at t=0 is 2ρπR3E0K. Find the value of K

View SolutionA non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B=B0t2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre.
(a) Find friction coefficient μ between the ring and the surface.
(b) If magnetic field is switched off after 4s, then find the angle rotated by the ring before coming to stop after switching off the magnetic field.
View SolutionA uniform nonconducting rod of mass ma and length l, with charge density λ as shown in fig. is hanged at the midpoint at origin so that it can rotate in a horizontal plane without any friction. A uniform electric field E exists parallel to x axis in the entire region. Calculated the period of small oscillation of the rod .

View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t3T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be k24. Then the value of k is
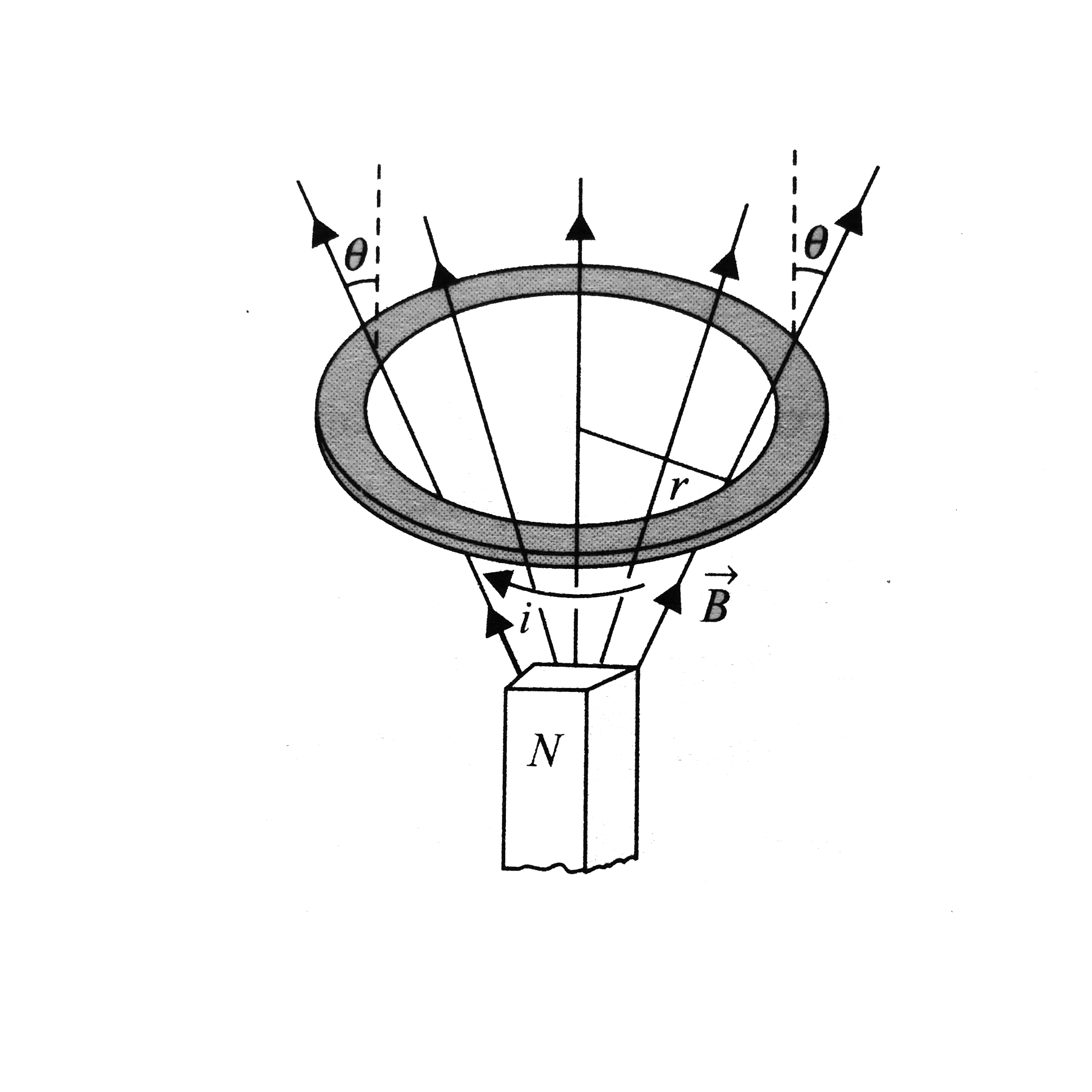
View SolutionA strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle θ with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?
View SolutionA non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field B=4t2 is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
View SolutionA non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field B=4t2 is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionA uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v0 and angular ω0=2v0R and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction μ=2tanθ as shown. The time after which the sphere will start rolling without slipping is

View Solution
