A nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane.
We know ∮E.ds=qε0
E.x.d=(ρ(x2)dε0),E=(ρxε0) .
Topper's Solved these Questions
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 2
8 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
Similar Questions
A ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionA long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
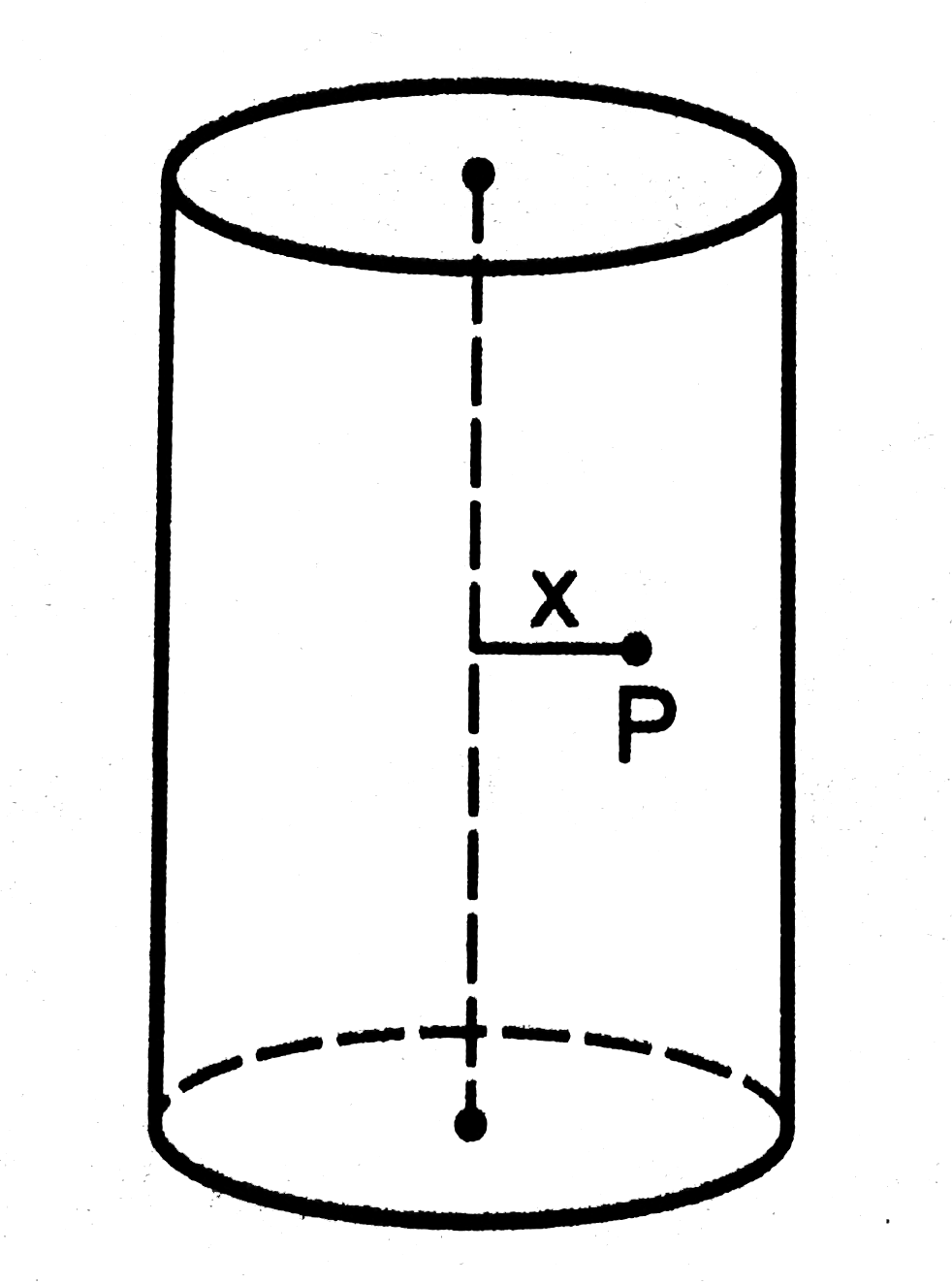
View Solution
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
A spherical volume contains a uniformaly distributed charge of density 2.0×10−4Cm3. Find the electric field at a piont inside the volume at a distance 4.0 cm from the centre.
View Solution
An infinite non-conducting plate of charge has thickness d and contains uniform charge distribution fo charge density, which one of the following graphs represents the variation of electric field E(x) with x. (here x is the distance from central plane of non-conducting plate)
View SolutionAn infinitely large non-conducting plane of uniform surface charge density σ has circular aperture of certain radius carved out from it. The electric field at a point which is at a distance 'a' from the centre of the aperture (perpendicular to the plane) is σ2√2∈0. Find the radius of aperture :
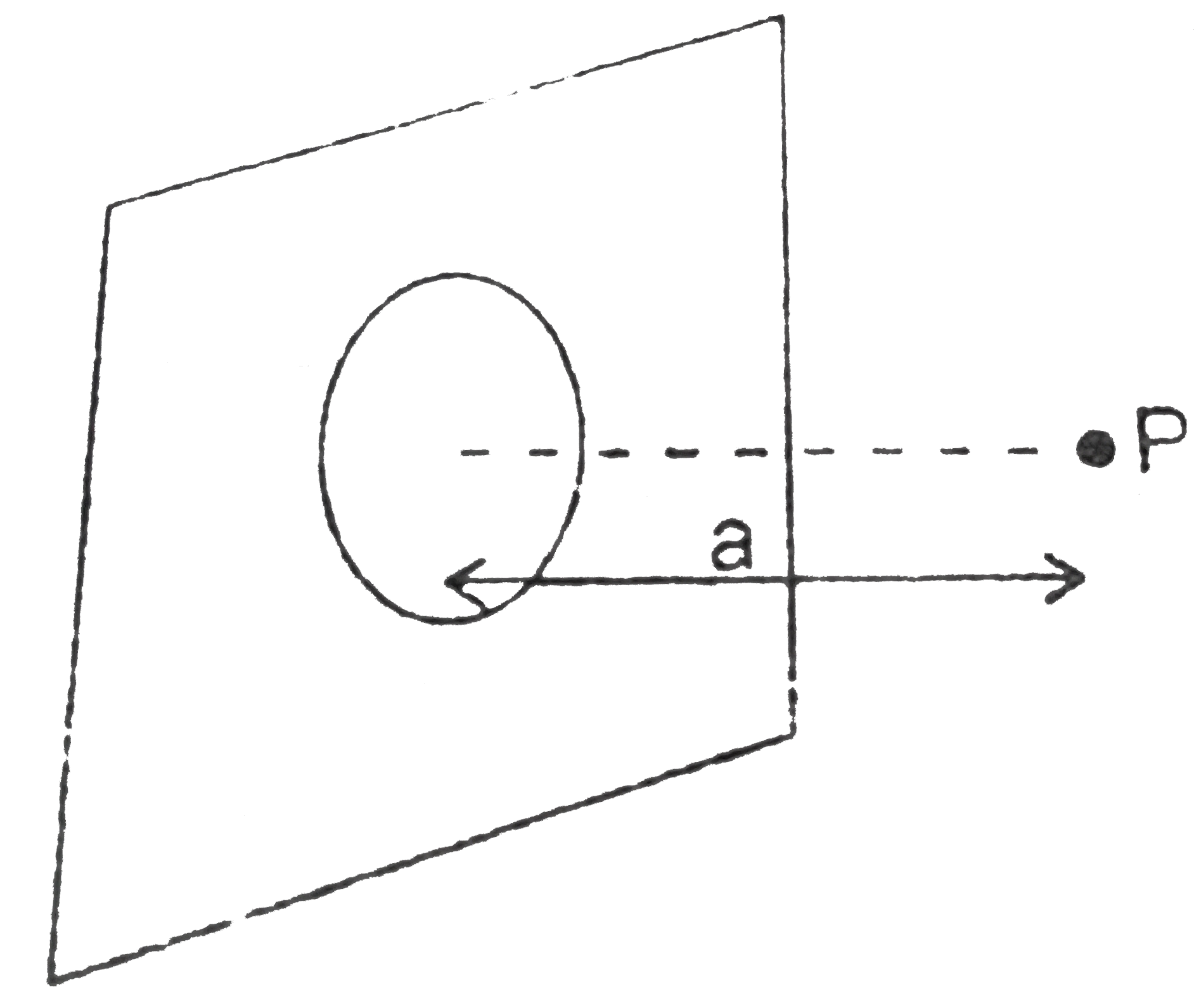
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA long cylindrical volume (of radius R) contains a uniformly distributed charge of density ρ. Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :

View SolutionThree large conducting sheets placed parallel to each other at a finite distance contain charges Q,−2Q,and3Q, respectively. Find the electric fields at points A, B, C, and D.
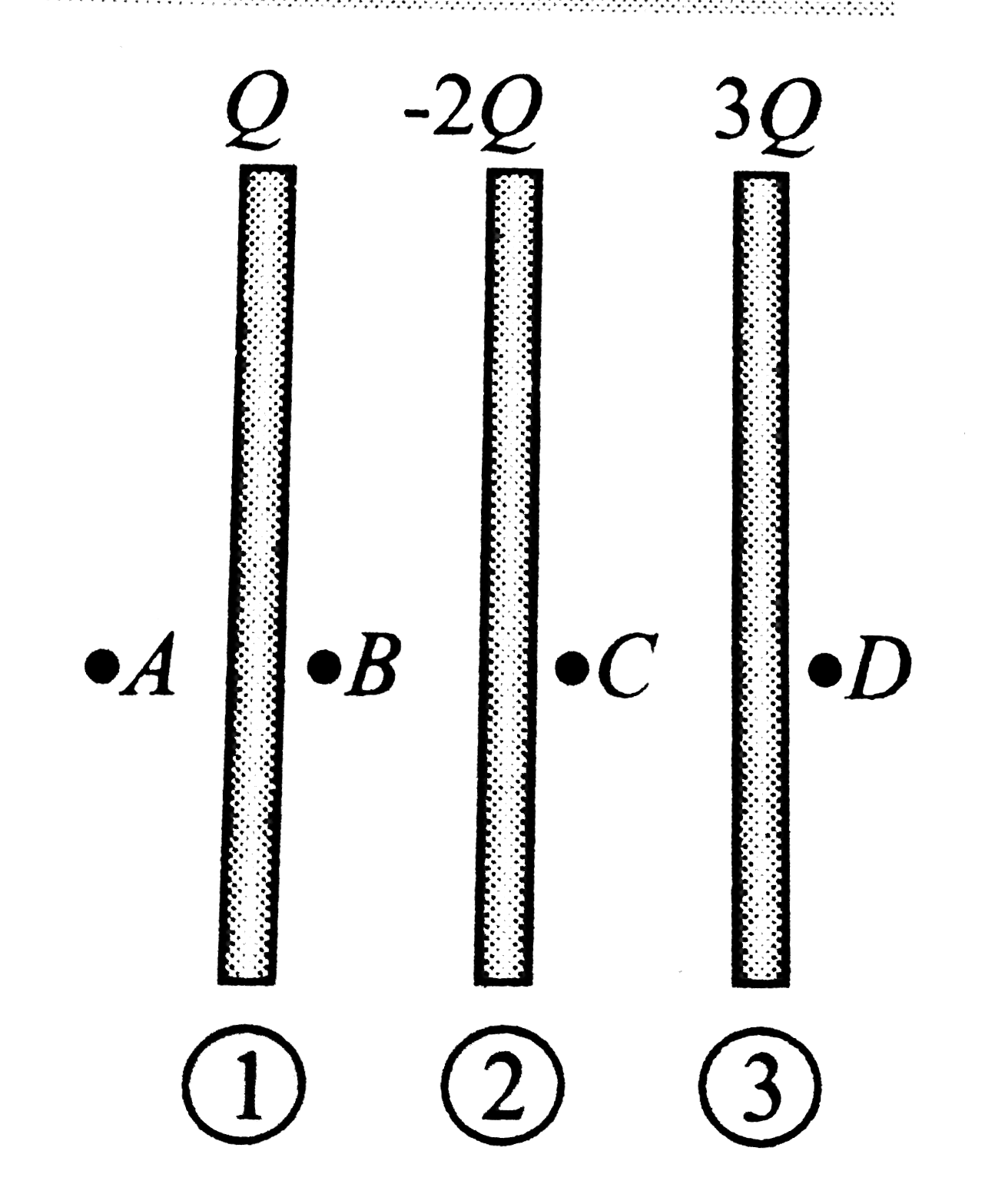
View SolutionConsider the Gaussian surface that surrounds parts of the charge distribution shown in figure. Then the contribution to the electric field at point P arises from charges

View Solution
