A number of capacitors each of capacitance 1μF and each one of which get punctured if a potential difference just exceeding 500 volt is applied, are provided. Then an arrangement suitable for giving a capacitor of 2μF across which 3000 volt may be applied requires at least-
6 component capacitors
12 component capacitors
72 component capacitors
2 component capacitors
The correct Answer is:C
To solve the problem, we need to determine the minimum number of capacitors required to create a capacitance of 2μF that can withstand a voltage of 3000V without exceeding 500V across each individual capacitor.
1. Understanding the Capacitor Configuration:
- We can arrange the capacitors in series and parallel combinations. Let m be the number of capacitors in series and n be the number of such series connected in parallel.
2. Voltage Distribution in Series:
- When m capacitors are connected in series, the total voltage VT across them is distributed equally among the capacitors. Therefore, the voltage across each capacitor V0 is given by:
V0=VTm
- Given that VT=3000V and V0 must not exceed 500V, we have:
3000m≤500
3. Calculating m:
- Rearranging the inequality gives:
m≥3000500=6
- Therefore, we need at least m=6 capacitors in series.
4. Capacitance of Series Configuration:
- The equivalent capacitance C1 of m capacitors in series is given by:
1C1=1C+1C+…+1C=mC
- For m=6 and C=1μF:
C1=Cm=1μF6=16μF
5. Total Capacitance with Parallel Configuration:
- If we have n branches of C1 connected in parallel, the total capacitance Ctotal is:
Ctotal=n⋅C1=n⋅16μF
- We want Ctotal=2μF:
n⋅16=2
6. Calculating n:
- Rearranging gives:
n=2⋅6=12
7. Total Number of Capacitors:
- The total number of capacitors N required is:
N=m⋅n=6⋅12=72
Final Answer:
The minimum number of capacitors required is 72.
---
- We can arrange the capacitors in series and parallel combinations. Let m be the number of capacitors in series and n be the number of such series connected in parallel.
- When m capacitors are connected in series, the total voltage VT across them is distributed equally among the capacitors. Therefore, the voltage across each capacitor V0 is given by:
V0=VTm
- Given that VT=3000V and V0 must not exceed 500V, we have:
3000m≤500
- Rearranging the inequality gives:
m≥3000500=6
- Therefore, we need at least m=6 capacitors in series.
- The equivalent capacitance C1 of m capacitors in series is given by:
1C1=1C+1C+…+1C=mC
- For m=6 and C=1μF:
C1=Cm=1μF6=16μF
- If we have n branches of C1 connected in parallel, the total capacitance Ctotal is:
Ctotal=n⋅C1=n⋅16μF
- We want Ctotal=2μF:
n⋅16=2
- Rearranging gives:
n=2⋅6=12
- The total number of capacitors N required is:
N=m⋅n=6⋅12=72
The minimum number of capacitors required is 72.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Three capacitors with capacitances of 1μF,2μFand3μF are connected in series. Each capacitor gets punctured, if a potential difference just exceeding 100 volt is applied. If the group is connected across 220 volt circuit then the capacitor most likely to puncture first is
View SolutionThe capacitor of capacitance 4μF and 6μF are connected in series. A potential difference of 500 volts applied to the outer plates of the two capacitor system. Then the charge on each capacitor is numerically
View Solution
Knowledge Check
The potential difference between points A and B is
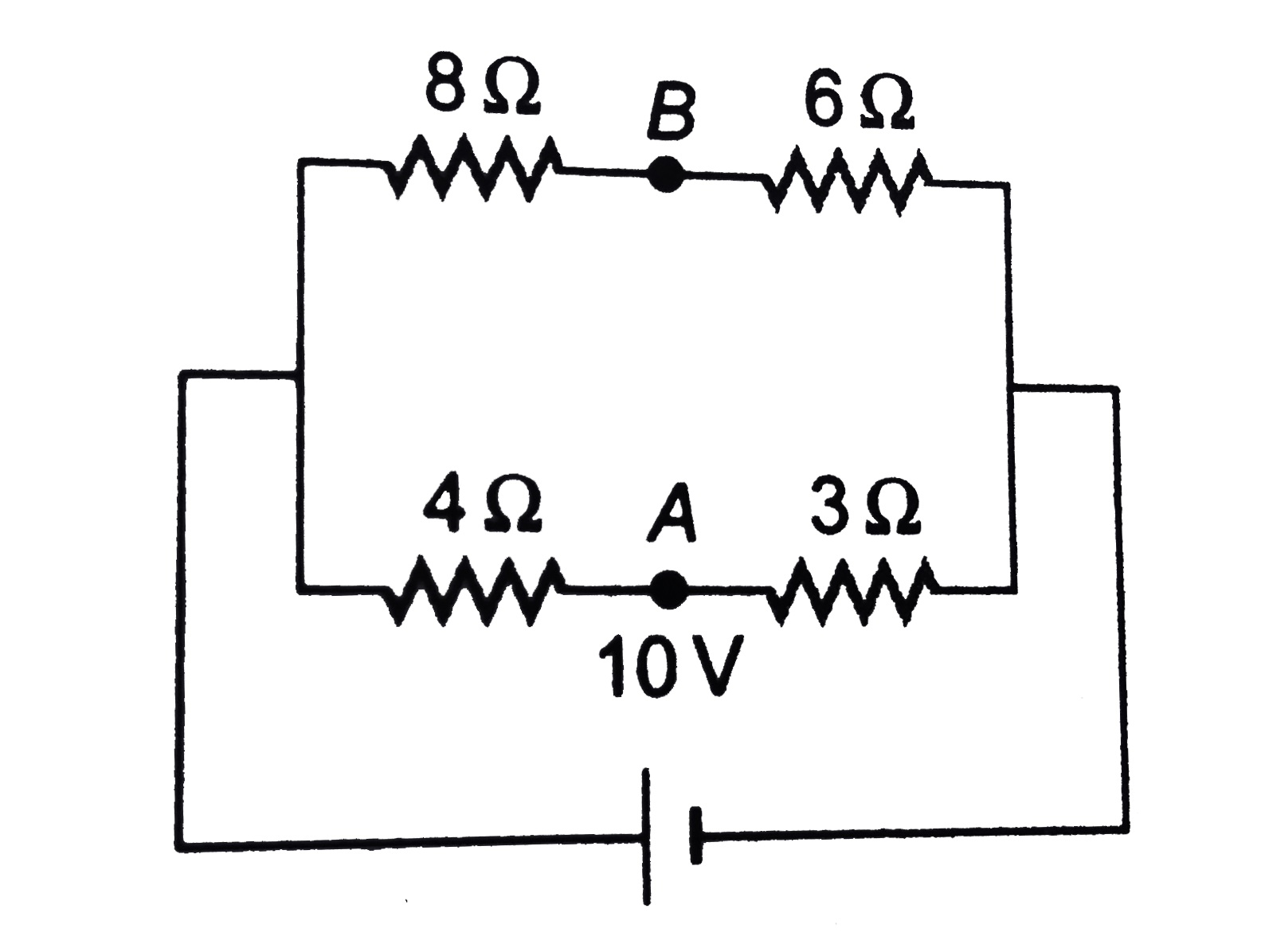 A2B5C11D18
A2B5C11D18
Six 1μF capacitors are so arranged that their equivalent capacitance is 0.70μF. If a potential difference of 600 volt is applied to the combination, what charge will appear on each capacitor ?
View SolutionA capacitor has a capacitance of 7.28μF. What amount of charge must be placed on each of its plates to make the potential difference between its plates equAl to 25.0V?
View SolutionRows of capacitors 1,2,4,8…..∞ capacitors, each of capacitance 2μF, are connected in parallel as shown in figure. The potential difference across AB = 10 V, then

View SolutionOne plate of a capacitor of capacitance 2μF has total charge +10μC and its other plate has total charge +40μC. The potential difference between the plates is (in Volt).
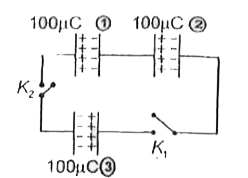
View SolutionThree identical charged capacitors each of capacitance 5 μF are connected as shown in figure. Potential difference across capacitor (3), long time after the swithces K1andK2 are closed , is
View SolutionA parallel plate capacitor of capacitance 1μF has a charge of +2μC on one of the plates and a charge of +4μC on the other. The potential difference developed across the capacitor is
View SolutionThree capacitors 3μF,6μF and 6μF are connected in series to source of 120 V. The potential difference in volt, across the 3μF capacitor will be
View Solution
