(a) Obtain lens makers formula using the expression
n2v−n1u=(n2−n1)R
Here the ray of light propagating from a rarer medium of refractive index (n1) to a denser medium of refractive index (n2) is incident on the convex side of sperical refracting surface of radius of curvature R.
(b) Draw a ray diagram to show the umage formation by concave mirror when the object is kept between its focus and the pole. Using this diagram, derive the magnification formula for the image formed.
Solution
(a) Derivation of Lens Maker's Formula
To derive the lens maker's formula, we start with the given expression:
n2v−n1u=n2−n1R
Where:
- n1 is the refractive index of the rarer medium (air).
- n2 is the refractive index of the denser medium (lens).
- u is the object distance (measured from the lens).
- v is the image distance (measured from the lens).
- R is the radius of curvature of the lens surface.
1. First Surface Refraction:
- For the first surface of the lens, we can write:
n2v1−n1u=n2−n1R1
Here, v1 is the image distance formed by the first surface.
2. Second Surface Refraction:
- The image formed by the first surface acts as an object for the second surface. Hence, we can write:
n1v−n2v1=n1−n2R2
3. Combining Equations:
- Rearranging both equations, we get:
n2⋅1v1=n2−n1R1+n1u
n1⋅1v=n1−n2R2+n2v1
4. Substituting v1:
- From the first equation, express v1 in terms of u and v:
v1=n2⋅u⋅R1(n2−n1)⋅u+n1⋅R1
5. Final Lens Maker's Formula:
- By substituting v1 back into the equations and simplifying, we arrive at the lens maker's formula:
1f=(n2−n1n1)(1R1−1R2)
Where f is the focal length of the lens.
---
(b) Ray Diagram and Magnification for Concave Mirror
1. Ray Diagram:
- Draw a concave mirror with its principal axis.
- Mark the focus (F) and the pole (P) of the mirror.
- Place the object (O) between the focus and the pole.
2. Drawing Rays:
- Draw one ray parallel to the principal axis from the object, which reflects through the focus.
- Draw a second ray passing through the center of curvature (C), which reflects back on itself.
- Extend the reflected rays backward to find the point where they intersect. This intersection point is where the image (I) is formed.
3. Image Characteristics:
- The image formed is virtual, upright, and enlarged.
4. Deriving Magnification Formula:
- The magnification (m) is given by the formula:
m=hiho=−vu
Where:
- hi is the height of the image.
- ho is the height of the object.
- v is the image distance (positive for virtual images).
- u is the object distance (negative as per sign convention).
5. Final Magnification Expression:
- Since the image is virtual and upright, we can conclude:
m=vu
---
- n1 is the refractive index of the rarer medium (air).
- n2 is the refractive index of the denser medium (lens).
- u is the object distance (measured from the lens).
- v is the image distance (measured from the lens).
- R is the radius of curvature of the lens surface.
- For the first surface of the lens, we can write:
n2v1−n1u=n2−n1R1
Here, v1 is the image distance formed by the first surface.
- The image formed by the first surface acts as an object for the second surface. Hence, we can write:
n1v−n2v1=n1−n2R2
- Rearranging both equations, we get:
n2⋅1v1=n2−n1R1+n1u
n1⋅1v=n1−n2R2+n2v1
- From the first equation, express v1 in terms of u and v:
v1=n2⋅u⋅R1(n2−n1)⋅u+n1⋅R1
- By substituting v1 back into the equations and simplifying, we arrive at the lens maker's formula:
1f=(n2−n1n1)(1R1−1R2)
Where f is the focal length of the lens.
- Draw a concave mirror with its principal axis.
- Mark the focus (F) and the pole (P) of the mirror.
- Place the object (O) between the focus and the pole.
- Draw one ray parallel to the principal axis from the object, which reflects through the focus.
- Draw a second ray passing through the center of curvature (C), which reflects back on itself.
- Extend the reflected rays backward to find the point where they intersect. This intersection point is where the image (I) is formed.
- The image formed is virtual, upright, and enlarged.
- The magnification (m) is given by the formula:
m=hiho=−vu
Where:
- hi is the height of the image.
- ho is the height of the object.
- v is the image distance (positive for virtual images).
- u is the object distance (negative as per sign convention).
- Since the image is virtual and upright, we can conclude:
m=vu
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-II, DELHI BOARD
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET -III
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
When a light ray from a rarer medium is refracted into a denser medium, its
View SolutionA biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
View SolutionA ray of light passes from a medium A having refractive index 1.6 to the medium B having refractive index 1.5. The value of critical angle of medium
A is….
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionFigure shows a ray of light as it travels from medium A to medium B. Refractive index of the medium B relative to medium A is
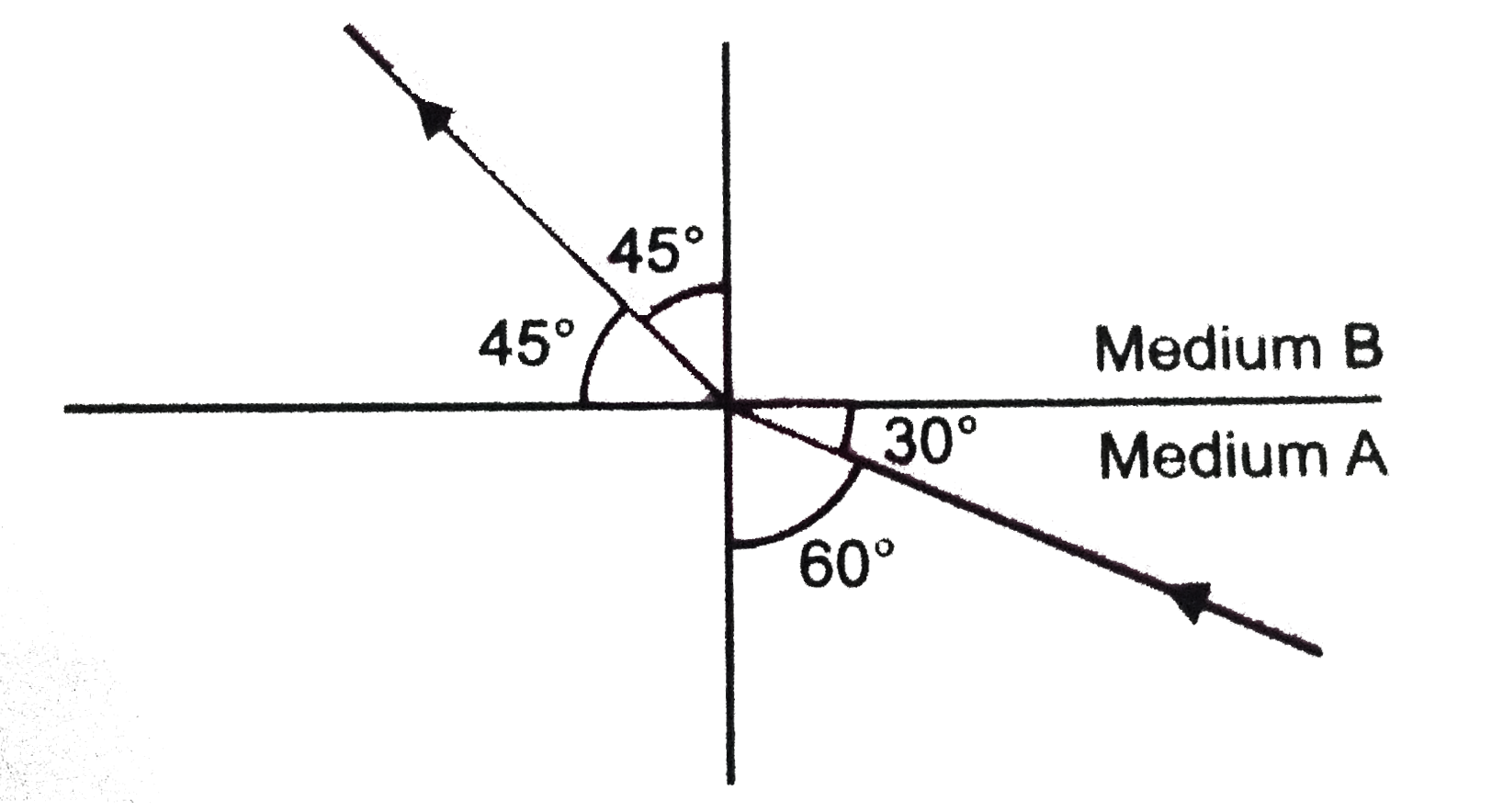
View Solution(a) For a ray of light travelling from a denser medium of refractive index n1 to a rarer medium of refractive index n2, prove that n2n1=sinic, where ic is the critical angle of incidence for the media.
(b) Explain with the help of a diagram, how the above principle is used for transmission of video signals using optical fibers.
View SolutionWhen a lens of refractive index n1, then the lens looks to be dissapeared only, if
View SolutionA denser medium of refractive index 1.5 has a concave surface of radius of curvature 12 cm. An object is situated in the denser medium at a distance of 9 cm from the pole. Locate the image due to refraction in air.
View SolutionA ray of light with wavelength 5000 nm travelling from a medium with refractive index (32) suffers partial reflection and refraction in a medium of refractive index (43). Find wavelength of reflected and refracted ray.
View SolutionIf the wavelength of light in vacuum be λ, the wavelength in a medium of refractive index n will be
View Solution
