A parallel incident beam falls on a solid glass sphere at normal incidenc. Prove that the distance of the fianll image after two refractions is at a distance (2−μ)/2(μ−1)a from the outer edge of the sphere. Refractive index of the sphere is μ and radius of the sphere is a.
To solve the problem, we need to analyze the refraction of light as it passes through a solid glass sphere. We will apply the lens maker's formula and the principles of refraction at spherical surfaces.
1. Identify the Parameters:
- Refractive index of the sphere: μ
- Radius of the sphere: a
- The incident beam is parallel and falls at normal incidence.
2. Refraction at the First Surface:
- For a parallel beam incident normally, the object distance U is taken as ∞.
- Using the lens formula for refraction, we have:
μ2V−μ1U=μ2−μ1R
- Here, μ1=1 (air), μ2=μ (glass), and R=a (radius of the sphere).
- Substituting the values, we get:
μV−0=μ−1a
- Rearranging gives:
V=μaμ−1
3. Refraction at the Second Surface:
- The light now travels from glass to air. The object distance for the second refraction is the distance from the center of the sphere to the image formed after the first refraction, which is 2a (the diameter of the sphere).
- Now, we apply the lens formula again:
1V1−μV−2a=1−μ−a
- Rearranging gives:
1V1=μV−2a+μ−1a
4. Substituting the Value of V:
- Substitute V=μaμ−1 into the equation:
1V1=μμaμ−1−2a+μ−1a
- Simplifying the first term:
μμa−2a(μ−1)μ−1=μ(μ−1)μa−2a(μ−1)=μ(μ−1)a(μ−2)
- Now, combine the two terms:
1V1=μ(μ−1)a(μ−2)+μ−1a
- Finding a common denominator gives:
1V1=μ(μ−1)+(μ−1)(μ−2)a(μ−2)
- This simplifies to:
1V1=(μ−1)(μ+μ−2)a(μ−2)=(μ−1)(2μ−2)a(μ−2)
5. Final Expression for V1:
- Therefore, we have:
V1=a(μ−2)(μ−1)(2μ−2)=a(μ−2)(μ−1)(2(μ−1))
- This leads to the final distance of the image from the outer edge of the sphere:
Distance from the outer edge=2−μ2(μ−1)a
Final Result:
The distance of the final image after two refractions is:
2−μ2(μ−1)a
- Refractive index of the sphere: μ
- Radius of the sphere: a
- The incident beam is parallel and falls at normal incidence.
- For a parallel beam incident normally, the object distance U is taken as ∞.
- Using the lens formula for refraction, we have:
μ2V−μ1U=μ2−μ1R
- Here, μ1=1 (air), μ2=μ (glass), and R=a (radius of the sphere).
- Substituting the values, we get:
μV−0=μ−1a
- Rearranging gives:
V=μaμ−1
- The light now travels from glass to air. The object distance for the second refraction is the distance from the center of the sphere to the image formed after the first refraction, which is 2a (the diameter of the sphere).
- Now, we apply the lens formula again:
1V1−μV−2a=1−μ−a
- Rearranging gives:
1V1=μV−2a+μ−1a
- Substitute V=μaμ−1 into the equation:
1V1=μμaμ−1−2a+μ−1a
- Simplifying the first term:
μμa−2a(μ−1)μ−1=μ(μ−1)μa−2a(μ−1)=μ(μ−1)a(μ−2)
- Now, combine the two terms:
1V1=μ(μ−1)a(μ−2)+μ−1a
- Finding a common denominator gives:
1V1=μ(μ−1)+(μ−1)(μ−2)a(μ−2)
- This simplifies to:
1V1=(μ−1)(μ+μ−2)a(μ−2)=(μ−1)(2μ−2)a(μ−2)
- Therefore, we have:
V1=a(μ−2)(μ−1)(2μ−2)=a(μ−2)(μ−1)(2(μ−1))
- This leads to the final distance of the image from the outer edge of the sphere:
Distance from the outer edge=2−μ2(μ−1)a
The distance of the final image after two refractions is:
2−μ2(μ−1)a
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.615videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.721videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.412videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A parallel incident beam falls on a solid glass sphere at near normal incidence.Show that the image in terms of the index of refractive μ and the sphere of radius R is given by
R(2−μ)2(μ−1)View SolutionA parallel beam falls on solid glass sphere of radius R and refractive index μ. What is the distance of final image after refractioin from two surfaces of sphere? What is the condition for the image to be real?
View SolutionA light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,r1,e and the total deviation after two refractions.
 View Solution
View SolutionA parallel beam of light falls on a solid tranparent sphere.
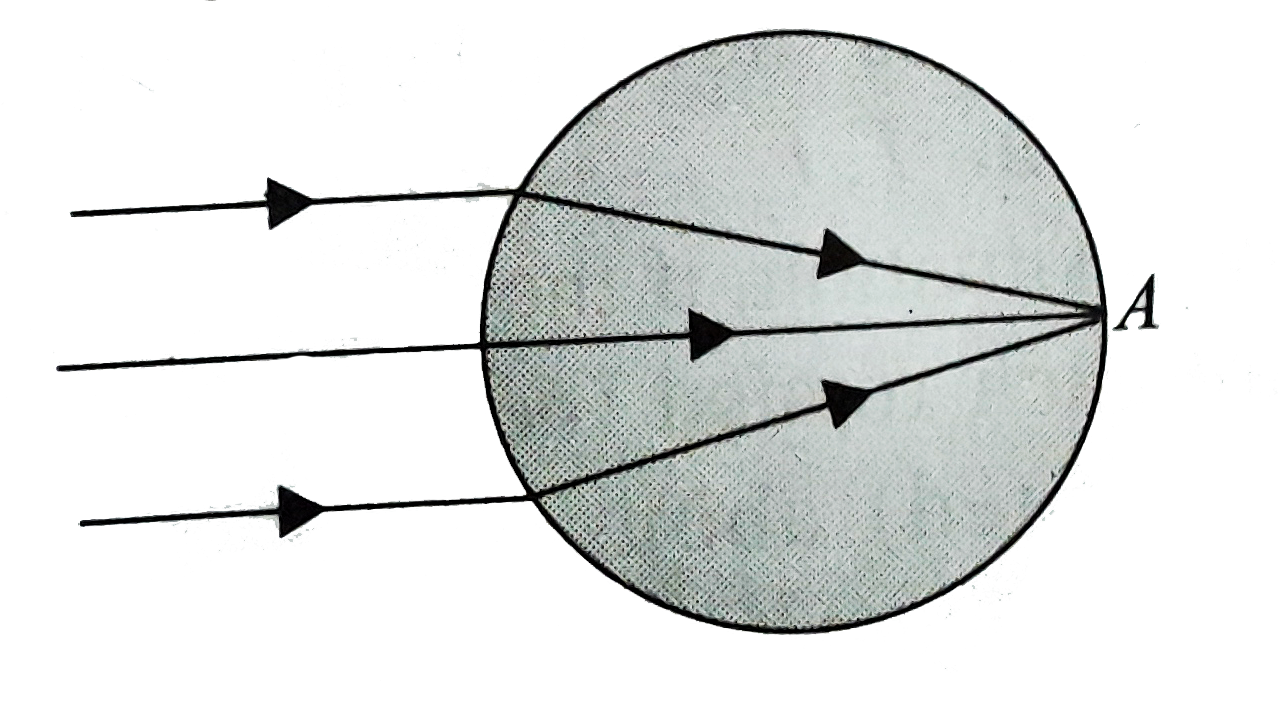
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
View SolutionA narrow parallel beam of light is incident on a transparent sphere of refractive index n if the beam finally gets focused at a point situated at a distance=2×(radius of sphere) form the center of the sphere then find n?
View SolutionA point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View SolutionA point object is situated at a distance of 36 cm from the centre of the sphere of radius 12 cm and refractive index 1.5. Locate the position of the image due to refraction through sphere.
View SolutionA horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
 if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byView Solution
if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byView Solution

