A particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)
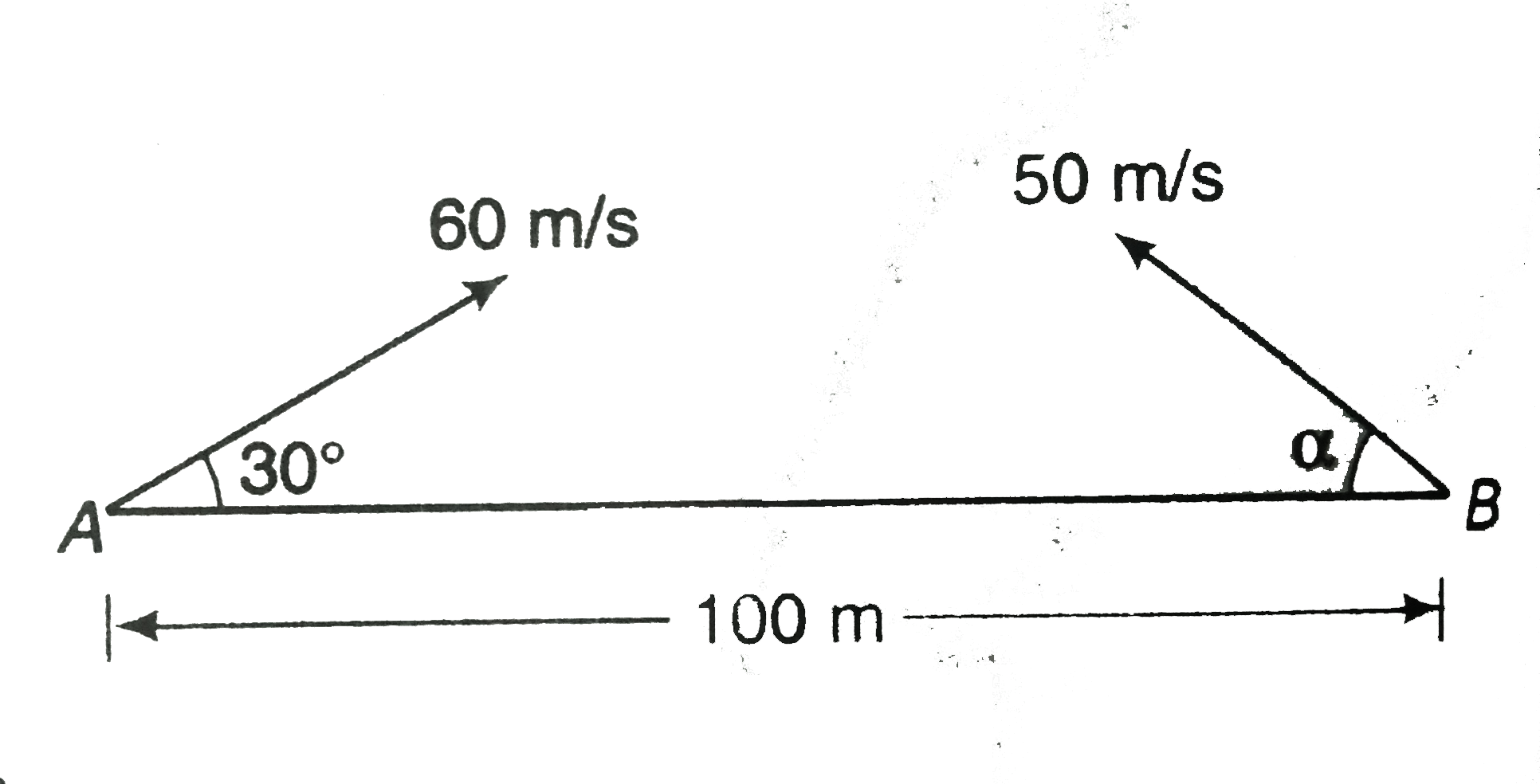
The correct Answer is:A, B, C, D
(a) Taking x and y-directions as shown in figure.
Here, aA=−gˆj
aB=−gˆj
uAx=60cos30∘=30√3m/s
uAy=60sin30∘=30m/s
uBx=−50cosα
and uBy=50sinα
Relative acceleration between the two is zero as aA=aB. Hence, the relative motion
between the two is uniform. It can be assumed that B is at rest and A is moving with uAB.
Hence, the two particles will collide, if uAB is along AB. This is possible only when
uAy=uBy
i.e. component of relative velocity along y-axis should be zero.
or 30=50sinα
∴α=sin−1(3/5)=37∘
(b) Now, |uAB|=uAx−uBx
=(30√3+50cosα)m/s
=(30√3+50×45)m/s
=(30√3+40)m/s
Therefore, time of collision is
t=AB|uAB|=10030√3+40
or t=1.09s
(c) Distance of point P from A where collision takes place is
d=√(uAxt)2+(uAyt−12>2)2
=
⎷(30√3×1.09)2+(30×1.09−12×10×1.09×1.09)2
or d=62.64m .
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 1
1 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 2
1 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
Two particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View SolutionA particle is projected at an angle θ with an initial speed u.
View SolutionA particle is projected upwards with a velocity of 100m/s at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/s2.
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA particle is projected with speed 10m/s at angle 60∘ with the horizontal. Then the time after which its speed becomes half of initial.
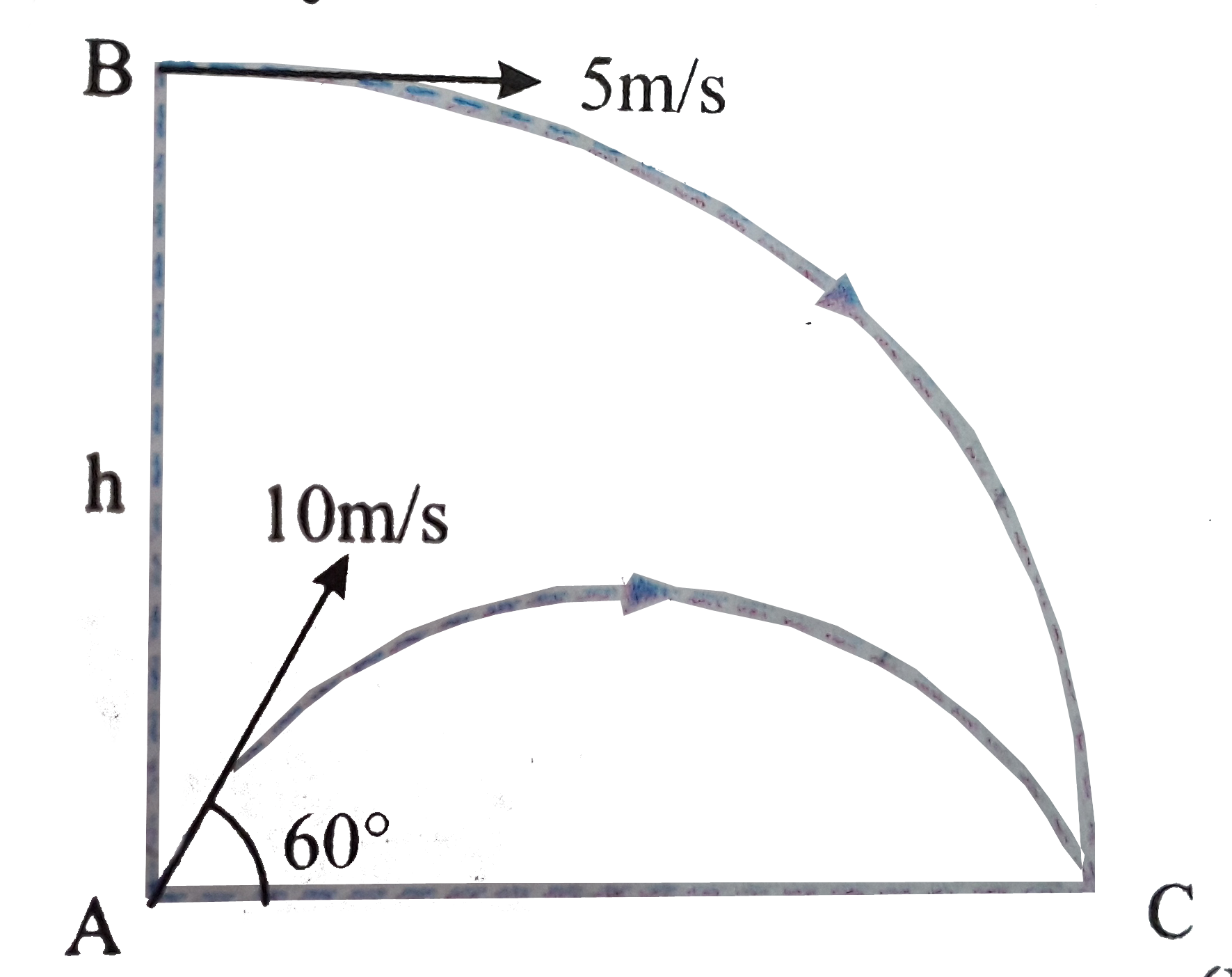
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View Solution
