A particle at origin starts towards positive direction of x-axis, with an accelerationa. This acceleration can be defined in three ways,(a) a= constant, (b) a=f(x), and (c) a=−f(t). Find the velocity of the particle as a function of time. Also find velocity of the particle when it is at a displacement x from origin. Given that the velocity of the particle at t=0 is v=w.
Step by step video & image solution for A particle at origin starts towards positive direction of x-axis, with an accelerationa. This acceleration can be defined in three ways,(a) a = constant, (b) a = f(x), and (c) a = -f (t). Find the velocity of the particle as a function of time. Also find velocity of the particle when it is at a displacement x from origin. Given that the velocity of the particle at t = 0 is v = w. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Practice Exercise
96 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Discussion Question
18 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
Similar Questions
The acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

View SolutionA particle is at rest at x=a. A force →F=bx2→i begins to act on the particle. The particle starts its motion, towards the origin, along X - axis. Find the velocity of the particle, when it reaches a distance x from the origin.
View Solution
Knowledge Check
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A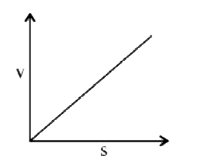 B
B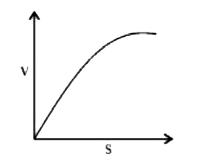 C
C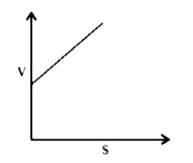 D
D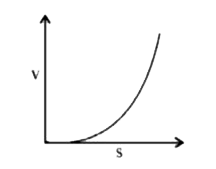
A particle is at rest at x=a. A force →F=bx2→i
begins to act on the particle. The particle starts its motion, towards the origin, along X-axis. Find the velocity of the particle, when it reaches a distance x from the origin .
View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionA particle experience an acceleration a=(4e−3t)ms2 along positive x-axis, where t is time in s .If the initial velocity of the particle is 2m/s along positive x-axis,the velocity of the particle when its acceleration becomes zero is?
View SolutionThe displacement x of a particle varies with time as x=4t2–15t+25. Find the position, velocity and acceleration of the particle at t = 0.
View SolutionThe acceleration of a particle is given by the relation as a=−kv5/2 , where is a constant. The particle starts at x=0 with a velocity of 16 m/s, and when x = 6, the velocity is observed to be 4 m/s. Find the velocity of particle when x=5m and the time at which the velocity ofthe particle is 9 m/s.
View SolutionA particle starts from rest at the origin and moves along the positive x direction. Its acceleration a versus position x graph is shown in the figure. The velocity of the particle at x = 6 m is?
View SolutionA particle moves along the x-direction with constant acceleration. The displacement, measured from a convenient position, is 2 m at time t=0 and is zero when t=10s. If the velocity of the particle is momentary zero when t=6s, determine the acceleration a and the velocity v when t=10s.
View Solution
