A particle is at rest at $x = a$ . A force $\to F = \frac{b}{x^{2}} \to i$
begins to act on the particle. The particle starts its motion, towards the origin, along X-axis. Find the velocity of the particle, when it reaches a distance x from the origin .

Video Solution

Text Solution

Verified by Experts

$F = - \frac{b}{x^{2}} \Rightarrow \frac{d}{d t} \Rightarrow (p) = - \frac{b}{x^{2}}$
$\frac{d}{d t} (m v) = - \frac{b}{x^{2}} \Rightarrow m \frac{d v}{d x} \frac{d x}{d t} = - \frac{b}{x^{2}}$
$m v d v = - \frac{b}{x^{2}} d x \Rightarrow v d v = - \frac{b}{m x^{2}} d x$
$v \int 0 v d v = x \int a - \frac{b}{m x^{2}} d x \Rightarrow \frac{v^{2}}{2} = \frac{b}{m} {[\frac{1}{x}]}_{a}^{x}$
$\frac{v^{2}}{2} = \frac{b}{m} [\frac{1}{x} - \frac{1}{a}] ∴ u = \sqrt{\frac{2 b}{m} (\frac{a - x}{x a})}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle starts from rest x = - 2.25 m and moves along the x - axis with the v - t graph as shown. The time when the particle crosses the origin is :

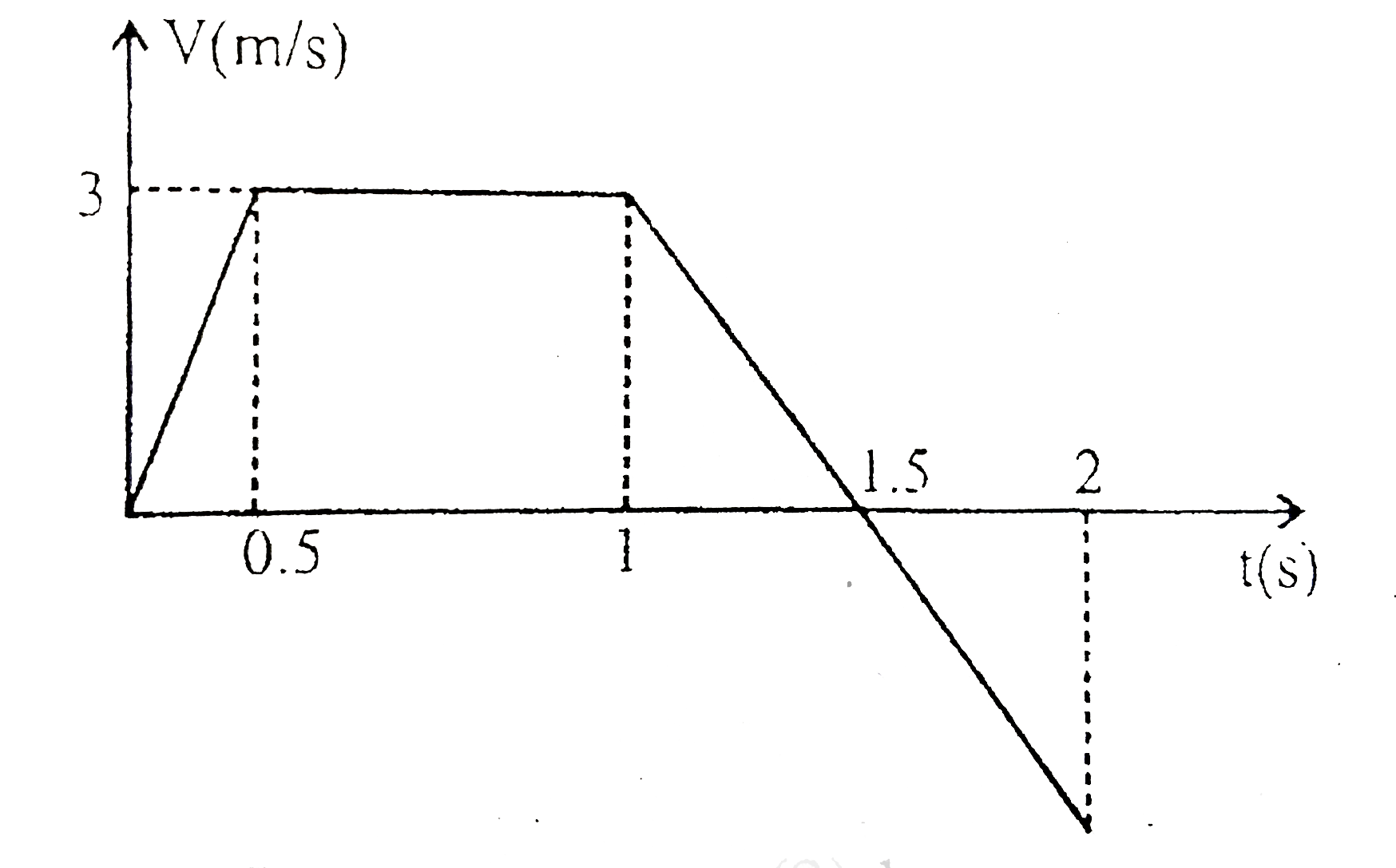A0.5 s
B1 s
C1.5 s
D2 s
Question 2 - Select One

A particle mass parallel to x-axis with constant velocity $v$ as shown in the figure. The angular velocity of the particle about the origin O
Aremains constant
Bcontinuously increases
Ccontinuously decreases
Doscillates.
Question 3 - Select One
A particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
Adecreases with time
Bincreases with time
Cremains constant
Dis zero

NARAYNA-NEWTONS LAWS OF MOTION-PASSAGE TYPE QUESTION

Home
Ask Doubt
Profile