A particle is moving along x-axis. At time Its x-coordinate is Its velocity-time equation is where, v is in m//s and t in seconds.
(a) At how many times, particle is at a distance of from the origin?
(b) Find those times.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will analyze the motion of the particle based on the given information.
Given:
- Initial position of the particle at t=0: x0=−4m
- Velocity-time equation: v=8−2t
Part (a): At how many times is the particle at a distance of 8 m from the origin?
1. Determine the positions where the particle is 8 m from the origin:
The particle can be at two positions:
- x=8m (to the right of the origin)
- x=−8m (to the left of the origin)
2. Calculate the total displacement required to reach these positions:
- For x=8m:
Displacement=xfinal−xinitial=8−(−4)=12m
- For x=−8m:
Displacement=xfinal−xinitial=−8−(−4)=−4m
3. Determine the number of times the particle crosses these positions:
The particle will cross x=8m twice (once while moving away from the origin and once while returning) and x=−8m once. Thus, the particle is at a distance of 8 m from the origin a total of three times.
Part (b): Find those times.
1. Finding times for x=8m:
Use the equation of motion:
s=ut+12at2
where:
- s=12m
- u=8m/s (initial velocity)
- a=−2m/s2 (acceleration)
Plugging in the values:
12=8t−12⋅2t2
Simplifying:
12=8t−t2
Rearranging:
t2−8t+12=0
Factoring:
(t−2)(t−6)=0
Thus, t1=2s and t2=6s.
2. Finding time for x=−8m:
Use the same equation of motion:
s=−4m
Plugging in the values:
−4=8t−12⋅2t2
Simplifying:
−4=8t−t2
Rearranging:
t2−8t−4=0
Using the quadratic formula:
t=−b±√b2−4ac2a=8±√64+162=8±√802=8±4√52
Thus:
t3=4±2√5≈8.47s
Final Times:
- The particle is at a distance of 8 m from the origin at:
- t1=2s
- t2=6s
- t3≈8.47s
Summary:
(a) The particle is at a distance of 8 m from the origin three times.
(b) The times are approximately t=2s,6s, and 8.47s.
- Initial position of the particle at t=0: x0=−4m
- Velocity-time equation: v=8−2t
The particle can be at two positions:
- x=8m (to the right of the origin)
- x=−8m (to the left of the origin)
- For x=8m:
Displacement=xfinal−xinitial=8−(−4)=12m
- For x=−8m:
Displacement=xfinal−xinitial=−8−(−4)=−4m
The particle will cross x=8m twice (once while moving away from the origin and once while returning) and x=−8m once. Thus, the particle is at a distance of 8 m from the origin a total of three times.
Use the equation of motion:
s=ut+12at2
where:
- s=12m
- u=8m/s (initial velocity)
- a=−2m/s2 (acceleration)
12=8t−12⋅2t2
Simplifying:
12=8t−t2
Rearranging:
t2−8t+12=0
Factoring:
(t−2)(t−6)=0
Thus, t1=2s and t2=6s.
Use the same equation of motion:
s=−4m
Plugging in the values:
−4=8t−12⋅2t2
Simplifying:
−4=8t−t2
Rearranging:
t2−8t−4=0
Using the quadratic formula:
t=−b±√b2−4ac2a=8±√64+162=8±√802=8±4√52
Thus:
t3=4±2√5≈8.47s
- The particle is at a distance of 8 m from the origin at:
- t1=2s
- t2=6s
- t3≈8.47s
(a) The particle is at a distance of 8 m from the origin three times.
(b) The times are approximately t=2s,6s, and 8.47s.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Miscellaneous Example
12 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise 6.1
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 6
1 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A particle is moving along x-axis. Its X-coordinate varies with time as, X=2t2+4t−6 Here, X is in metres and t in seconds. Find average velocity between the time interval t=0→t=2s.
View SolutionThe position x of a particle moving along x - axis at time (t) is given by the equation t=√x+2, where x is in metres and t in seconds. Find the work done by the force in first four seconds
View SolutionThe motion of a particle moving along x-axis is represented by the equation dvdt=6−3v, where v is in m/s and t is in second. If the particle is at rest at t = 0 , then
View SolutionA particle moves along a straight line and its velocity depends on time as v=3t−t2. Here, v is in m/s and t in second. Find
(a) average velocity and
(b) average speed for first five seconds.
View SolutionA particle is moving along x-y plane. Its x and y co-ordinates very with time as x=2t2andy=t3 Here, x abd y are in metres and t in seconds. Find average acceleration between a time interval from t=0 to t=2s.
View SolutionAcceleration of particle moving along the x-axis varies according to the law a=−2v, where a is in m/s2 and v is in m/s. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of time t.
(b) Find its position x as function of time t.
(c) Find its velocity v as function of its position coordinates.
(d) find the maximum distance it can go away from the origin.
(e) Will it reach the above-mentioned maximum distance?
View SolutionThe position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The velocity of the body at time t = 3s is
View SolutionTwo particles are moving along x-axis. Their x-coordinate versus time graph are as shown below.
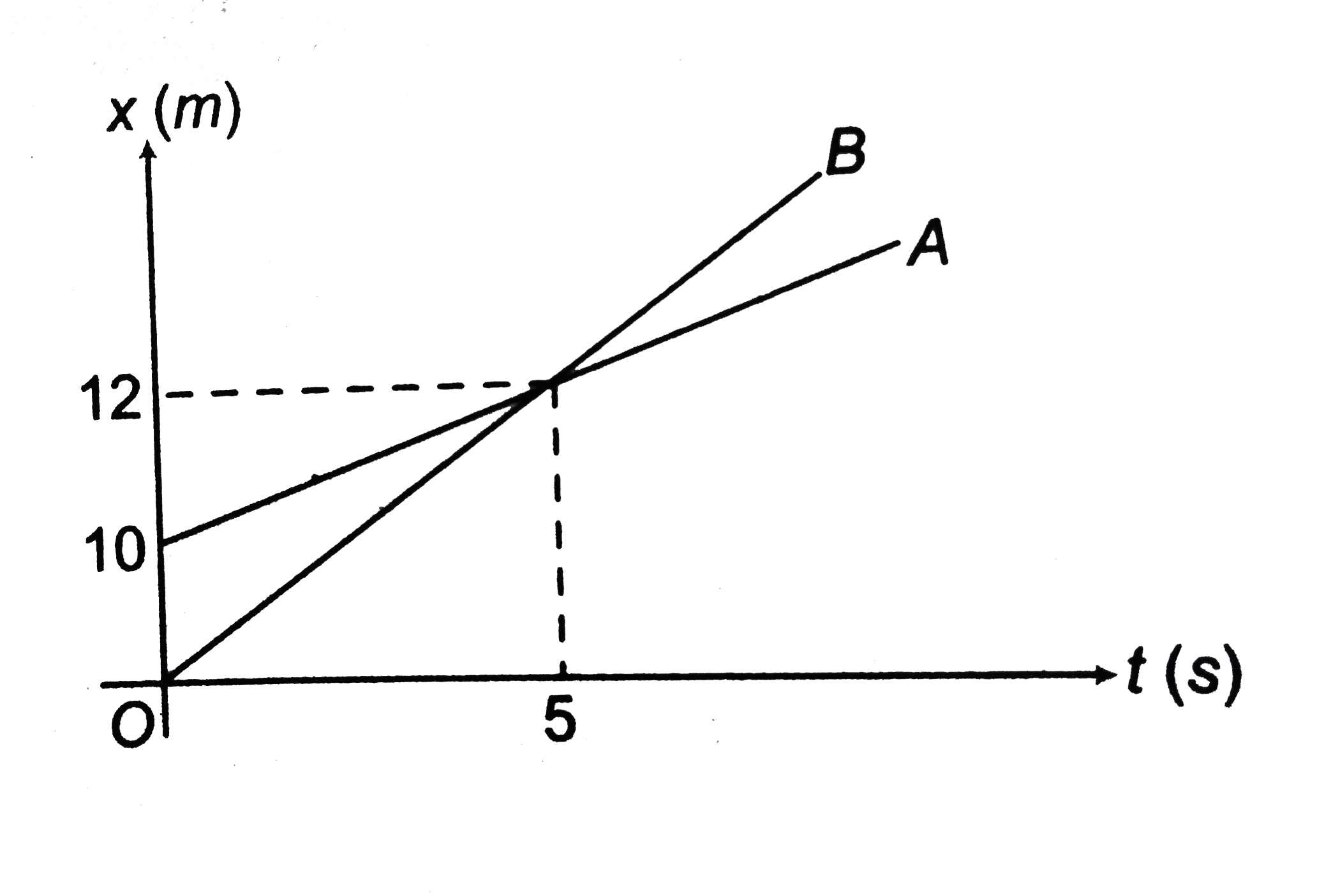
Find velocity of A w.r.t. B
View SolutionVelocity of particle moving along positive x-direction is v=(40−10t)m/s. Here,t is in seconds. At time t=0, tha x coordinate of particle is zero. Find the time when the particle is at a distance of 60 m from origin.
View SolutionA particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
View Solution
