a particle is moving in a straight line such that its velocity varies is given by v=10−2t, where v isin the first 8 second.
This problem can be solved by drawing the v-t graph.
v=10−2t
t=0,v=10m/s
t=8s,v=−6m/s
v=0⇒10−2t=0⇒t=5s
Shape: y=10−2x (straight line)
y=c+mx
c=10, +ve
m=−2, -ve
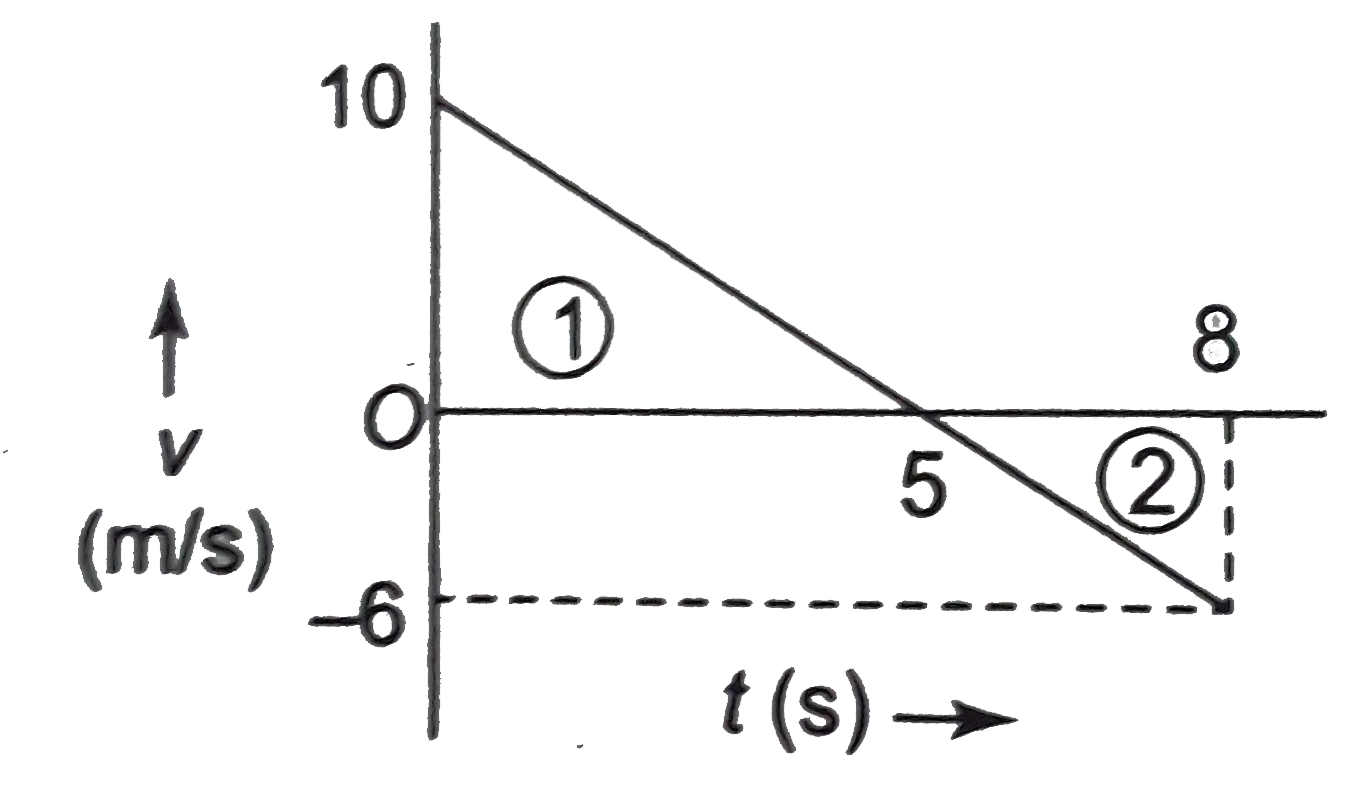
Area(1)=25,Area(2)=9
The area of the v-t graph gives the displacement//distance
Displacement=25−9−16m
Displacement=25+9=34m
Topper's Solved these Questions
Similar Questions
A particle in moving in a straight line such that its velocity is given by v=12t−3t2, where v is in m//s and t is in seconds. If at =0, the particle is at the origin, find the velocity at t=3s.
View SolutionA particle of mass 2 kg is moving in a straight line such that its velocity is given by v=3t2(m)/(s), where t is in second. Find the work done by all forces in the first 2 s of its motion.
View Solution
Knowledge Check
- Question 1 - Select One
A particle moves in a straight line so that its velocity at any point is given by v2=a+bx, where a,b≠0 are constants. The acceleration is
AzeroBuniformCnon-uniformDindeterminate - Question 2 - Select One
The acceleration of a particle moving along a straight line at any time t is given by a = 4 - 2v, where v is the speed of particle at any time t The maximum velocity is
A4 m/sB2 m/sC6 m/sDInfinity - Question 3 - Select One
Forces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
AKVtBK2V2t2CK2VtD3Kt2V
A particle is moving in a straight line such that its velocity varies as v=v0e−λt, where λ is a constant. Find average velocity during the time interval in which the velocity decreases from v0 to v02.
View SolutionThe acceleration of a particle moving along a straight line at any time t is given by a = 4 - 2v, where v is the speed of particle at any time t The maximum velocity is
View SolutionA particle moves along a straight line and its velocity depends on time as v=3t−t2. Here, v is in m/s and t in second. Find
(a) average velocity and
(b) average speed for first five seconds.View SolutionA particle moves along a straight line and its velocity depends on time as v=3t−t2. Here, v is in m/s and t in second. Find
(a) average velocity and
(b) average speed for first five seconds.View SolutionThe velocity v of a particle at any instant t moving in a straight line is given by v=s +1 where s meter is the distance travelled in t second what is the time taken by the particle to cover a distacne of 9m ?
View Solution

