A particle is performing simple harmonic motion of period T about a point O and it passes through a point P, where $O P = y$ with velicity v in the direction $\to O P .$ Show that the time which elapses before it returns to P again is
$(T / π) {tan}^{- 1} (\frac{v T}{2 π y})$

Text Solution

Verified by Experts

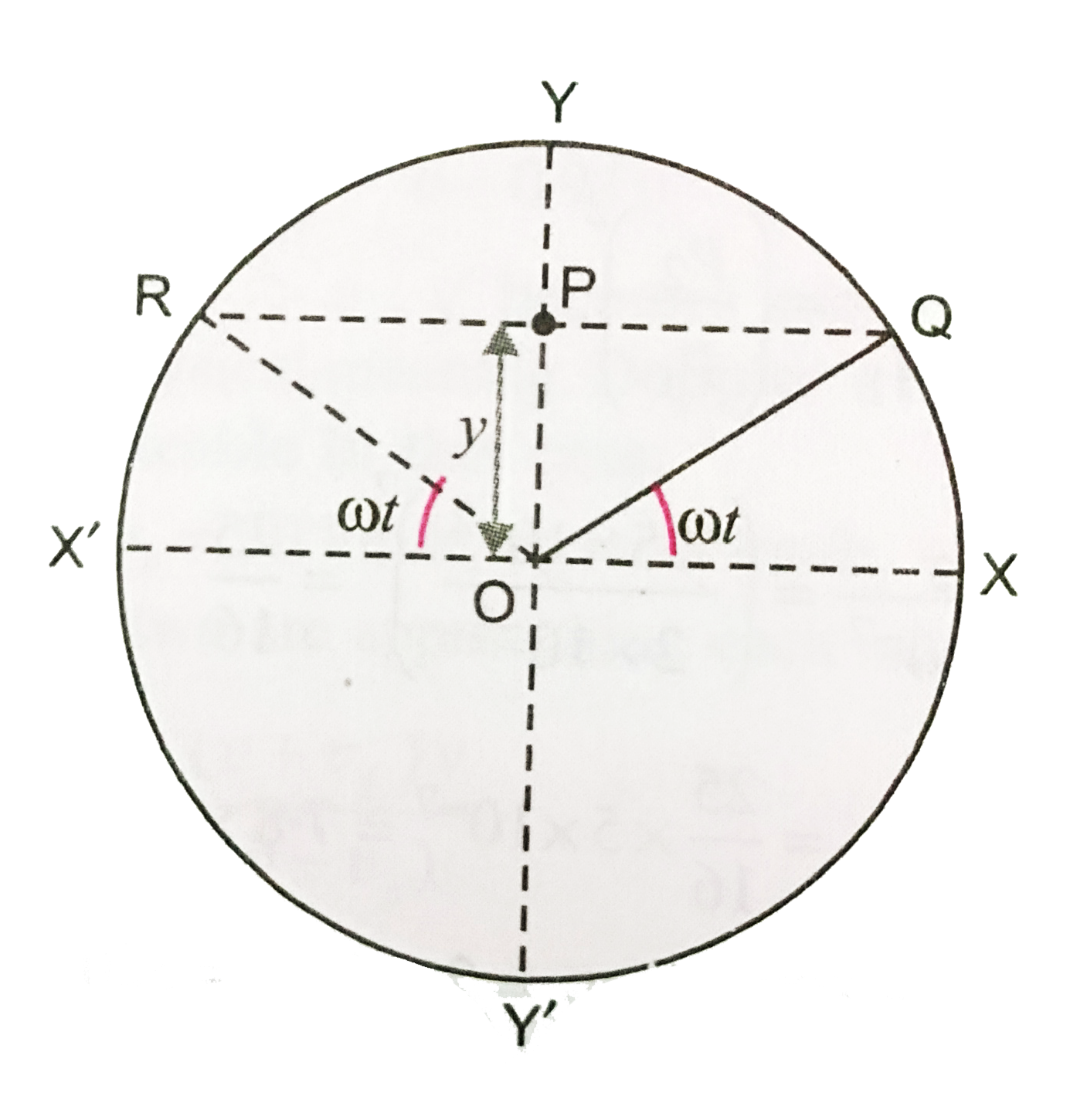
let Q and R be the positions of particle of reference on the circle of reference, corresponding to vibrating point at P in SHM, in the first instant and when it returns to p again.
Here, $y = r sin ω t$
Velocity, $v = \frac{d y}{d t} r ω cos ω t$
$∴ \frac{y}{v} = \frac{1}{ω} tan ω t or tan ω t = \frac{ω y}{v}$
or $ω t = {tan}^{1} (\frac{ω y}{v})$
Required time, $t = \frac{∠ Q O P}{ω} = \frac{2 (90^{\circ} - ω t)}{ω}$
$= \frac{2 [90^{\circ} - {tan}^{- 1} (\frac{ω y}{v})]}{ω} = \frac{2 {tan}^{- 1} (\frac{v}{ω y})}{ω}$
$= \frac{2 {tan}^{- 1} (\frac{v}{y} \times \frac{T}{2 π})}{2 π / T} = \frac{T}{π} {tan}^{- 1} (\frac{v T}{2 π y}) p r o v e d$

Updated on:21/07/2023

A particle performs simple harmonic motion about $O$ with amplitude $A$ and time period $T$ . The magnitude of its acceleration at $t = \frac{T}{8}$ s after the particle reaches the extreme position would be
A $\frac{4 π^{2} A}{\sqrt{2 T^{2}}}$
B $\frac{4 π^{2} A}{T^{2}}$
C $\frac{2 π^{2} A}{\sqrt{2 T^{2}}}$
Dnone of these
A simple pendulum performs simple harmonic motion about $x = 0$ with an amplitude a ans time period T. The speed of the pendulum at $x = \frac{a}{2}$ will be
A $\frac{π a \sqrt{3}}{2 T}$
B $\frac{π a}{T}$
C $\frac{3 π^{2} a}{T}$
D $\frac{π a \sqrt{3}}{T}$
A particle executes simple harmonic motion with a period of $16 s$ . At time $t = 2 s$ , the particle crosses the mean position while at $t = 4 s$ , its velocity is $4 m s^{- 1}$ amplitude of motion in metre is
A $\sqrt{2} π$
B $16 \sqrt{2} π$
C $24 \sqrt{2} π$
D $32 \sqrt{2} π$