A particle is projected from a point of an angle with the horizontal. At any instant t, if p is the linear momentum and E the kinetic energy, then which of the following graph is/are correct?
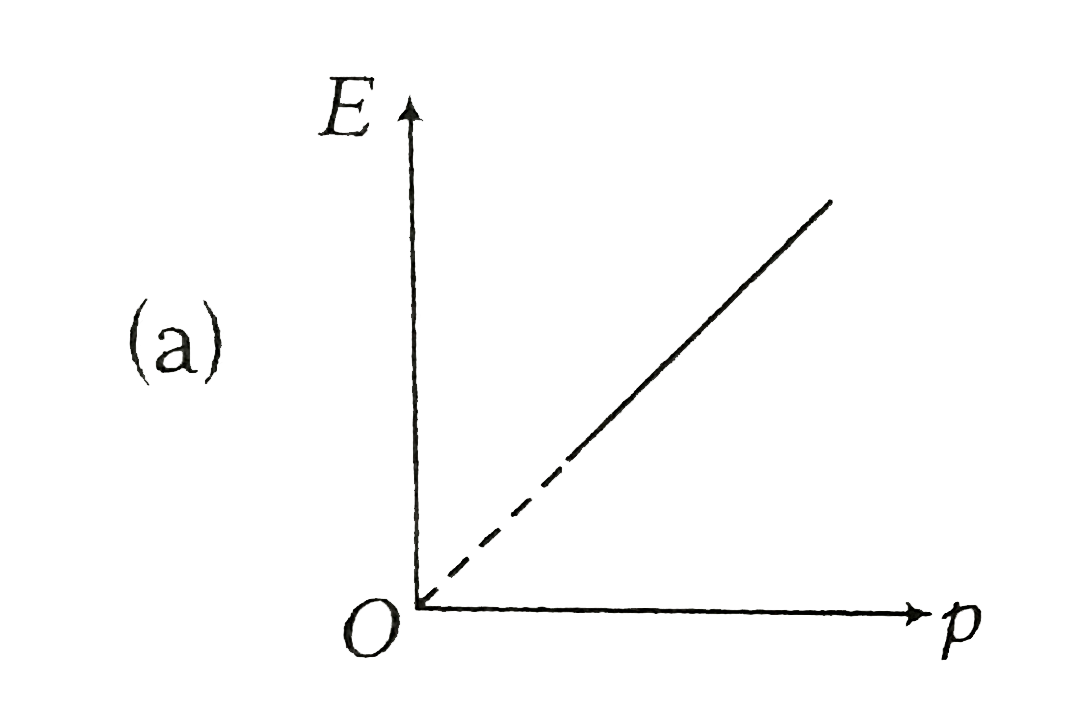
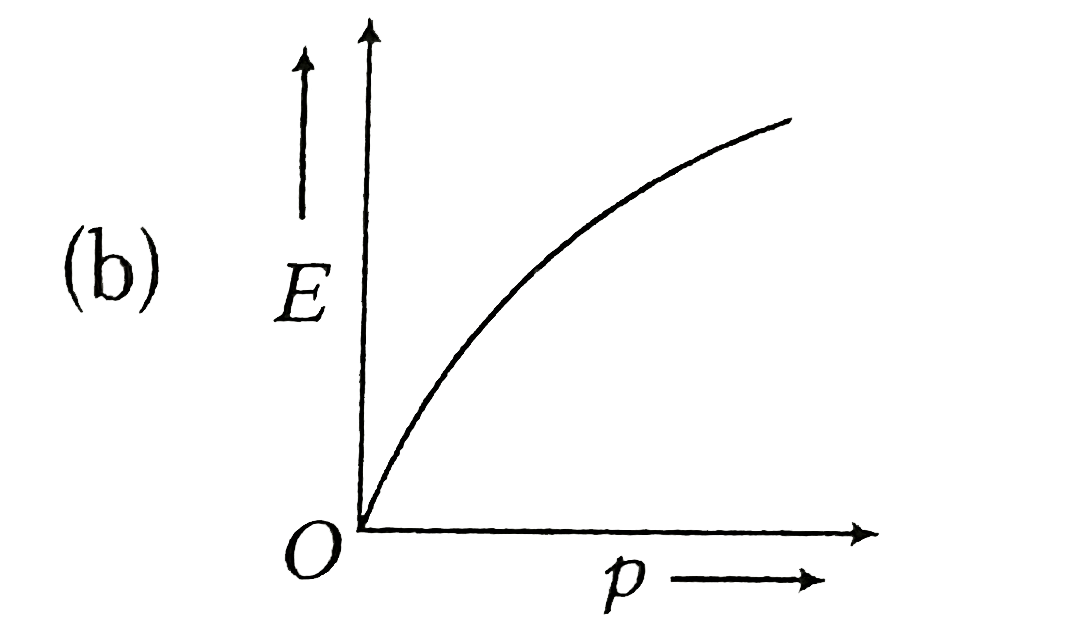

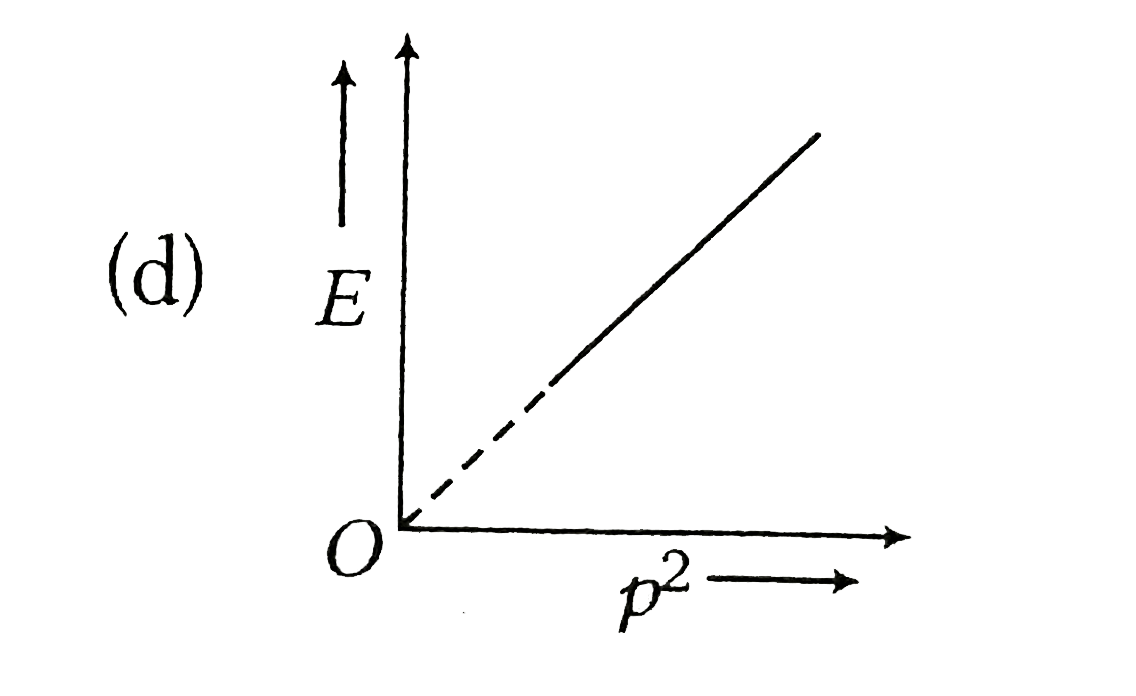
The correct Answer is:D
To solve the problem, we need to analyze the relationship between linear momentum (p) and kinetic energy (E) of a particle projected at an angle with the horizontal.
1. Understanding Linear Momentum and Kinetic Energy:
- The linear momentum (p) of a particle is given by the formula:
p=mv
where m is the mass of the particle and v is its velocity.
- The kinetic energy (E) of the particle is given by:
E=12mv2
2. Relating Kinetic Energy to Linear Momentum:
- We can express kinetic energy in terms of momentum. Since p=mv, we can solve for v:
v=pm
- Substituting this expression for v into the kinetic energy formula:
E=12m(pm)2=p22m
- This shows that kinetic energy (E) is directly proportional to the square of the momentum (p).
3. Graphical Representation:
- From the relationship E=p22m, we can deduce the nature of the graph:
- If we plot E against p2, the equation resembles y=kx (a straight line) where k=12m.
- If we plot E against p, the equation resembles y=kx2 (a parabola) because E is proportional to p2.
4. Analyzing the Options:
- Option A: Graph between E and P (should be a parabola) - False.
- Option B: Graph between E and P^2 (should be a straight line) - True.
- Option C: Graph between E and P (should be an upward parabola) - False.
- Option D: Graph between E and P^2 (should be a straight line) - True.
5. Conclusion:
- The correct graphs are those that show the relationship between kinetic energy and the square of momentum, which is a straight line through the origin. Therefore, the correct answer is the graph of E vs P^2.
Final Answer:
The correct graph is the one that represents the relationship between kinetic energy (E) and the square of momentum (P^2), which is a straight line.
- The linear momentum (p) of a particle is given by the formula:
p=mv
where m is the mass of the particle and v is its velocity.
- The kinetic energy (E) of the particle is given by:
E=12mv2
- We can express kinetic energy in terms of momentum. Since p=mv, we can solve for v:
v=pm
- Substituting this expression for v into the kinetic energy formula:
E=12m(pm)2=p22m
- This shows that kinetic energy (E) is directly proportional to the square of the momentum (p).
- From the relationship E=p22m, we can deduce the nature of the graph:
- If we plot E against p2, the equation resembles y=kx (a straight line) where k=12m.
- If we plot E against p, the equation resembles y=kx2 (a parabola) because E is proportional to p2.
- Option A: Graph between E and P (should be a parabola) - False.
- Option B: Graph between E and P^2 (should be a straight line) - True.
- Option C: Graph between E and P (should be an upward parabola) - False.
- Option D: Graph between E and P^2 (should be a straight line) - True.
- The correct graphs are those that show the relationship between kinetic energy and the square of momentum, which is a straight line through the origin. Therefore, the correct answer is the graph of E vs P^2.
The correct graph is the one that represents the relationship between kinetic energy (E) and the square of momentum (P^2), which is a straight line.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason21videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns9videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points50videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
Similar Questions
A particle is projected at an angle θ from the horizontal with kinetic energy (T). What is the kinetic energy of the particle at the highest point ?
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected with initaial velocity u at an angle 0 with horizontal, then variation of angular momentum L about starting w.r.t. Time t will be
View SolutionA particle of mass m has momentum p. Its kinetic energy will be
View SolutionA particle of mass m is projected with a velocity v making an angle of 45∘ with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.
View SolutionA particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View SolutionA particle is projected at t=0 from a point on the ground with certain velocity at an angle with the horizontal. The power of gravitation force is plotted against time. Which of the following is the best representation?
View SolutionA particle A is projected with speed VA from a point making an angle 60∘ with the horizontal. At the same instant, a second particle B is thrown vertically upwards from a point directly below the maximum height point of parabolic path of A, with velocity VB . If the two particles collide then the ratio of VA/VB should be:
View Solution

