A particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
To solve the problem of determining the angle α at which a particle should be projected from the bottom of an inclined plane (with an inclination of 30∘) to achieve maximum range, we can follow these steps:
Step 1: Understand the Problem
The inclined plane makes an angle β=30∘ with the horizontal. We need to find the angle α (the angle of projection from the horizontal) that maximizes the range of the projectile on this inclined plane.
Step 2: Set Up the Coordinate System
We will set up a coordinate system where:
- The x-axis is parallel to the inclined plane.
- The y-axis is perpendicular to the inclined plane.
Step 3: Resolve the Initial Velocity
Let u be the initial velocity of the projectile. We can resolve this velocity into two components:
- The component parallel to the incline (x-direction):
ux=ucos(α−β)
- The component perpendicular to the incline (y-direction):
uy=usin(α−β)
Step 4: Determine the Acceleration Components
The acceleration due to gravity g can also be resolved into two components:
- Parallel to the incline:
ax=−gsin(β)
- Perpendicular to the incline:
ay=−gcos(β)
Step 5: Write the Range Formula
The range R on the inclined plane can be expressed as:
R=u2gcos2(β)sin(2α−β)
This formula shows that the range depends on sin(2α−β).
Step 6: Maximize the Range
To maximize the range, we need to maximize sin(2α−β). The sine function achieves its maximum value of 1 when:
2α−β=90∘
Thus, we can rearrange this equation to find α:
2α=90∘+β
α=90∘+β2
Step 7: Substitute the Value of β
Given β=30∘:
α=90∘+30∘2=120∘2=60∘
Final Answer
The angle α at which the particle should be projected to achieve maximum range on the inclined plane is:
α=60∘
The inclined plane makes an angle β=30∘ with the horizontal. We need to find the angle α (the angle of projection from the horizontal) that maximizes the range of the projectile on this inclined plane.
We will set up a coordinate system where:
- The x-axis is parallel to the inclined plane.
- The y-axis is perpendicular to the inclined plane.
Let u be the initial velocity of the projectile. We can resolve this velocity into two components:
- The component parallel to the incline (x-direction):
ux=ucos(α−β)
- The component perpendicular to the incline (y-direction):
uy=usin(α−β)
The acceleration due to gravity g can also be resolved into two components:
- Parallel to the incline:
ax=−gsin(β)
- Perpendicular to the incline:
ay=−gcos(β)
The range R on the inclined plane can be expressed as:
R=u2gcos2(β)sin(2α−β)
This formula shows that the range depends on sin(2α−β).
To maximize the range, we need to maximize sin(2α−β). The sine function achieves its maximum value of 1 when:
2α−β=90∘
Thus, we can rearrange this equation to find α:
2α=90∘+β
α=90∘+β2
Given β=30∘:
α=90∘+30∘2=120∘2=60∘
The angle α at which the particle should be projected to achieve maximum range on the inclined plane is:
α=60∘
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Assertion And Reason10videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Single Correct16videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Exercise 7.210videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
Similar Questions
A particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particles is projected from the foot of an inclined plane having inclination 45∘ , with the velocity u at angle θ(>45∘) with the horizontal in a vertical plane containing the line of greatest slope through the point of projection. Find the value of tanθ if the particle stikes the plane.
(i) Horizontally
(ii) Normally
 View Solution
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to the horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionA ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
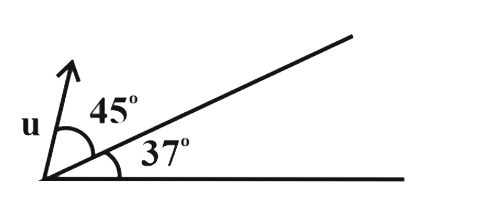
View SolutionA particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
 View Solution
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle is projected up an inclined plane of inclination β at na elevation ∝ to the horizontal. Show that
(a) tan∝=cotβ+2tanβ, if the particle strikes the plane at right angles
(b) tan∝=2tanβ, if the particle strikes the plane horizontally.View Solution

