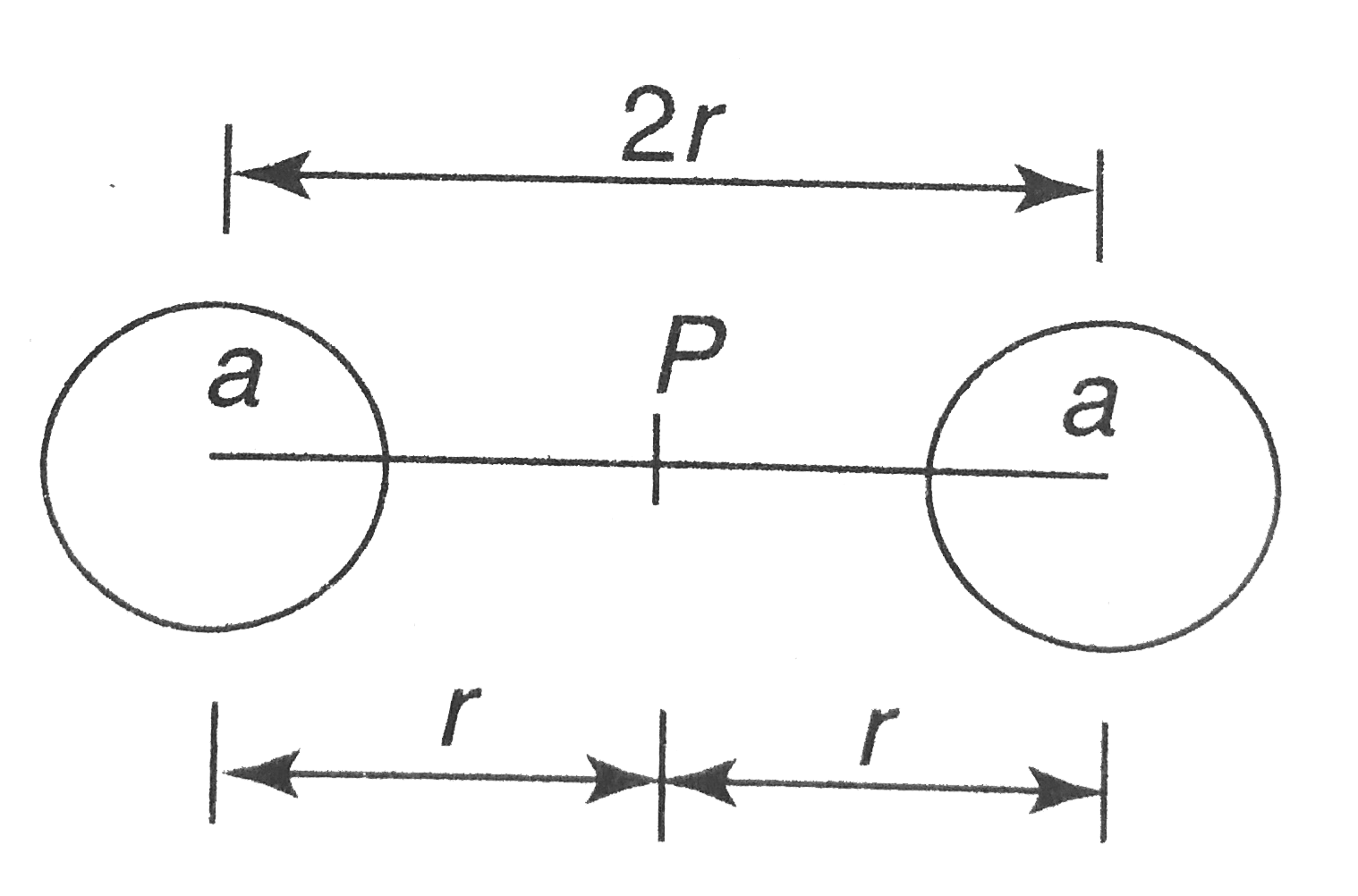
A particle is projected from the surface of one star towards other star of same radius $a$ and mass with such a minimum velocity $K \sqrt{\frac{G M}{a}}$ , so that it is attracted towards other star. Find the value of $K$ if two stars are $2 r$ distance apart:

A

$\frac{2 (r - a)}{{[r (2 r - a)]}^{1 / 2}}$

B

$\frac{2 (r - a)}{{[r (r - a)]}^{1 / 2}}$

C

$\frac{r - a}{{[r (r - a)]}^{1 / 2}}$

D

$\frac{r + a}{{[r (r - a)]}^{1 / 2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$\frac{1}{2} m v_{min}^{2} = [- \frac{G M m}{r} - \frac{G M m}{r}]$
$- [- \frac{G M m}{(2 r - a)} - \frac{G M m}{a}]$
$= \frac{2 G M m (a^{2} - 2 a r + r^{2})}{a r (2 r - a)}$
or $v_{min} = \sqrt{\frac{G M}{a}} \times \frac{2 (r - a)}{{[r (2 r - a)]}^{1 / 2}}$
So, $K = \frac{2 (r - a)}{{[r (2 r - a)]}^{1 / 2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If a particles of mass $m$ is projected with minimum velocity form the surface of a star with kinetic energy $\frac{K_{1} G M m}{a}$ and potential energy at surface of the star $\frac{K_{2} G M m}{a}$ towards the star of same mass $m$ and radius $a$ ( $K_{1}$ and $K_{2}$ are constant) to reach the other star. Find the distance between the centre of the two stars:
A $\frac{2 a}{(K_{2} - K_{1})}$
B $\frac{4 a}{(K_{2} - K_{1})}$
C $\frac{2 a}{(K_{1} - K_{2})}$
D $\frac{a}{(K_{1} - K_{2})}$
Question 2 - Select One
A pair of stars rotates about their centre of mass One of the stars has a mass $M$ and the other has mass m such that $M = 2 m$ The distance between the centres of the stars is d (d being large compared to the size of either star) .
The ratio of the angular momentum of the two stars about their common centre of mass $(L_{m} / L_{m})$ is .
A $1$
B $2$
C $4$
D $9$
Question 3 - Select One
The angular velocity of rotation of star (of mass M and radius R ) at which the matter start to escape from its equator will be
A $\sqrt{\frac{2 G M^{2}}{R}}$
B $\sqrt{\frac{2 G M}{g}}$
C $\sqrt{\frac{2 G M}{R^{2}}}$
D $\sqrt{\frac{2 G R}{M}}$

A2Z-GRAVITATION-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile