A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Fig. 2 (EP). 26)
(a) Find an expression for range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) β at which range will be maximum.
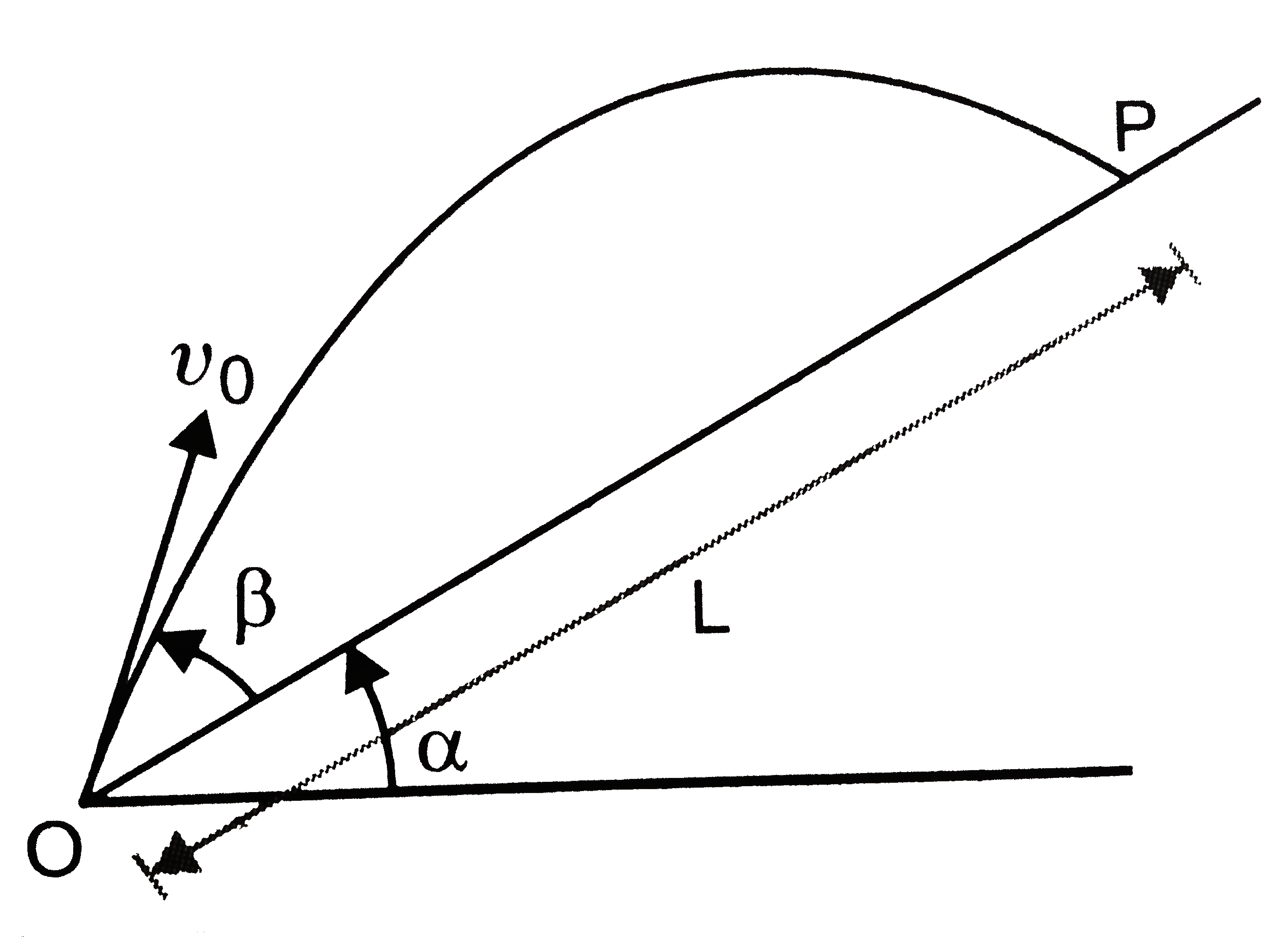
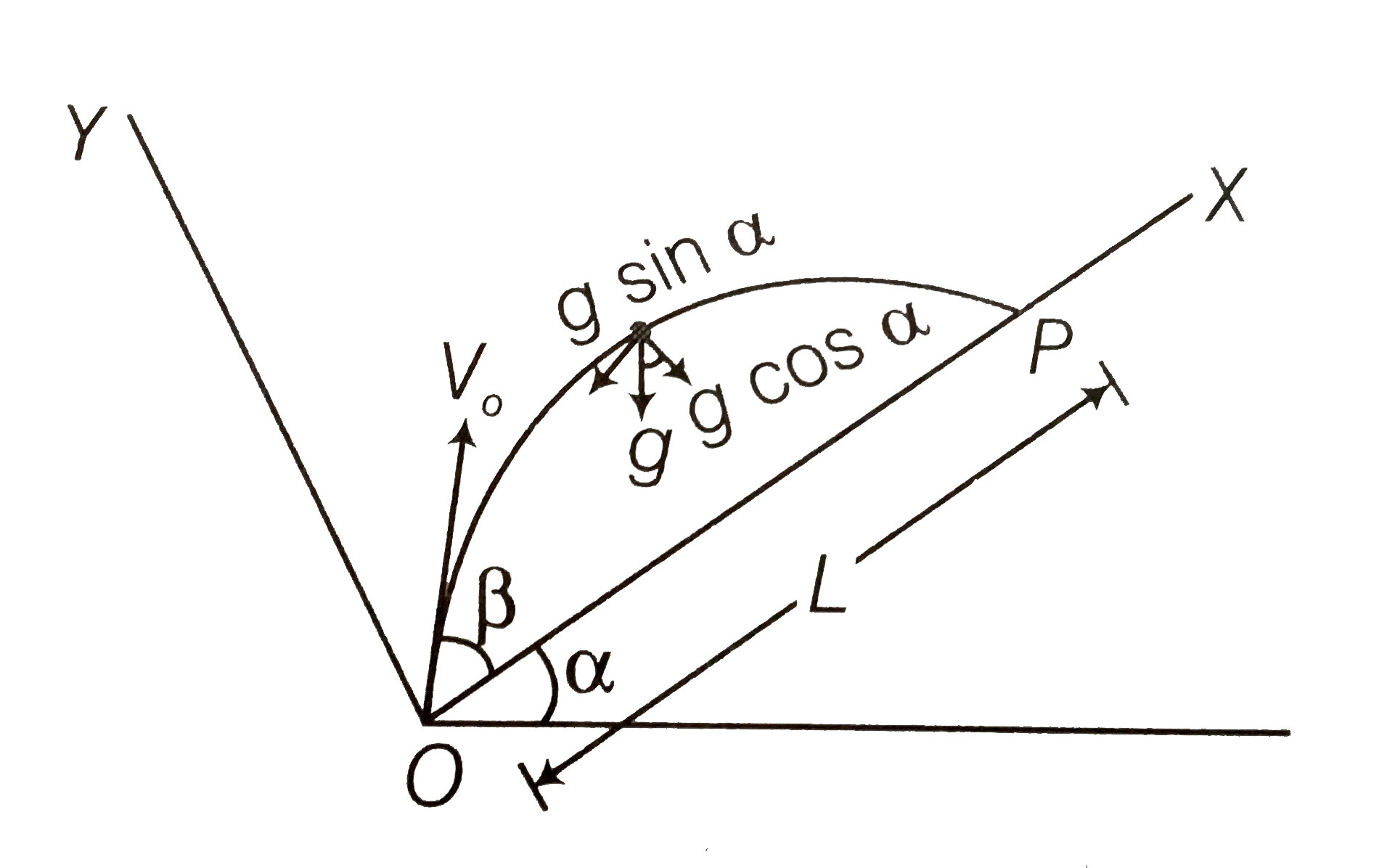
Consider the adjacent diagram.
Mutually perpendicular x and y-axes are shown in the diagram.
Particle is projected from the point O.
Let time taken in reaching from point O to point P is T.
(b) Considering motion along vertical upward direction perpendicular to OX.
For the journey O to P.
y=0,uy=v0sinβ,ay=−gcosα,t=T
Applying equation,
y=uyt+12ayt2
⇒ 0=v0sinβT+12(−gcosα)T2
⇒T[v0sinβ−gcosα2T]=0
⇒ T=0,T=2v0sinβgcosα
As T = 0, corresponding to point O
Hence, T=Time of flight=2v0sinβgcosα
(a) Considering motion along OX,
x=L,ux=v0cosβ,ax=−gsinα
t=T=2v0sinβgcosα
x=uxt+12axt2
⇒ L=v0cosβT+12(−gsinα)T2
⇒ L=v0cosβT−12gsinαT2
=T[v0cosβ−12gsinαT]
=T[v0cosβ−12gsinα×2v0sinβgcosα]
=2v0sinβgcosα[v0cosβ−v0sinαsinβgcosα]
=2v20sinβgcos2α[cosβ.cosα−sinα.sinβ]
⇒ L=2v20sinβgcos2αcos(α+β)
(c) For range (L) to be maximum.
Let, Z=sinβ.cos(α+β)
=sinβ[cosα.cosβ−sinα.sinβ]
=12[cosα.sin2β−2sinα.sin2β]
=12[sin2β.cosα−sinα(1−cos2β)]
⇒ z=12[sin2β.cosα−sinα+sinα.cos2β]
=12[sin2β.cosα+cos2β.sinα−sinα]
=12[sin(2β+α)−sinα]
For z to be maximum,
sin(2=β+α)=maximum = 1
⇒ 2β+α=π2or,β=π4−α2
Topper's Solved these Questions
Similar Questions
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA ball is projected with velocity u at right angle to the slope which inclined at an angle α with the horizontal. The distance x along the inclined plane that it will travell before again striking the slope is-
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionAn object is projected from A and reaches B on the same horizontal surface. A plane mirror inclined at an angle θ to the horizontal is placed on the ground as shown in the figure. Which of the following best describes the path of the image?

View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to the horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionTwo particles are projected at the same instant from the same point at inclinations α and β to the horizontal. If they simultaneously hit the top and bottom of a vertical pole subtending angle θ at the point of projection , find (tanα−tanβ).
View Solution
