A particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from theposition as shown in Fig. Calculate
a. the impulse developed in the string when it becorries taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
From M to N the ball will fall a distance o 4m, then impulse will be developed in the string ON.

velocity of the ball just before the string becomes tight
u0=√2×10×4=√80m/s
velocity of the ball in the direction perpendicular to the impulse will remain same (just after and just before the impulse developed.)
v=u0sinθ=√80×35=15√5m/s
J=μ0cosθ=1√80×45=16√5kgm/s
J'=Jsinθ=45√5kgm/s
and impulse given by earth
J''=Jcosθ=645√5kgm/s
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
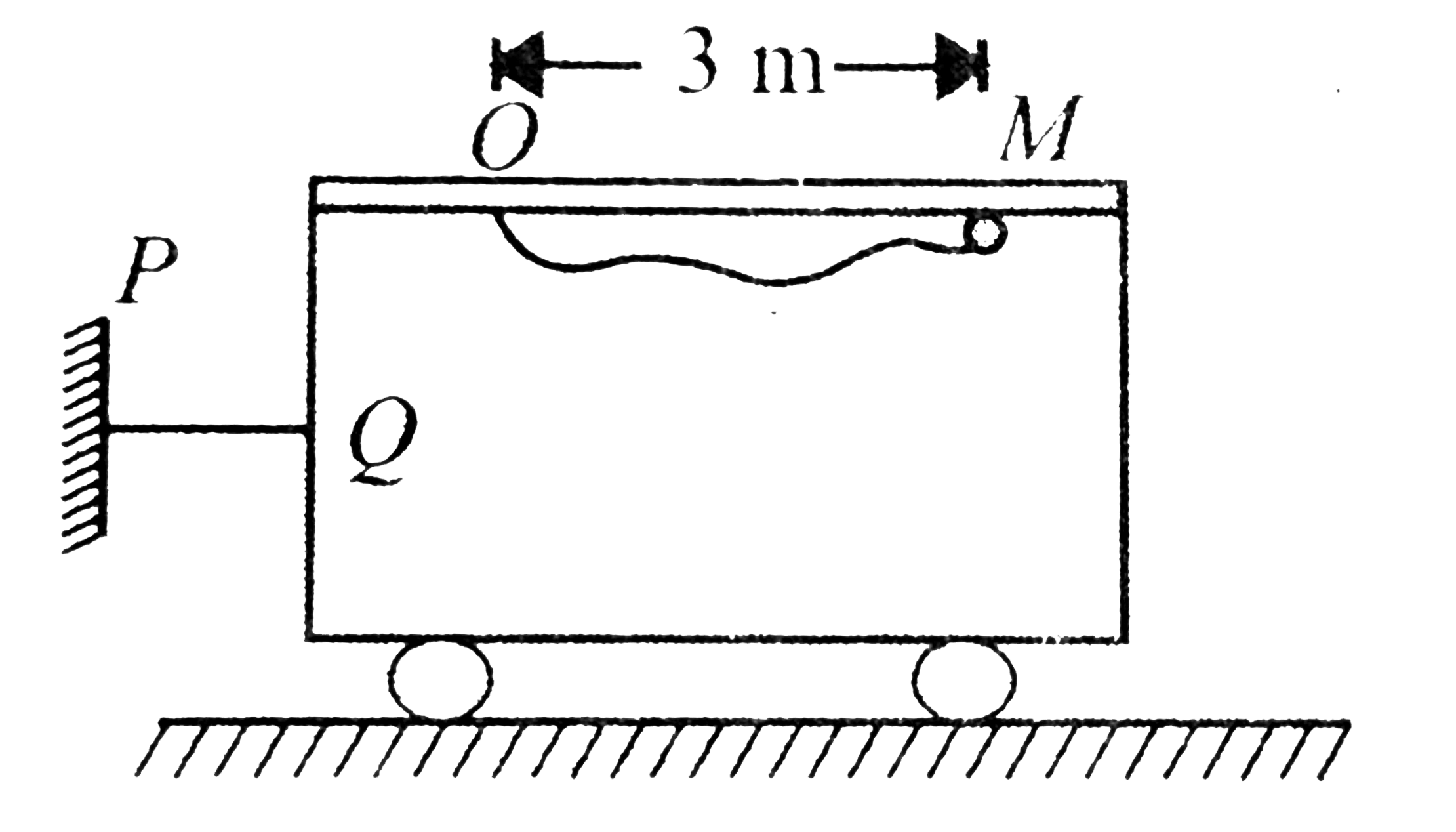
A ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take g=10m/s2)

View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
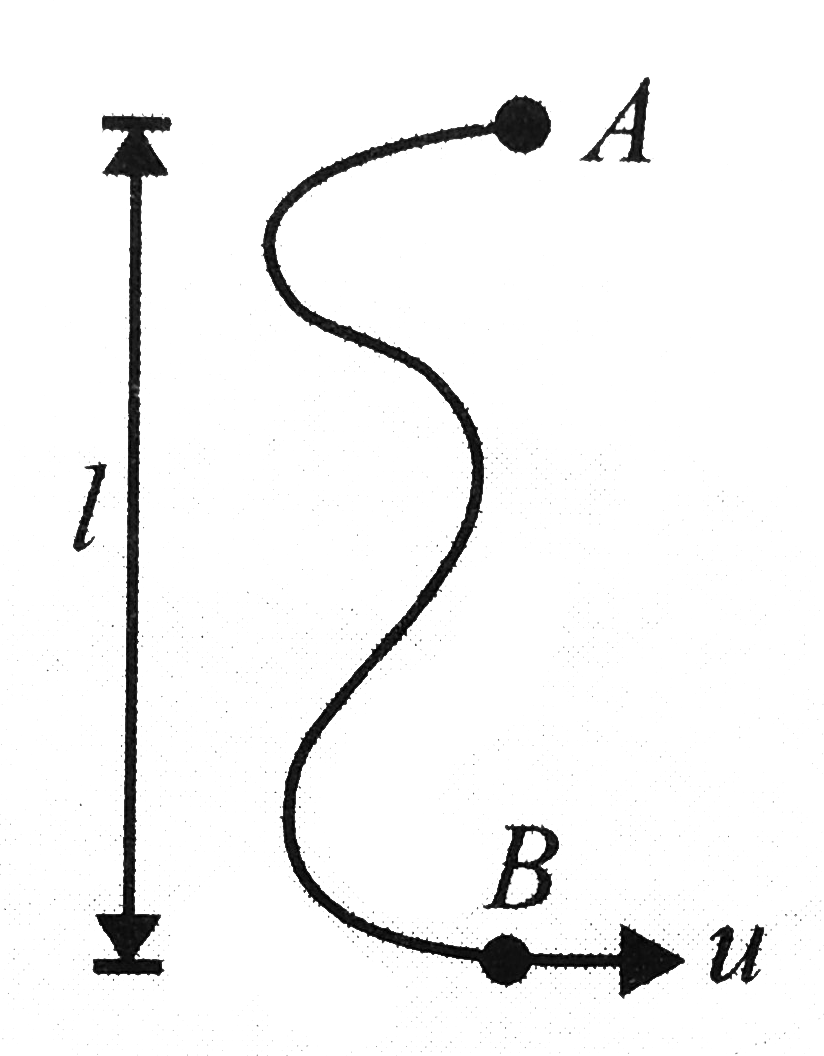
View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the position shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
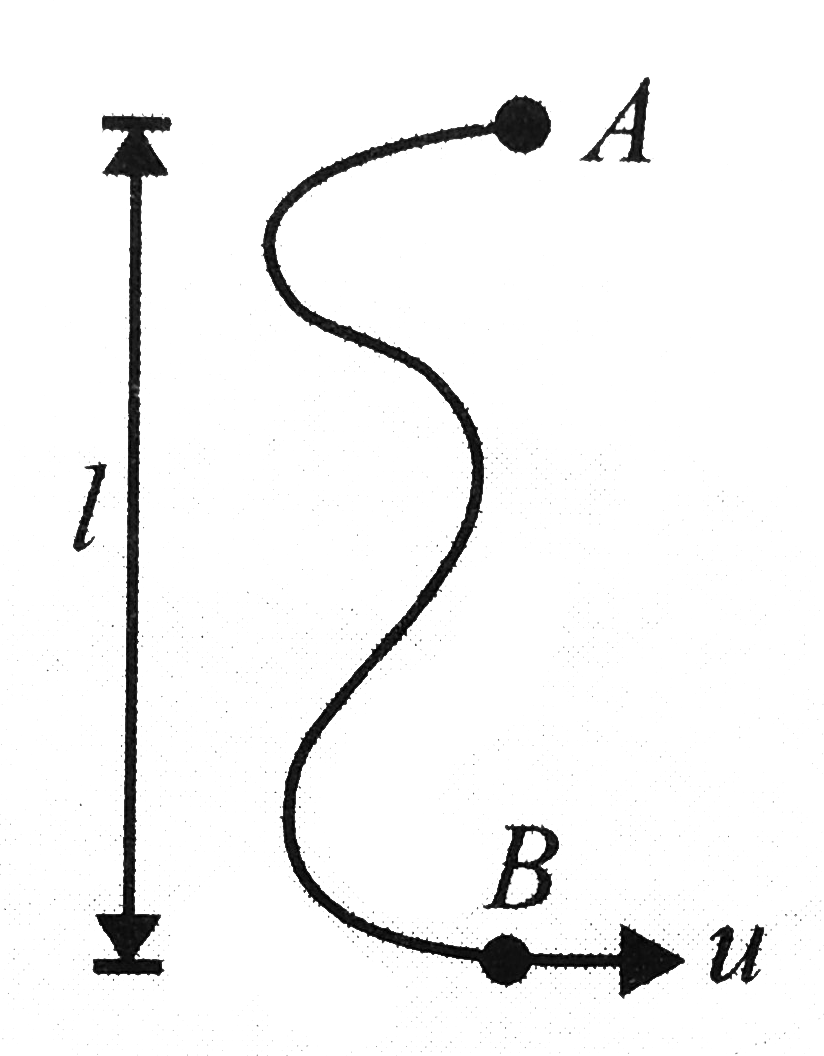
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA particle of mass m is suspended by a string of length l from a fixed rigid support. A sufficient horizontal velocity =√3gl is imparted to it suddenly. Calculate the angle made by the string with the vertical when the accekleration of the particle is inclined to the string by 45∘ .
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA stone of mass 0.5 kg is attached to a string of length 2 m and is whirled in a horizontal circle. If the string can with stand a tension of 9N, the maximum velocity with which the stone can be whirled is:
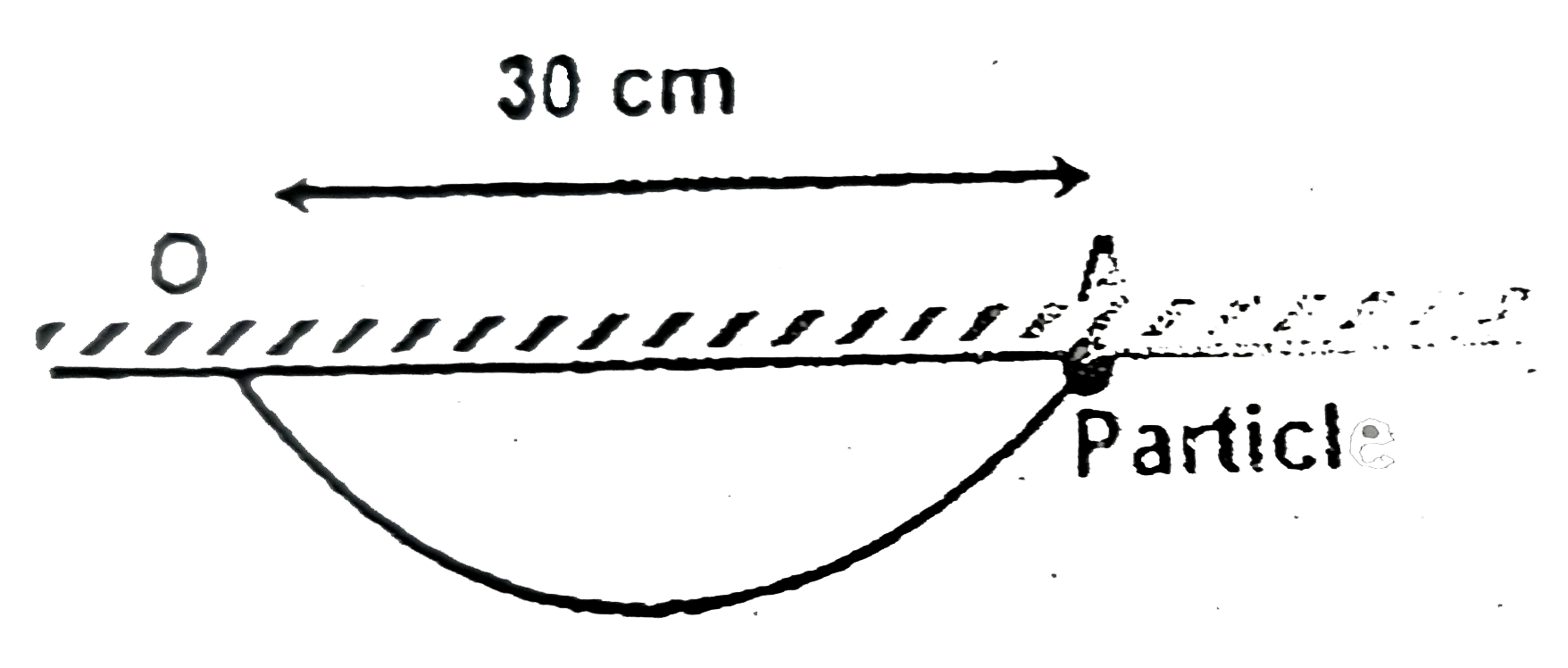
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
View SolutionA particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
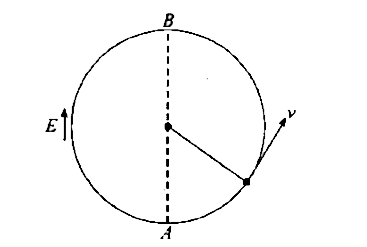
View SolutionA mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?
View Solution
