A particle of mass m is made to move with uniform speed u along the perimeter of a regular polygon of n sides. What is the magnitude of impulse applied by the particle at each corner of the polygon?
2 mv sin π2n
mv sin π2n
m v cos π2n
2 mv cos π2n
To solve the problem of finding the magnitude of impulse applied by a particle of mass m moving with uniform speed u along the perimeter of a regular polygon with n sides, we can follow these steps:
1. Understanding Impulse:
Impulse (J) is defined as the change in momentum of an object. Mathematically, it can be expressed as:
\(
J = \Delta p = p_f - p_i
\)
where \( p_f \) is the final momentum and \( p_i \) is the initial momentum.
2. Initial and Final Momentum:
Since the particle moves with uniform speed u, the initial momentum \( p_i \) and final momentum \( p_f \) at each corner of the polygon can be expressed as:
\(
p_i = mu \quad \text{and} \quad p_f = mu
\)
3. Change in Momentum:
At each corner, the direction of the velocity changes, which means the momentum vector changes direction. The magnitude of the change in momentum can be calculated using vector subtraction:
\(
J = p_f - p_i
\)
However, since both momenta have the same magnitude but different directions, we will have to consider the angle between them.
4. Angle Between Momentum Vectors:
For a regular polygon with n sides, the angle \( \theta \) between the initial and final momentum vectors at each corner is:
\(
\theta = \frac{2\pi}{n}
\)
5. Using the Law of Cosines:
The magnitude of the change in momentum can be calculated using the law of cosines:
\(
J = \sqrt{(p_f)^2 + (p_i)^2 - 2(p_f)(p_i)\cos(\theta)}
\)
Substituting \( p_f = mu \) and \( p_i = mu \):
\(
J = \sqrt{(mu)^2 + (mu)^2 - 2(mu)(mu)\cos\left(\frac{2\pi}{n}\right)}
\)
6. Simplifying the Expression:
This simplifies to:
\(
J = \sqrt{2(m^2u^2)(1 - \cos\left(\frac{2\pi}{n}\right))}
\)
\(
J = mu\sqrt{2(1 - \cos\left(\frac{2\pi}{n}\right))}
\)
7. Using the Trigonometric Identity:
We can use the identity \( 1 - \cos(x) = 2\sin^2\left(\frac{x}{2}\right) \):
\(
J = mu\sqrt{2 \cdot 2\sin^2\left(\frac{\pi}{n}\right)} = mu \cdot 2\sin\left(\frac{\pi}{n}\right)
\)
8. Final Result:
Therefore, the magnitude of the impulse applied by the particle at each corner of the polygon is:
\(
J = 2mu \sin\left(\frac{\pi}{n}\right)
\)
Impulse (J) is defined as the change in momentum of an object. Mathematically, it can be expressed as:
\(
J = \Delta p = p_f - p_i
\)
where \( p_f \) is the final momentum and \( p_i \) is the initial momentum.
Since the particle moves with uniform speed u, the initial momentum \( p_i \) and final momentum \( p_f \) at each corner of the polygon can be expressed as:
\(
p_i = mu \quad \text{and} \quad p_f = mu
\)
At each corner, the direction of the velocity changes, which means the momentum vector changes direction. The magnitude of the change in momentum can be calculated using vector subtraction:
\(
J = p_f - p_i
\)
However, since both momenta have the same magnitude but different directions, we will have to consider the angle between them.
For a regular polygon with n sides, the angle \( \theta \) between the initial and final momentum vectors at each corner is:
\(
\theta = \frac{2\pi}{n}
\)
The magnitude of the change in momentum can be calculated using the law of cosines:
\(
J = \sqrt{(p_f)^2 + (p_i)^2 - 2(p_f)(p_i)\cos(\theta)}
\)
Substituting \( p_f = mu \) and \( p_i = mu \):
\(
J = \sqrt{(mu)^2 + (mu)^2 - 2(mu)(mu)\cos\left(\frac{2\pi}{n}\right)}
\)
This simplifies to:
\(
J = \sqrt{2(m^2u^2)(1 - \cos\left(\frac{2\pi}{n}\right))}
\)
\(
J = mu\sqrt{2(1 - \cos\left(\frac{2\pi}{n}\right))}
\)
We can use the identity \( 1 - \cos(x) = 2\sin^2\left(\frac{x}{2}\right) \):
\(
J = mu\sqrt{2 \cdot 2\sin^2\left(\frac{\pi}{n}\right)} = mu \cdot 2\sin\left(\frac{\pi}{n}\right)
\)
Therefore, the magnitude of the impulse applied by the particle at each corner of the polygon is:
\(
J = 2mu \sin\left(\frac{\pi}{n}\right)
\)
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Only one option is correct for JEE Advanced
60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A particle of mass in is made to move with uniform speed v0 along the perimeter of a regular hexagon, inscribed in a circle of radius R. The magnitude of impulse applied at each corner of the hexagon is
View SolutionFind the radius of the circumscribing circle of a regular polygon of n sides each of length is a.
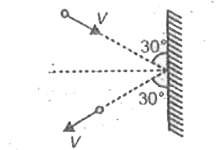
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
View SolutionA particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
View SolutionIf a regular polygon of n sides has circum radius R and inradius r then each side of polygon is:
View SolutionA particle of mass m=5 units is moving with a uniform speed v=3√2 units in the XY-plane along the y=x+4. The magnitude of the angular momentum about origin is
View SolutionA particle of mass 'm' is moving on a circular path of radius 'r' with uniform speed 'v'. Rate of change of linear momentum is
View SolutionEach side of a regular polygon is 2.5 cm in length. The perimeter of the polygon is 12.5 cm. How many sides does the polygon have?
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution
