A particle of mass m is released from a certain height h with zero initial velocity. It strikes the ground elastlcally (direction of its velocity is reversed but magnitude remains the same). Plot the graph between its kinetic energy and time till it returns to its initial position.
The correct Answer is:A, C, D
To solve the problem of plotting the graph between kinetic energy and time for a particle of mass m released from a height h with zero initial velocity, we can follow these steps:
Step 1: Understand the motion of the particle
The particle is released from rest, so its initial velocity u=0. It falls under the influence of gravity until it strikes the ground. The time taken to fall to the ground can be determined using the equations of motion.
Step 2: Calculate the time to reach the ground
Using the second equation of motion:
s=ut+12at2
where:
- s=h (the height from which it is released),
- u=0 (initial velocity),
- a=g (acceleration due to gravity),
- t=t0 (time taken to reach the ground).
Substituting the values, we have:
h=0⋅t0+12gt20⟹h=12gt20⟹t0=√2hg
Step 3: Calculate the velocity just before impact
Using the first equation of motion:
v=u+at
Substituting the values:
v=0+gt0=g√2hg=√2gh
Step 4: Calculate the kinetic energy just before impact
The kinetic energy KE just before the particle hits the ground is given by:
KE=12mv2=12m(2gh)=mgh
Step 5: Analyze the motion after the impact
Since the collision is elastic, the particle will bounce back with the same speed v=√2gh but in the opposite direction. The time taken to return to the original height h will also be t0.
Step 6: Determine the kinetic energy during the motion
- From t=0 to t=t0: The kinetic energy increases from 0 to mgh.
- From t=t0 to t=2t0: The kinetic energy decreases from mgh back to 0.
Step 7: Plot the graph
- The x-axis represents time t.
- The y-axis represents kinetic energy KE.
- The graph will be a parabola opening upwards, starting from (0,0) to (t0,mgh) and then back to (2t0,0).
Summary of the graph:
- At t=0, KE=0.
- At t=t0, KE=mgh.
- At t=2t0, KE=0.
The particle is released from rest, so its initial velocity u=0. It falls under the influence of gravity until it strikes the ground. The time taken to fall to the ground can be determined using the equations of motion.
Using the second equation of motion:
s=ut+12at2
where:
- s=h (the height from which it is released),
- u=0 (initial velocity),
- a=g (acceleration due to gravity),
- t=t0 (time taken to reach the ground).
h=0⋅t0+12gt20⟹h=12gt20⟹t0=√2hg
Using the first equation of motion:
v=u+at
Substituting the values:
v=0+gt0=g√2hg=√2gh
The kinetic energy KE just before the particle hits the ground is given by:
KE=12mv2=12m(2gh)=mgh
Since the collision is elastic, the particle will bounce back with the same speed v=√2gh but in the opposite direction. The time taken to return to the original height h will also be t0.
- From t=0 to t=t0: The kinetic energy increases from 0 to mgh.
- From t=t0 to t=2t0: The kinetic energy decreases from mgh back to 0.
- The x-axis represents time t.
- The y-axis represents kinetic energy KE.
- The graph will be a parabola opening upwards, starting from (0,0) to (t0,mgh) and then back to (2t0,0).
- At t=0, KE=0.
- At t=t0, KE=mgh.
- At t=2t0, KE=0.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Objective
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A particle of mass m is projected at an angle α to the horizontal with an initial velocity u. The work done by gravity during the time it reaches its highest point is
View SolutionA car is accelerated on a lavelled road and attains a velocity 4 times of its initial velocity. In this process, the potential energy of the car
View Solution
Knowledge Check
A body dropped from a height h with initial velocity zero, strikes the ground with a velocity 3 m/s. Another body of same mass dropped from the same height h with an initial velocity of 4m/s. Find the final velocity of second mass with which it strikes the ground.
A3ms−1B4ms−1C5ms−1D12ms−1A ball falls under gravity from a height of 10 m with an initial downward velocity u. It collides with the ground, losses 50% of its energy in collision and then rises back to the same height. The initial velocity u is
A7ms−1B25ms−1C14ms−1D28ms−1
A particle of mass m is moving along the x-axis with initial velocity ui . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
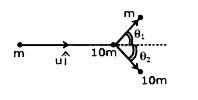
View SolutionA particle is released from height H. At certain height from the ground its kinetic energy is twice its gravitational potential energy. Find the height and speed of particle at that height.
View SolutionA projectill is projected at an angle (α>45∘) with an initial velocity u. The time t, at which its magnitude of horizontal velocity will equal the magnitude of vertical velocity is :-
View SolutionIf a particle is executing S.H.M. then the graph between its acceleration and velocity is , in general
View SolutionA point mass starts moving in a straight line with constant acceleration. After time t0 the acceleration changes its sign, remaining the same in magnitude. Determine the time T from the beginning of motion in which the point mass returns to the initial position.
View SolutionA particle is released from a height S. At certain height its kinetic energy is three times its potential energy. The height and speed of the particle at that instant are respectively
View Solution
